Примеры определения расчетных длин стоек рам

Пример 1. Рассмотрим случаи определения коэффициентов m расчетной длины стоек при предельных значениях п и р.

При п и р, стремящихся к бесконечности, по формулам табл. 27 находим:

а) при р = 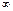и n = 0,2 ;

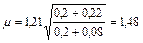б) при р = 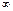и n = 5,0 .

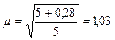При р = 50 и п = 0,2 и п = 5,0 согласно п. 6.10* СНиП II-23-81* получим соответственно m = 1,49 и m = 1,03.

В случае шарнирного закрепления в фундаменте стойки одного яруса рамы рекомендуется пользоваться формулами табл. 27 при р = 0 и n > 0,2. Откуда находим:

а) при р = 0 и n = 1,0 ;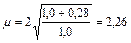

б) при р = 0 и n = .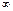

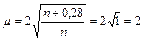Таблица 28

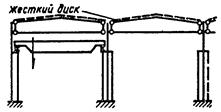
№ п.п.	Конструктивная схема производственного здания	Расчетная схема колонны	Формулы для определения коэффициента m1 нижнего участка колонны	Границы изменения параметров
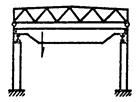
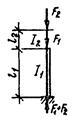
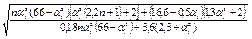
				При a1 £ 1,0 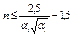; при a1 > 1,2 n £ 1,35 – 0,35 a1
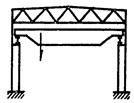
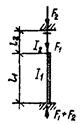
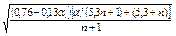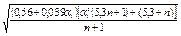
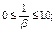
			При a1 £ 1,2 ; при a1 > 1,2	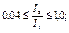0,1 £ m £ 2,0
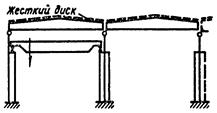
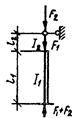
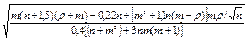
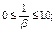
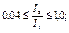
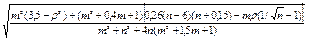
				0,1 £ m £ 2,0

Обозначения, принятые в табл. 28:

; ; ; .

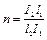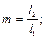
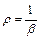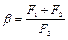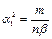Таблица 29

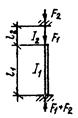
№п.п.	Расчетная схема колонны	Усло­вие нагру­жения колон­ны	Формулы для определения коэффициента m1i нижнего участка колонны
		F2 = 0	m11 = 2,0
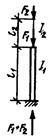
		F1 = 0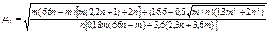
		F2 = 0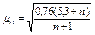
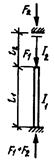
		F1 = 0	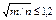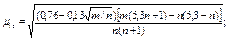При при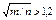
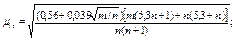
		F2 = 0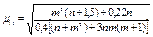
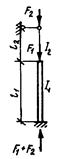
		F1 = 0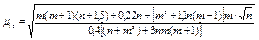
		F2 = 0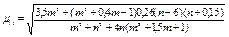
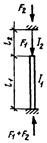
		F1 = 0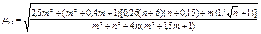

Обозначения, принятые в табл. 29:

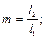
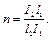
Пример 2. Требуется определить значения коэффициентов расчетной длины m средних колонн многопролетных и многоэтажных зданий.

1. Исходные данные. Двухпролетная одноэтажная рама с жестким закреплением колонн в фундаментах и жестким креплением ригелей к колоннам постоянного сечения. Здесь и далее в примерах принимаем l_r1 = l_r2 = l_r; I_r1 = I_r2 = I_r; (одинаковые пролеты и сечения ригелей); I_r / I_c = 3; l_c / l_r = 0,2;

а) здание, нагруженное силами N во всех узлах по верху колонн.

При k = 2 и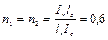

вычислим ;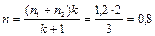

по табл. 17, a СНиП II-23-81*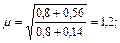

б) здание при неравномерном нагружении узлов в плоскости рамы (одной колонны силой N, а двух других - силами 0,5 N).

По формуле (52) при S a_i = 1 + 0,5 + 0,5 = 2 и S Х_i = 3

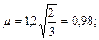
в) здание при наличии продольных связей в конструкции и нагружении в расчетном блоке (из пяти рам) одной колонны в средней раме силой N и двух других колонн в средней раме силами 0,5 N, а остальных колонн в четырех рамах - силами 0,3 N.

Тогда S a_i = 12 × 0,3 + 2 × 0,5 + 1 = 5,6, и S Х_i = 15.

По формуле (52) ;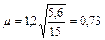

г) здание при нагружении одной колонны в средней раме силой N, двух других колонн силами 0,3 N и всех колонн в оставшихся четырех рамах расчетного блока силами 0,1 N.

При S a_i = 12 × 0,1 + 2 × 0,3 + 1 = 2,8 и S Х_i = 15 по формуле (52) .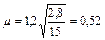

Так как вычисленное m < 0,7, следует принять m = 0,7 (см. поз. 2 табл. 21);

д) конструкция обеспечена от возможности боковой потери устойчивости системы в целом и ее можно отнести к категории несвободной рамы.

При п = 0,8 по формуле (51)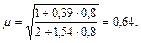

2. Исходные данные. Десятипролетная одноэтажная рама с жестким закреплением колонн в фундаментах и жестким креплением ригелей равных пролетов и сечений к колоннам постоянного сечения нагружена силой N во всех узлах:

а) I_r / I_c = 3; l_c / l_r = 0,2.

При k = 10 и ;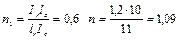

по табл. 17, a СНиП II-23.81*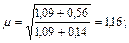

б) I_r / I_c = 3; l_c / l_r = 2.

При k = 10 и ;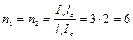

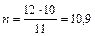по табл. 17, a СНиП П-23-81*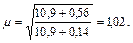

Пример 3. Требуется определить значения коэффициентов m₁ расчетной длины нижнего участка одноступенчатых колонн при различных значениях параметров, приведенных в табл. 28 и 29:

1) для схемы 1 при r = 0,2, m = 2,0, I₂ / I₁ = 0,5, n = 0,25 вычислим 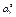= 1,6; при 1,35 – 0,35 a₁ = 0,91 > n по формуле поз. 1 табл. 28 m₁ = 3,28;

2) для схемы 1 при F₁ = 0 и m = 2,0, I₂ / I₁ = 0,5, n = 0,25 вычислим 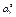= 8,0; при 1,35 - 0,35 a₁ = 0,36 > n по формуле поз. 1 табл. 28 m₁ = 7,15;

3) для схемы 2 при r = 0,2, m = 2,0, I₂ / I₁ = 0,5, n = 0,25 вычислим 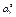= 1,6; при 1,35 – 0,35 a₁ = 0,91 > n по формуле поз. 2 табл. 28 m₁ = 2,12;

4) для схемы 2 при r = 0,8, m = 2,0, I₂ / I₁ = 1,2 > 1, n = 0,6 вычислим 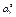= 2,7; при 1,35 - 0,35 a₁ = 0,78 > n по формуле поз. 2 табл. 28 m₁ = 2,59;

5) для схемы 3 при F₂ = 0 и r = 0, т = 2,0; I₂ / I₁ = 0,04, п = 0,02 по формуле поз. 5 табл. 29 m₁ = 1,86;

6) для схемы 3 при F₁ = 0 и r = 1,0, т = 0,1, I₂ / I₁ = 1,0, п = 10,0 по формуле поз. 6 табл. 29 m₁ = 0,77;

7) для схемы 4 при F₂ = 0 и r = 0, т = 2,0, I₂ / I₁ = 0,04, п = 0,02 по формуле поз. 7 табл. 29 m₁ = 1,83;

8) для схемы 4 при F₁ = 0 и r = 1,0, т = 0,1, I₂ / I₁ = 1,0, n = 10,0 по формуле поз. 8 табл. 29 m₁ = 0,55.

6.13 (6.15*). Ограничения гибкостей сжатых стержней вводятся с целью повышения экономичности и надежности стальных конструкций. В определенной мере это реализуется за счет более полного использования прочностных свойств стали как материала, поскольку с увеличением гибкости стержней уровень использования прочности стали уменьшается. Отсюда следует, что применять высокопрочные стали при больших гибкостях экономически нецелесообразно. Ограничения гибкостей способствуют также уменьшению искривлений стержней при изготовлении, транспортировании и Монтаже. Для стержней, сечения которых назначаются по предельным гибкостям, допускается увеличить предельную гибкость в соответствии со СНиП II-23-81*.

Дата добавления: 2014-12-26