
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обчислення площі поверхні обертання
|
|
|
|
Поверхня тіла обертання.
Об'єм тіла обертання
Об’єм тіла обертання.
Нехай навколо осі 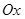 обертається криволінійна трапеція, обмежена неперервною лінією
обертається криволінійна трапеція, обмежена неперервною лінією 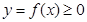 , відрізком
, відрізком  і прямими
і прямими 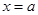 і
і 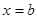 (див. рис. 190). Отримана фігура обертання називається тілом обертання. Перетин цього тіла площиною, перпендикулярною осі
(див. рис. 190). Отримана фігура обертання називається тілом обертання. Перетин цього тіла площиною, перпендикулярною осі 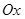 , проведеною через довільну точку
, проведеною через довільну точку 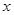 осі
осі 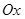 ((
((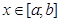 ), є круг з радіусом
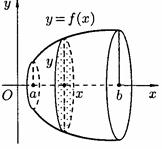
), є круг з радіусом 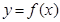 . Отже,
. Отже,  .
.
(рис.190)
Застосовуючи формулу (41.6) об'єму тіла за площею паралельних перетинів, отримаємо
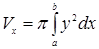 . (9.7.7)
. (9.7.7)
Якщо криволінійна трапеція обмежена графіком неперервної функції 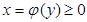 і прямими
і прямими 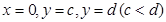 , то об'єм тіла, утвореного обертанням цієї трапеції навколо осі
, то об'єм тіла, утвореного обертанням цієї трапеції навколо осі 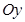 , по аналогії з формулою (9.7.7), дорівнює
, по аналогії з формулою (9.7.7), дорівнює
 . (9.7.8)
. (9.7.8)
Приклад 9.7.7. Знайти об'єм тіла, утвореного обертанням фігури, обмеженої лініями 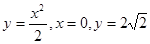 навколо осі
навколо осі 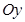 (див. рис.191).
(див. рис.191).

(рис.191)
○ По формулі (9.7.8) знаходимо:
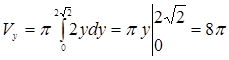 .
.
Нехай крива 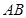 є графіком функції
є графіком функції 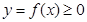 , де
, де 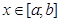 , а функція
, а функція 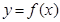 і її похідна
і її похідна 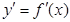 неперервні на цьому відрізку.
неперервні на цьому відрізку.
Знайдемо площу 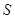 поверхні, утвореної обертанням кривої
поверхні, утвореної обертанням кривої 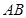 навколо осі
навколо осі 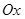 .
.
Застосуємо другу схему (метод диференціала).
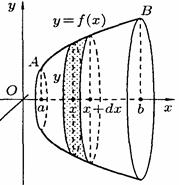
(рис.192)
1. Через довільну точку 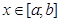 проведемо площину П, перпендикулярну осі
проведемо площину П, перпендикулярну осі 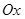 . Площина П перетинає поверхню обертання по колу з радіусом
. Площина П перетинає поверхню обертання по колу з радіусом 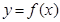 (див. рис. 192).
(див. рис. 192).
Величина 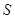 поверхні частини фігури обертання, що лежить лівіше площини, є функцією від
поверхні частини фігури обертання, що лежить лівіше площини, є функцією від 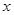 , тобто
, тобто  .
.
2. Дамо аргументу 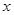 приріст
приріст  . Через точку
. Через точку  також
також
проведемо площину, перпендикулярну осі 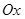 . Функція
. Функція  отримає приріст
отримає приріст  , зображений на рис. виді «поясочка».
, зображений на рис. виді «поясочка».
Знайдемо диференціал площі 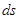 , замінюючи утворену між перетинами фігуру усіченим конусом, твірна якого рівна
, замінюючи утворену між перетинами фігуру усіченим конусом, твірна якого рівна  , а радіуси основ рівні
, а радіуси основ рівні 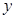 і
і  . Площа його бічної поверхні рівна
. Площа його бічної поверхні рівна 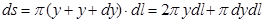 . Відкидаючи добутки
. Відкидаючи добутки  , як нескінченно малу вищого порядку, ніж
, як нескінченно малу вищого порядку, ніж 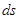 , отримаємо
, отримаємо 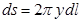 , або, оскільки
, або, оскільки  , то
, то 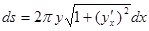 .
.
3. Інтегруючи отриману рівність в межах від 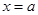 до
до 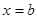 , отримаємо
, отримаємо
 . (9.7.9)
. (9.7.9)
Якщо крива 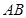 задана параметричними рівняннями
задана параметричними рівняннями  , то формула (9.7.9) для площі поверхні обертання прийме вигляд
, то формула (9.7.9) для площі поверхні обертання прийме вигляд
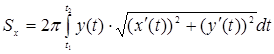 .
.
Приклад 9.7.8. Знайти площа поверхні кулі радіусу  .
.
○ Можна вважати, що поверхня кулі утворена обертанням півкола 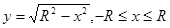 , навколо осі
, навколо осі 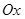 . По формулі (9.7.9) знаходимо
. По формулі (9.7.9) знаходимо
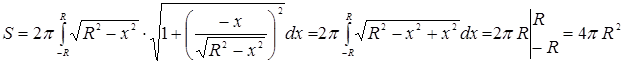 . ●
. ●
Приклад 9.7.9. Дано циклоїда
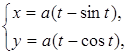
 .
.
Знайти площу поверхні, утвореної обертанням її навколо осі 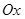 .
.
○ При обертанні половини дуги циклоїди навколо осі 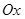 площа поверхні обертання дорівнює
площа поверхні обертання дорівнює
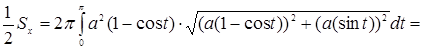


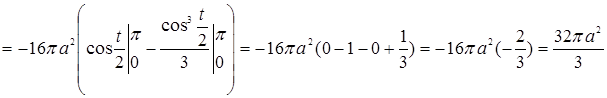 ,
,
тобто  . Отже,
. Отже,  .
.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 7793; Нарушение авторских прав?; Мы поможем в написании вашей работы!