Невласні інтеграли І-го роду

Нехай функція 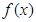неперервна на проміжку 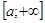. Якщо існує скінчена границя 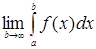, то її називають невласним інтегралом першого роду і позначають .

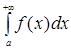Таким чином, по означенню

.

В цьому випадку говорять, що невласний інтеграл 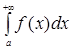збіжний.

Якщо ж вказана границя не існує або вона нескінченна, то говорять, що інтеграл 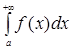розбіжний.

Аналогічно означається невласний інтеграл на проміжку :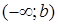

.

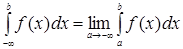невласний інтеграл з двома нескінченними межами визначається формулою , де 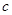— довільне число.

В цьому випадку інтеграл зліва збіжний лише тоді, коли збіжні обидва інтеграли справа. Відзначимо, що якщо неперервна функція 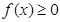на проміжку 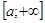і інтеграл 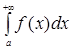збіжний, то він виражає площу нескінченно довгої криволінійної трапеції (див. рис. 172).

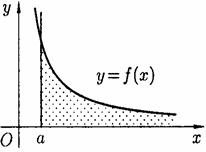
(рис.172)

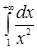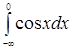Приклад 9.6.1. Обчислити невласні інтеграли або встановити їх розбіжність: 1) ; 2) ; 3) .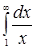

○ 1) 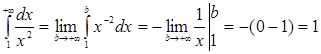, інтеграл збіжний;

2) 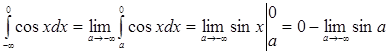, інтеграл розбіжний, оскільки при 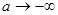границя 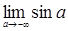не існує.

3) 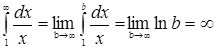, інтеграл розбіжний. ●

В деяких задачах немає необхідності обчислювати інтеграл; достатньо лише знати, чи збіжний він чи ні.

Наведемо без доведення деякі ознаки збіжності.

Дата добавления: 2014-12-26