Методические рекомендации. Вопросы, выносимые на обсуждение

Вопросы, выносимые на обсуждение

1. Интегрирование иррациональных функций, содержащих квадратный трехчлен.

2. Вычисление интегралов вида , , 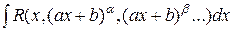, 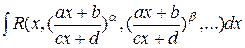где – рациональная функция, , ,… - рациональные числа.

3. Вычисление интегралов , , , .

4. Интегралы от дифференциального бинома 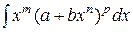, случаи интегрирования в элементарных функциях.

5. Применение подстановок Эйлера при вычислении интегралов .

Для подготовки к занятию дома

1. Выясните, в каких случаях интегралы от иррациональных функций интегрируются в элементарных функциях.

2. Составьте таблицу:

Тип интеграла, содержащего иррациональную функцию	Метод вычисления (указать подстановку и к какому типу интеграла сводится)

3. Изучите разобранные примеры решения типовых задач и законспектируйте их решение в рабочую тетрадь.

На занятии по указанию преподавателя

1. Дайте ответы на вопросы из теоретических заданий для развития и контроля владения компетенциями.

2. В рабочей тетради и на доске решите практические задания для развития и контроля владения компетенциями из заданий, решаемых в аудитории.

Дома закрепите полученные практические умения и навыки, решая практические задания для развития и контроля владения компетенциями из заданий для самостоятельной работы дома.

Рекомендуемая литература

[1] глава 9 п. 9.4.

[2] глава IX § 3.

[3] глава 8 § 41.

[4] часть III занятие 9.

[6] глава 7 § 6.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Найдите следующие интегралы:

1.

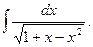
Решение. Этот интеграл содержит корень квадратный из квадратного трехчлена. Преобразуем квадратный трехчлен к виду:

.

Тогда

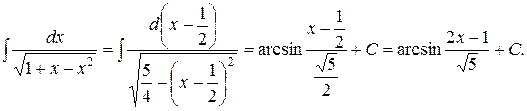
2.

Решение. Выделим в числителе производную подкоренного выражения и разобьем данный интеграл на два интеграла:

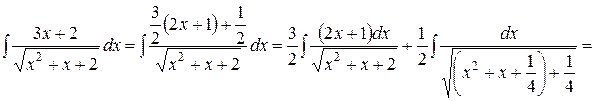
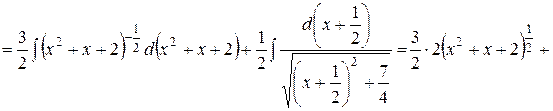
При вычислении полученных интегралов использовали преобразование дифференциала и прием по выделению полного квадрата, рассмотренный в предыдущем примере.

3.

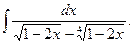
Решение. Сделаем подстановку , тогда 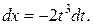В результате получим:

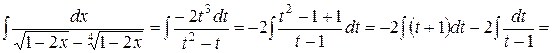
4. .

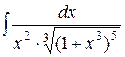Решение. Данный интеграл есть интеграл от дифференциального бинома 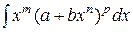, т.е.

, где . Тогда, так как

, то выполняем подстановку 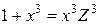. Далее .

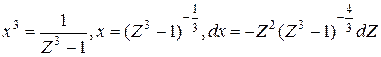Следовательно,

.

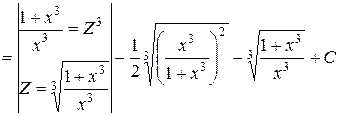5. .

Решение. Данный интеграл можно вычислить с помощью первой подстановки Эйлера:

.

Теоретические задания

Дата добавления: 2014-12-26