Элементы статистической физики, распределения

Примеры решения задач

17. На рисунке приведен график функции распределения некоторой случайной величины x. Считая известной величину a, определить константу A из условия нормировки функции распределения. Вычислить средние значения x и x ².

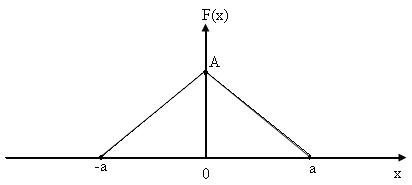
Решение

Знание функции распределения f (x) позволяет найти среднее любой функции F (x) по формуле:

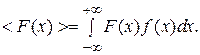(1)

Для определения вида функции распределения необходимо найти константу A. Это можно сделать из условия нормировки функции распределения:

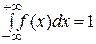. (2)

Из геометрической интерпретации этого интеграла следует, что выражение (2) равно площади под кривой графика функции распределения, т. е. 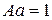. Отсюда для константы A получается: 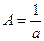. По известной величине A и по графику можно установить аналитический вид функции распределения f (x):

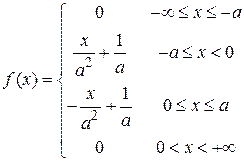. (3)

Из формулы (1) и выражения (3) для средних значений < x > и < x ²> следует:

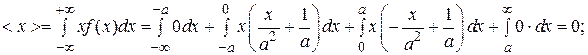
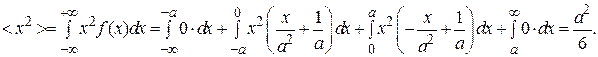
Ответ: ; ; .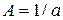

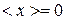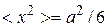18. На какой высоте давление воздуха вдвое меньше, чем на уровне моря?. Температура воздуха T = 290 К.

Дано: 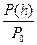= 0,5 T = 290 К μ = 29∙10^-3кг/моль	Решение Зависимость давления P (h) атмосферы с высотой выражается барометрической формулой 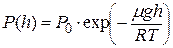, (1) где P 0 – давление на уровне моря; μ – молярная масса воздуха; g – ускорение свободного падения; R – универсальная газовая постоянная.
h –?

Логарифмирование выражения (1) дает 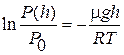. (2)

Из соотношения (2) находим высоту h: .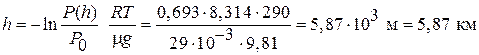

Ответ: h = 5,87 км.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

2.6. На рисунке приведен график функции распределения вероятности

значения некоторой величины x. Найти константу А, при которой функция оказывается нормированной. Вычислить среднее значение x и x ².

О (1/2 a; < x > = 0№ < x ²> = a ²/3)

2.7. Азот находится в равновесном состоянии при Т = 421 К. Определить относительное число D N / N молекул, скорости которых заключены в пределах от 499,9 до 500,1 м/с.

(D N / N = 3,32×10^-4)

2.8. Имеется N частиц, энергия которых может принимать лишь два значения: Е ₁ и Е ₂. Частицы находятся в равновесном состоянии при температуре Т. Чему равна суммарная энергия Е всех частиц в этом состоянии?

(Е = )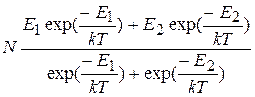

2.9. Пылинки, взвешенные в воздухе, имеют массу m = 1,00×10^{-18 г. Во сколько раз уменьшиться их концентрация n при увеличении высоты на} D h = 10,0 м? Температура воздуха Т = 300 К.

(В e ^23.6 раз)

2.10. В кабине вертолета барометр показывает давление p = 9,00×10⁴ Па. На какой высоте находится вертолет, если на взлетной площадке барометр показывал p ₀ = 1,01×10⁵ Па? Считать, что температура воздуха Т = 290 К не изменяется с высотой.

(h = 890 м)

2.11. На какой высоте давление воздуха составляет 60 % от давления на уровне моря? Температуру воздуха считать постоянной и равной 0° С.

(h = 4.07×10³ м)

Дата добавления: 2014-12-26