
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Электростатика. Диэлектрики
|
|
|
|
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
Примеры решения задач
23. По тонкому кольцу равномерно распределен заряд Q = 40 нКл с линейной плотностью 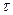 = 50 нКл/м. Определить напряженность
= 50 нКл/м. Определить напряженность 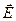 электрического поля, создаваемого этим зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, равное половине радиуса.
электрического поля, создаваемого этим зарядом в точке А, лежащей на оси кольца и удаленной от его центра на расстояние, равное половине радиуса.
Дано:
Q = 40 нКл =  Кл Кл
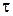 = 50 нКл/м =
= = 50 нКл/м =
= 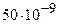 Кл/м
h = Кл/м
h = 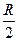
|

|


Напряженность поля, создаваемого этим зарядом 
где  – электрическая постоянная;
– электрическая постоянная;  – единичный вектор, направленный вдоль r. Разложим вектор
– единичный вектор, направленный вдоль r. Разложим вектор  на две составляющие:
на две составляющие:  вдоль оси Z, и
вдоль оси Z, и 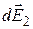 , перпендикулярную оси z,т.е.
, перпендикулярную оси z,т.е.


 .
.
Напряжённость 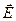 электрического поля в точке А найдём интегрированием
электрического поля в точке А найдём интегрированием

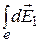
 ,
,
где интегрирование ведется по всем элементам заряженного кольца. Заметим, что для каждой пары зарядов dQ и d 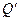 , расположенных симметрично относительно центра кольца, векторы
, расположенных симметрично относительно центра кольца, векторы 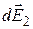 и
и  , в точке А равны по модулю и противоположны по направлению
, в точке А равны по модулю и противоположны по направлению 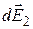 = –
= – 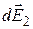 , т.е компенсируют друг друга.
, т.е компенсируют друг друга.
Составляющие  для всех элементов кольца сонаправлены с осью z, т.е.
для всех элементов кольца сонаправлены с осью z, т.е.  =
= 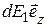 .
.
Тогда 
Так как 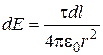 ,
, 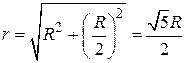 ;
;  , то
, то
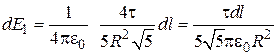 .
.
Таким образом  .
.
Поскольку 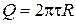 , то радиус кольца
, то радиус кольца 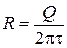 .
.
Тогда  .
.
Значение напряженности на расстоянии z = h = R /2.
 = 7000 В/м = 7,9 кВ/м
= 7000 В/м = 7,9 кВ/м
Ответ: Е = 7,9 кВ/м.
24. Электрическое поле создается бесконечным цилиндром радиусом R, равномерно заряженным с линейной плотность τ. Определите разность потенциалов между двумя точками этого поля, лежащими на расстоянии 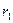 и
и  от поверхности этого цилиндра. Решение
от поверхности этого цилиндра. Решение
 | |||
 | |||
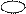       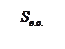  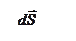      Дано Дано
          R R
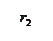      τ τ
    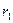
        
|
      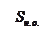 φ1 – φ2 ? φ1 – φ2 ?
|
Интегрирал по гауссовой поверности, верхности раскладываем на три интеграла: по верхнему и нижнему основаниям, по боковой поверхности. Интеграл по верхнему основанию 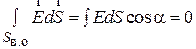 , так как угол
, так как угол 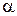 между вектором элементарной площадки
между вектором элементарной площадки  и вектором
и вектором  равен π /2 и cos π /2 = 0. Аналогично для нижнего основания. Остается интеграл по боковой поверхности
равен π /2 и cos π /2 = 0. Аналогично для нижнего основания. Остается интеграл по боковой поверхности  , здесь угол
, здесь угол 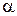 = 0, cos 0 = 1, значение напряженности Е на одном и том же расстоянии r одинаково, Е выносим за знак интеграла
= 0, cos 0 = 1, значение напряженности Е на одном и том же расстоянии r одинаково, Е выносим за знак интеграла 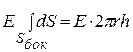 . В правой части теоремы Гаусса заряд, охватываемый гауссовой поверхностью
. В правой части теоремы Гаусса заряд, охватываемый гауссовой поверхностью  . Таким образом, получаем
. Таким образом, получаем

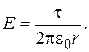
Для нахождения разности потенциалов воспользуемся связью напяженности и потенциала
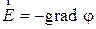 .
.
Для случая радиальной симметрии, реализующейся у нас,
 .
.
Интегрируя это выражение, получим
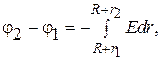 или
или
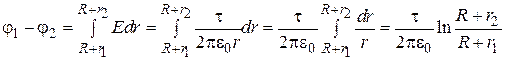 .
.
Ответ:  .
.
25. Плоский конденсатор, между обкладками которого помещена стеклянная пластинка 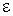 (
(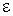 = 6) толщиной l = 2,00 мм, заряжен до напряжения U = 200 В (рис. 1). Пренебрегая величиной заряда между пластинкой и обкладками, найти а) поверхностную плотность
= 6) толщиной l = 2,00 мм, заряжен до напряжения U = 200 В (рис. 1). Пренебрегая величиной заряда между пластинкой и обкладками, найти а) поверхностную плотность 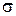 свободных зарядов на обкладках конденсатора, а также б) поверхностную плотность
свободных зарядов на обкладках конденсатора, а также б) поверхностную плотность 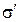 связанных зарядов (зарядов поляризации) на стекле. Изобразить силовые линии электрического поля в стекле и воздушном зазоре между стеклом и обкладками.
связанных зарядов (зарядов поляризации) на стекле. Изобразить силовые линии электрического поля в стекле и воздушном зазоре между стеклом и обкладками.
 Дано: Дано:
U = 200 В | ||
σ –?
σ´ –?
 силовые линии Е силовые линии Е
|
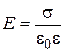 (1)
(1)
Отсюда, учитывая соотношение Е =  , справедливое для однородного поля конденсатора, найдем:
, справедливое для однородного поля конденсатора, найдем:
 (2)
(2)
Чтобы определить величину 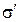 , воспользуемся формулой
, воспользуемся формулой 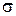 =
= 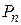 (поверхностная плотность связанных зарядов равна проекции вектора поляризованности
(поверхностная плотность связанных зарядов равна проекции вектора поляризованности  на внешнюю нормаль к поверхности диэлектрика). Так как вектор
на внешнюю нормаль к поверхности диэлектрика). Так как вектор  параллелен вектору напряженности
параллелен вектору напряженности  поля в диэлектрике, направленному по нормали к поверхности стеклянной пластинки, то
поля в диэлектрике, направленному по нормали к поверхности стеклянной пластинки, то 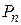 =
=  . Учитывая соотношение
. Учитывая соотношение  = æ
= æ  , где æ – диэлектрическая проницаемость среды и соотношение
, где æ – диэлектрическая проницаемость среды и соотношение 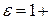 æ, получим:
æ, получим:
 æ
æ 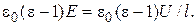 (3)
(3)
Подставляя в формулы (2) и (3) величины в единицах СИ: U = 200 B,  = 2,00
= 2,00  м,
м,  = 8.85
= 8.85 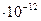 Ф/м, найдем:
Ф/м, найдем:
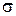 =
= 
 =
= 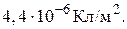
 Чтобы изобразить силовые линии электрического поля в стекле и воздуш ном зазоре, надо помнить, что густота силовых линий пропорциональна напряженности поля, а диэлектрическая проницаемость среды
Чтобы изобразить силовые линии электрического поля в стекле и воздуш ном зазоре, надо помнить, что густота силовых линий пропорциональна напряженности поля, а диэлектрическая проницаемость среды 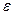 показывает во сколько раз поле внутри диэлектрика слабее поля внутри зазора, следовательно густота силовых линий внутри стеклянной пластинки в шесть раз меньше, чем в зазоре (рис. 2).
показывает во сколько раз поле внутри диэлектрика слабее поля внутри зазора, следовательно густота силовых линий внутри стеклянной пластинки в шесть раз меньше, чем в зазоре (рис. 2).
Ответ: 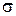 =
= 
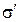 =
= 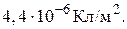
26. Определить дивергенцию следующих векторных полей:
a) 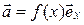 , где f(x) – некоторая функция декартовой координаты х;
, где f(x) – некоторая функция декартовой координаты х;
b) 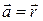 , где
, где  – радиус-вектор точки, в которой определяется дивергенция.
– радиус-вектор точки, в которой определяется дивергенция.
Дано:
а) 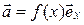 ;
b) ;
b) 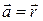
| Решение
По определению
 .
a) .
a) 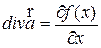 ;
b) Выразим радиус-вектор через компоненты: ;
b) Выразим радиус-вектор через компоненты:
|
div 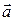 -? -?
|
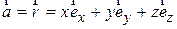 ,
,
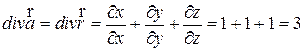 .
.
Ответ:а) 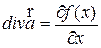 ; b) div
; b) div 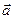 = 3.
= 3.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
3.1. Шар радиусом R заряжен однородно с объёмной плотностью r. Найти напряженность поля  для точек внутри и вне шара.
для точек внутри и вне шара.
( ;
; 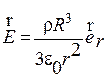 )
)
3.2. Бесконечно тонкая прямая нить заряжена однородно с плотностью l. Найти напряженность электрического поля Е и потенциал j как функции расстояния r от нити. Потенциал на расстоянии r 0 положить равным нулю.
(E = (1/2pe0) l/ r; j = -(l/2pe0) ln (r / r 0))
3.3. Тонкий длинный стержень равномерно заряжен с линейной плотностью t = 1,5 нКл/см. На продолжении оси стержня на расстоянии d = 12 см от его конца находится точечный заряд Q = 0,20 мкКл. Определить силу взаимодействия заряженного стержня и точечного заряда.
(F = 2,2 мН)
3.4. По тонкому проволочному кольцу радиусом r = 60 мм равномерно распределен заряд q = 20 нКл.
а) приняв ось кольца за ось х, найти потенциал j и напряженность поля  на оси кольца как функцию х (начало отсчета х поместить в центр кольца);
на оси кольца как функцию х (начало отсчета х поместить в центр кольца);
б) исследовать случаи х = 0 и ½ х ½>> r.
(E = (1/4pe0)× 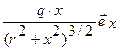 ; j = (1/4pe0)
; j = (1/4pe0)  )
)
3.5. Чему равен поток вектора  через поверхность сферы, внутри объема которой находится:
через поверхность сферы, внутри объема которой находится:
а) заряд е;
б) заряд - е;
в) диполь с моментом  ?
?
Объясните результат с помощью картины силовых линий электрического поля.
3.6. Металлический шар радиусом R помещен в однородное электрическое поле. Изобразите качественную картину силовых и эквипотенциальных линий электрического поля.
3.7. Два точечных заряда +е и - е расположены в точках с координатами (а /2,0,0), (-а /2,0,0). Построить качественно график зависимости проекции напряженности поля Ех (х) для точек, лежащих на оси х (у = 0).
3.8. Найти зависимость плотности зарядов от декартовых координат ρ(x, y, z), при которой напряженность поля описывалась бы функцией 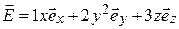 (В/м).
(В/м).
(ρ(x, y, z) = 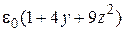 Кл/м3)
Кл/м3)
3.9. Потенциал поля, создаваемого некоторой системой зарядов, имеет вид: j = a (x 2+ y 2)- bz 2, где а и b – положительные константы. Найти напряженность поля Е и ее модуль ½ Е ½. Построить графики зависимости Ex = f (x), Ez = f (z).
(E = 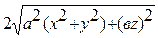 ;
; 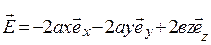 )
)
3.10. Плоский воздушный конденсатор подключили к батарее, а затем отключили от неё. После этого уменьшим расстояние между пластинами конденсатора в 2 раза. Как изменится:
а) энергия, запасенная конденсатором;
б) заряд на обкладках конденсатора;
в) плотность энергии электрического поля конденсатора?
3.11. Диэлектрическая пластина шириной 2 а с проницаемостью e = 2 помещена в однородное электрическое поле напряженности Е, силовые линии которого перпендикулярны пластине.
а) изобразите на рисунке линии полей Е и D электрического поля;
б) постройте качественно графики зависимостей Ех, Dх от х (ось х перпендикулярна пластине, вектор Е направлен вдоль оси х, точка х = 0 находится в середине пластины).
3.12. Диэлектрическая пластинка с проницаемостью e = 2 помещена в однородное электрическое поле с напряженностью Е. Линии поля Е образуют некоторый угол j с поверхностью пластины. Изобразите качественно линии полей Е и D в вакууме и в пластине. Постройте качественно графики зависимостей Еx = f (x) и Dx = f (x).
3.13. Внутри плоской однородной диэлектрической пластины с e = 3 вектор напряженности однородного электрического поля составляет угол j с поверхностью пластины. Считая, что с одной стороны пластины вакуум, а с другой стороны диэлектрик с e = 2, изобразить качественно линии Е и D электрического поля в трех указанных средах. Построить качественно зависимости Еx = f (x) и Dx = f (x). Ось ОХ перпендикулярна поверхностям пластины, а ее толщина d.
3.14. Плоский воздушный конденсатор опустили в воду так, что поверхность воды параллельна плоскостям пластин, а ее уровень расположен на расстоянии h от нижней пластины. Найти зависимость электроемкости конденсатора от величины h, если площадь пластины S, а расстояние между ними d.
(С = 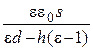 )
)
3.15. Электрическое поле создается равномерно заряженным шаром радиусом R с объемной плотностью заряда r. Определить зависимость вектора электрического смещения электрического поля от r. Построить качественно график D = f (r).
(D = (1/3)r r; D = (r/3)×(R 3/ r 2))
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 2069; Нарушение авторских прав?; Мы поможем в написании вашей работы!
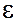 =
=  , с учетом наличиия диэлектрика
, с учетом наличиия диэлектрика
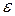 = 6,0
= 6,0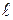 = 2,00 мм
= 2,00 мм