
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Механические колебания и волны. Пример решения задачи
|
|
|
|
Пример решения задачи
35. Вдоль шнура распространяется поперечная волна, уравнение которой имеет вид 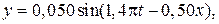 м, где
м, где 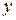 – смещение точек шнура;
– смещение точек шнура;  – время, с;
– время, с; 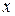 – координата точек шнура, м.
– координата точек шнура, м.
Найти: а) период колебания точек шнура 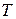 ; б) скорость распространения волны
; б) скорость распространения волны  ; в) длину волны
; в) длину волны 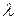 ; г) разность фаз колебаний
; г) разность фаз колебаний  точек шнура, находящихся на расстоянии
точек шнура, находящихся на расстоянии 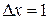 м; д) амплитуду скорости
м; д) амплитуду скорости  поперечного движения частиц шнура.
поперечного движения частиц шнура.
Дано:
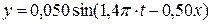 м м
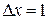 ,0 м ,0 м
| Решение Как известно, уравнение поперечной плоской волны, распространяющейся вдоль оси Х, имеет вид: |
а) 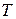 -?; б) -?; б)  –? в) –? в) 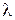 –?;
г) –?;
г)  –?; д) –?; д)  –? –?
|  , (1) , (1)
|
где 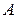 - амплитуда смещения,
- амплитуда смещения, 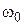 – циклическая частота,
– циклическая частота, 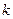 – волновое число,
– волновое число, 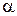 – начальная фаза. Из сравнения условий задачи и выражения (1) можно найти искомые величины.
– начальная фаза. Из сравнения условий задачи и выражения (1) можно найти искомые величины.
Период колебания 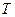 вязан с циклической частотой соотношением:
вязан с циклической частотой соотношением:
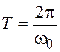 . Поэтому
. Поэтому  с.
с.
Волновое число определяется выражением 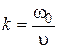 .
.
Поэтому для скорости распространения волны  имеем
имеем
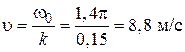
По найденным значениям периода колебаний  и скорости волны
и скорости волны  можно определить длину волны из соотношения
можно определить длину волны из соотношения 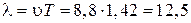 м.
м.
Разность фаз колебаний любых двух точек шнура определяется формулой
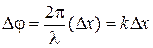 .
.
Поэтому для точек шнура из условия задачи имеем
 рад.
рад.
Скорость смещения точек шнура в поперечном направлении получается дифференцированием по времени выражения (1), т.е.
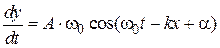 (2)
(2)
Из условия задачи и формулы (2) для максимального значения скорости 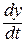 получается:
получается: 
Ответ: а)  с; б)
с; б) 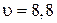 м/с; в)
м/с; в)  м; г)
м; г) 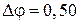 рад; д)
рад; д) 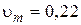 м/с.
м/с.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
4.1. Найти смещение от положения равновесия точки, отстоящей от источника колебаний на расстояние l = l/12, для момента времени t = T /6. Амплитуда колебания А = 0,050 м.
(0,043 м)
4.2. Амплитуда гармонического колебания 5,0 см, период 4,0 с. Найти максимальную скорость колеблющейся точки и ее максимальное ускорение.
(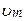 = 7,8·10-2 м/с; am = 0,12 м/с2)
= 7,8·10-2 м/с; am = 0,12 м/с2)
4.3. Уравнение плоской волны имеет вид y = 0,34×cos(0,20 t – 0,40 x), где y – смещение частиц среды, и все числовые значения заданы в системе СИ. Записать числовые значения частоты и периода колебаний, волнового числа, фазовой скорости и длины волны, а также максимальное значение смещения.
( = 0,50 м/с; l = 16 м)
= 0,50 м/с; l = 16 м)
4.4. Поперечная волна распространяется вдоль упругого шнура со скоростью  = 15 м/с. Период колебания точек шнура Т = 1,2 с. Определить разность фаз Dj колебаний двух точек, лежащих на луче и отстоящих от источника волн на расстояниях x 1 = 20 м, x 2 = 30 м.
= 15 м/с. Период колебания точек шнура Т = 1,2 с. Определить разность фаз Dj колебаний двух точек, лежащих на луче и отстоящих от источника волн на расстояниях x 1 = 20 м, x 2 = 30 м.
(200°)
4.5. Материальная точка совершает гармонические колебания согласно уравнению 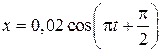 м. Определить: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу; 4) максимальную скорость точки; 5) максимальное ускорение; 6) через сколько времени после начала отсчета точка будет проходить положение равновесия.
м. Определить: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу; 4) максимальную скорость точки; 5) максимальное ускорение; 6) через сколько времени после начала отсчета точка будет проходить положение равновесия.
(Т = 2 с; 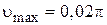 м/c;
м/c; 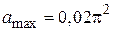
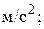
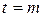
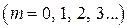 )
)
4.6. Период затухающих колебаний Т = 4,0 с; логарифмический декремент затухания 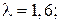 начальная фаза
начальная фаза  При t = T /8 смещение точки х = 4,5 см. Написать уравнение этого колебания. Построить график этого колебания в пределах двух периодов.
При t = T /8 смещение точки х = 4,5 см. Написать уравнение этого колебания. Построить график этого колебания в пределах двух периодов.
(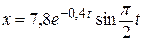 см)
см)
4.7. Поперечная волна, распространяясь вдоль упругого шнура, описывается уравнением 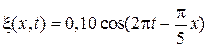 м. Определите: длину волны, фазу колебаний, смещение, скорость и ускорение точки, расположенной на расстоянии
м. Определите: длину волны, фазу колебаний, смещение, скорость и ускорение точки, расположенной на расстоянии  = 9 м от источника колебаний в момент времени
= 9 м от источника колебаний в момент времени 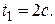 (
(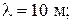
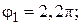
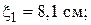

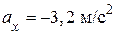 )
)
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 788; Нарушение авторских прав?; Мы поможем в написании вашей работы!