
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Магнетизм. Примеры решения задач
|
|
|
|
Примеры решения задач
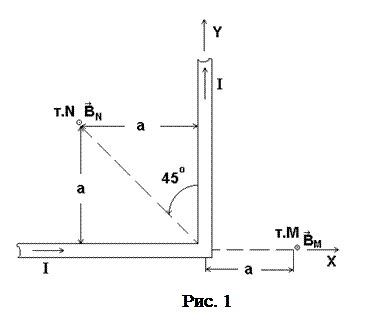 31. Бесконечно длинный прямой проводник согнут под прямым углом, как показано на рис. 1. По проводнику течет ток
31. Бесконечно длинный прямой проводник согнут под прямым углом, как показано на рис. 1. По проводнику течет ток  А. Найти магнитную индукцию
А. Найти магнитную индукцию 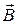 в точках М и N, если
в точках М и N, если 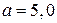 см.
см.
Дано:
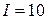 А А
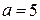 ,0 см = 5,0×10-2 м ,0 см = 5,0×10-2 м
| Решение
Величина магнитной индукции 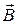 в точках М и N может быть найдена по принципу суперпозиции: в точках М и N может быть найдена по принципу суперпозиции:
|
а) 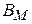 –?
б) –?
б) 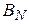 –? –?
| 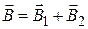 , (1) , (1)
|
 где
где  – магнитная индукция от полубесконечной части проводника, лежащей вдоль оси Х;
– магнитная индукция от полубесконечной части проводника, лежащей вдоль оси Х; 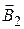 – магнитная индукция от полубесконечной части проводника, лежащей вдоль оси Y. Модуль вектора магнитной индукции может быть рассчитан на основе закона Био – Савара – Лапласа. Нас интересует и будет использоваться результат расчета для прямолинейного отрезка проводника, представленного на рис. 2. Модуль вектора магнитной индукции в точке А на расстоянии b от отрезка проводника выражается формулой
– магнитная индукция от полубесконечной части проводника, лежащей вдоль оси Y. Модуль вектора магнитной индукции может быть рассчитан на основе закона Био – Савара – Лапласа. Нас интересует и будет использоваться результат расчета для прямолинейного отрезка проводника, представленного на рис. 2. Модуль вектора магнитной индукции в точке А на расстоянии b от отрезка проводника выражается формулой
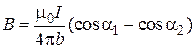 , (2)
, (2)
где 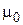 – магнитная постоянная,
– магнитная постоянная, 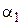 и
и 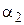 – углы между направлениями тока и направлениями радиус-векторов
– углы между направлениями тока и направлениями радиус-векторов 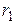 и
и 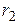 – начала и конца отрезка (см. рис. 2).
– начала и конца отрезка (см. рис. 2).
В точке М (см. рис. 1) вклад в величину магнитной индукции от полубесконечной части проводника, лежащей вдоль оси Х, равен нулю (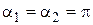 ). Вклад в величину магнитной индукции от полубесконечной части проводника, лежащей вдоль оси Y, характеризуется углами
). Вклад в величину магнитной индукции от полубесконечной части проводника, лежащей вдоль оси Y, характеризуется углами 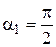 и
и 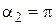 . Поэтому, как это следует из формул (1) и (2), модуль вектора магнитной индукции
. Поэтому, как это следует из формул (1) и (2), модуль вектора магнитной индукции  в точке М:
в точке М:
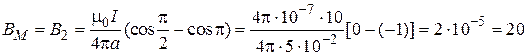 мкТл.
мкТл.
Направление вектора 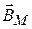 определяется правилом правого винта и показано на рис. 1.
определяется правилом правого винта и показано на рис. 1.
В точке N, как это следует из правила правого винта, вектора  и
и 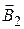 направлены вдоль одной линии перпендикулярно плоскости рис. 1. Поэтому модуль вектора магнитной индукции в точке N равен сумме модулей векторов
направлены вдоль одной линии перпендикулярно плоскости рис. 1. Поэтому модуль вектора магнитной индукции в точке N равен сумме модулей векторов 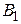 и
и 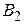 . Для величины магнитной индукции
. Для величины магнитной индукции 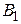 , как следует из рис. 1, угол
, как следует из рис. 1, угол 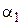 равен нулю, а угол
равен нулю, а угол  . Для величины
. Для величины 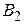 магнитной индукции, как следует из рис.1, угол
магнитной индукции, как следует из рис.1, угол 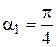 , а угол
, а угол 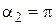 . Поэтому, как это следует из формул (1) и (2), модуль вектора магнитной индукции
. Поэтому, как это следует из формул (1) и (2), модуль вектора магнитной индукции 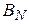 в точке N равен:
в точке N равен:
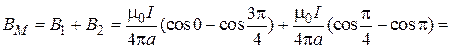
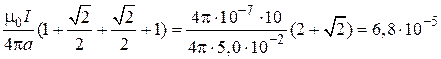 Тл
Тл 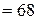 мкТл.
мкТл.
Направление вектора 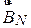 определяется правилом правого винта и показано на рис.1.
определяется правилом правого винта и показано на рис.1.
Ответ: а)  мкТл; б)
мкТл; б)  мкТл.
мкТл.
32. Тонкое кольцо радиусом 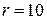 см заряжено равномерно с линейной плотностью заряда
см заряжено равномерно с линейной плотностью заряда 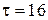 нКл/м. Кольцо вращается с частотой
нКл/м. Кольцо вращается с частотой 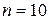 об/c. относительно оси, перпендикулярной плоскости кольца и проходящей через его центр. Определить магнитный момент
об/c. относительно оси, перпендикулярной плоскости кольца и проходящей через его центр. Определить магнитный момент 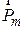 , обусловленный вращением кольца.
, обусловленный вращением кольца.
Дано:
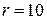 см см
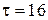 нКл/м нКл/м
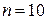 об/c об/c
| Решение: Вращение заряженного кольца представляет собой круговой ток. Круговой ток создает в пространстве магнитный момент, величина модуля которого определяется выражением: |
 –? –?
|  , ,
|
где 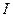 – сила кругового тока;
– сила кругового тока; 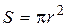 – площадь контура (кольца).
– площадь контура (кольца).
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 1291; Нарушение авторских прав?; Мы поможем в написании вашей работы!