Аппарат дисперсионного анализа

1. Рассмотрим структуру эффектов однофакторной схемы (2.1.3) (эффект 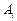и ошибку 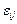). Для эффекта 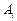, согласно (2.1.2), очевидно соотношение

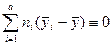. (2.2.1)

Для двух других отклонений справедливы аналогичные соотношения:

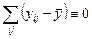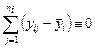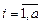, , . (2.2.2)

Рассмотрим сумму квадратов отклонений 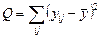. Произведя то же самое действие с правой частью (2.1.3), получим

.

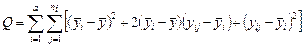Суммируя почленно, будем иметь

;

.

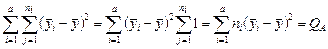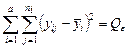Суммируя оставшиеся слагаемые, получаем

,

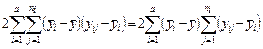откуда, на основании (2.2.1), (2.2.2), получаем тождественный ноль. Так, приходим к тождеству 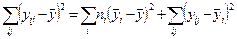, или, в принятых обозначениях:

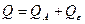. (2.2.3)

Полученное соотношение (2.2.3) носит название основное уравнение дисперсионного анализа. Каждая из компонент суммы квадратов имеет число степеней свободы, как было показано в п.1.4, равное количеству независимых нормальных СВ (совокупности, из которых получены групповые выборки, априорно полагаются нормальными). Для определения числа степеней свободы существует простое мнемоническое правило:

число степеней свободы = количество слагаемых в связывающей их сумме – количество уравнений.

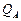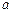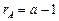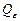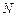Для суммы квадратов эффекта имеем слагаемых и одно уравнение (2.2.1). Следовательно, число степеней свободы составит . У суммы квадратов случайной ошибки на слагаемых приходится 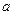уравнений (2.2.2) (по количеству групп). Число ее степеней ошибки 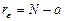. И, наконец, для полной суммы на 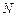слагаемых приходится одно уравнение (первое (2.2.2)). Таким образом, приходим к следующему очевидному тождеству (используемому в практике дисперсионного анализа в качестве одной из операций проверочного расчета):

.

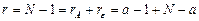Таким образом, численной мерой изменчивости отклика служит сумма квадратов отклонений Q, которая, как гласит основное уравнение дисперсионного анализа, может быть представлена в виде суммы парциальных сумм квадратов Q _A+ Q _e – компонент, характеризующих вклад в полную изменчивость отклика каждого из источников изменчивости. Однако непосредственное сравнение величин Q _A и Q _e не позволяет сделать обоснованный вывод о том, какой из источников является более значимым (весомым). Поскольку у каждой компоненты свое число степеней свободы, то представляется естественным сравнивать между собой средние квадраты отклонений (на одну степень свободы):

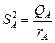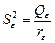, . (2.2.4)

При этом вполне очевидно, что методика сравнения (оценки значимости эффекта фактора) должна строиться исходя из вероятностного содержания основных исходных допущений (о нормальности и взаимной независимости всех индивидуальных значений). Единственно возможным в данной ситуации представляется использование аппарата дисперсионного анализа, конечно, если сами исходные данные не находятся в явном противоречии с теми самыми исходными допущениями.

2. В предыдущем пункте путем простых рассуждений было установлено, что численной мерой, характеризующей каждый из источников изменчивости, является средний квадрат отклонения и обоснована применимость дисперсионного анализа. Вероятностное содержание исходных допущений при более детальном рассмотрении заключается в наличии всего двух альтернативных гипотез:

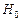· – все групповые выборки получены из одной нормальной совокупности;

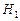· (альтернатива) – групповые выборки получены из нормальных совокупностей с одной генеральной дисперсией, но с разными генеральными средними.

По существу, все проблемы дисперсионного анализа, так или иначе, вращаются вокруг этих двух альтернатив. При этом к формулировке гипотезы 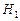следует сделать небольшое уточнение:

1) очевидно, что она (вместе с 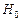) вложена в общую гипотезу о нормальности и постоянстве генеральной дисперсии. Сама же эта внешняя гипотеза непосредственно в дисперсионном анализе не проверяется.

2) поскольку 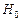и 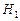образуют полную группу внутри общей внешней гипотезы, правильнее было бы сказать: «не все генеральные средние групповых выборок равны между собой».

Для уяснения «механизма» использования дисперсионного анализа найдем МО средних квадратов (2.2.4) для каждой из гипотез. Для 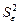будем иметь

.

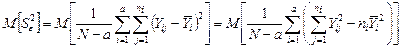Используя свойство МО (п.1.1), последнее соотношение преобразуем к виду

.

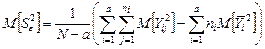Далее, используя соотношение для дисперсии, получим

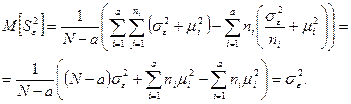
Данное тождество было получено применительно к условиям 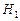. Очевидно, что оно справедливо и для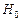 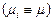. Таким образом, приходим к выводу, что 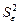является несмещенной оценкой генеральной дисперсии (дисперсии случайной ошибки) .

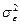Теперь найдем МО 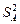для :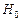

.

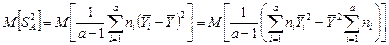Применяя аналогичную последовательность преобразований и учитывая, что 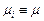, получаем

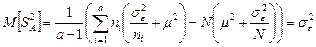. (2.2.5)

Таким образом, можно считать доказанной теорему Фишера, которую в контексте предыдущего изложения можно сформулировать так:

При справедливости гипотезы 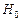средние квадраты эффекта и ошибки есть несмещенные оценки генеральной дисперсии ошибки .

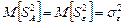Отсюда следует, что отношение средних квадратов есть рассмотренное в п.1.2 дисперсионное отношение Фишера:

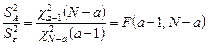. (2.2.6)

Здесь следует сделать следующее замечание. Закону Фишера будет (в рамках 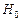) подчиняться и обратное отношение:

.

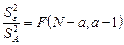Однако практический интерес представляет лишь ситуация 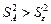, и поскольку исторически сложилась практика оценки правдоподобия 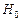по верхней 5% точке, т.е. когда 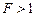, в литературе дисперсионное отношение фигурирует в виде (2.2.6). Возможно будет уместным замечание более общего характера о том, что в любом прикладном статистическом анализе никогда не следует отождествлять объект исследования с априорными вероятностными схемами, положенными в основу модели. В противном случае, как это не парадоксально звучит, в погоне за точностью можно не только потерять адекватность модели, но и вовсе прийти к абсурдным результатам и выводам. Впрочем, при ближайшем рассмотрении, никакого парадокса здесь нет, и это обстоятельство является естественным следствием специфики стохастических закономерностей.

Для МО 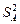при справедливости 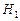по аналогии получим:

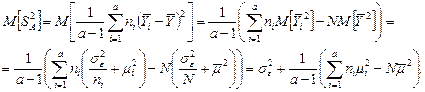
В последнем выражении общее генеральное среднее 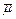находим по правилу суперпозиции (п.1.2):

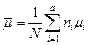. (2.2.7)

В результате после элементарных преобразований окончательно получаем

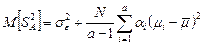, (2.2.8)

где 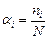- парциальная доля 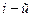группы. Сумму во втором слагаемом (2.2.8) естественно интерпретировать как «дисперсию эффекта фактора»:

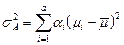. (2.2.9)

Несмещенная оценка этой компоненты дисперсии согласно (2.2.8) будет иметь вид

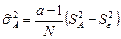. (2.2.10)

Таким образом, доказана теорема Эрвина о выделении эффекта фактора, и алгоритм дисперсионного анализа в простейшем однофакторном случае заключается в следующем:

1) вычисляются средние квадраты , ;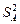

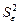2) вычисляется их отношение 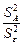и сравнивается с правой 5% точкой статистики Фишера – с квантилью 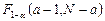. Если выполняется условие 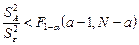, то 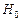принимается как правдоподобная (генеральные средние групповых выборок равны между собой ~ эффект фактора отсутствует). При этом наилучшей оценкой генеральной дисперсии ошибки будет средневзвешенный средний квадрат:

;

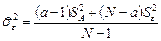3) если 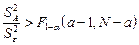, то более правдоподобной признается альтернативная гипотеза 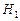. Соответственно ряд групповых средних признается неоднородным, что эквивалентно значимости эффекта фактора.

3. Изложенные в предыдущем пункте результаты и методика легко обобщаются на случай двух и большего числа факторов. Наибольшую сложность и, соответственно, интерес представляет переход от однофакторной к двухфакторной схеме. Пусть факторы 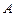и 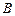варьируются на 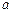и 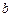уровнях соответственно. В каждой из 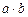элементарных ячеек содержится 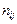индивидуальных значений отклика. В дальнейшем, чтобы избежать громоздких формул, примем непринципиальное ограничение 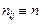. Каждое индивидуальное значение теперь будет иметь 3 индекса: 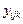, где 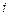- номер уровня фактора 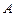; 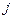- фактора 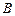; 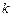- порядковый номер внутри ячейки. Как и в однофакторном случае, средний результат по ячейке 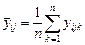дает оценку отклика на пересечении уровне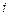й и 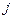. Смысл средних по уровням каждого фактора вполне очевиден из их определения:

; .

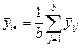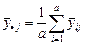Точками условимся обозначать индексы, исчезающие при повышении порядка усреднения. Принимая за начало отсчета общий средний результат

,

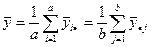соотношения для эффектов получим в виде:

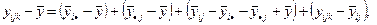(2.2.11)

где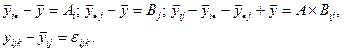

Соотношение (2.2.11), являющееся очевидным тождеством, содержит уже 4 источника изменчивости. Принципиальным отличием двухфакторной схемы является наличие третьего слагаемого в (2.2.11) – так называемого взаимодействия факторов. Первые два называются главными эффектами факторов. Последнее, как и в предыдущем случае, ошибка эксперимента. Для лучшего уяснения смысла вновь возникшего феномена – (А × В) - взаимодействия – следует сделать небольшое отступление.

Факторы 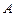и 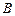априорно независимы. Поэтому термин эффект взаимодействия звучит на первый взгляд несколько странно. Взаимодействие факторов проявляется в том, что при варьировании одного фактора отклик меняется по-разному в зависимости от уровня второго фактора.

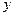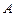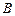Наглядно это можно легко себе представить на простом модельном примере. Пусть - выход продукта, а и соответственно давление и температура в реакторе. Пусть, для простоты, каждый фактор варьируется всего на двух уровнях.

Изобразим графически зависимость 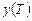, а 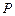интерпретируем как параметр.

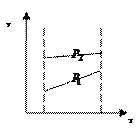
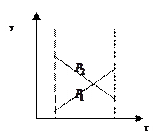
а б в

Рис. 2.2.1. Схема двухфакторного взаимодействия

На рис. 2.2.1 а,б 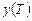изменяется одинаково (или почти одинаково) на обоих уровнях 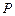, что свидетельствует об отсутствии значимого взаимодействия (если и есть, то слабое). В варианте рис. 2.2.1 в картина принципиально иная. Здесь налицо явные признаки значимого взаимодействия. То же самое будет наблюдаться в координатах 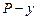, когда 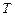будет служить параметром.

При большем числе факторов геометрическую интерпретацию дать уже невозможно, но «механизм» взаимодействия будет тем же самым.

Возвращаясь к схеме дисперсионного анализа, возведем обе части (2.2.11) в квадрат и просуммируем по всем , , :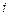

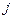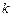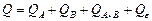, (2.2.12)

где частичные суммы соответственно равны:

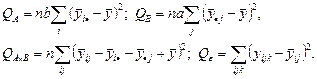(2.2.13)

Вывод (2.2.12) не содержит ничего принципиально отличающегося от (2.2.3): перекрестные произведения при суммировании обнуляются, а это, в свою очередь, напрямую вытекает из соотношений, аналогичных (2.2.1), (2.2.2). Число степеней свободы каждой частичной суммы определяется, как и в однофакторной схеме: количество слагаемых, входящих в сумму, – количество уравнений – связей. Для 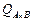при фиксированном 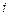получим 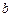уравнений. Добавляя к ним оставшиеся 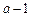уравнений, образующихся при других значениях 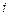и фиксированном 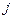, получаем 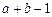уравнений. Таким образом, для взаимодействия число степеней свободы составит:

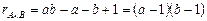. (2.2.14)

Для остальных компонент соотношение очевидно, и получаем

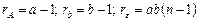. (2.2.15)

Далее, как и в однофакторной схеме, находим средние квадраты отклонений:

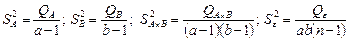. (2.2.16)

Значимость каждого из трех источников контролируемой изменчивости оценивается по величине дисперсионного отно- шения .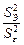

4. При увеличении количества факторов соотношения, аналогичные (2.2.11) 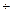(2.2.13), остаются справедливыми. Основное отличие заключается в том, что резко возрастает количество взаимодействий высших порядков. В силу коммутативности взаимодействий 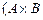~ 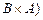количество взаимодействий кратности 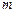в 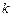-факторном эксперименте составит 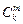. Парных взаимодействий будет 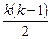, тройных 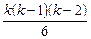и т.д. Таким образом, структу-
ра эффектов трехфакторного эксперимента будет содержать три главных эффекта, три парных взаимодействия, одно тройное и ошибку:

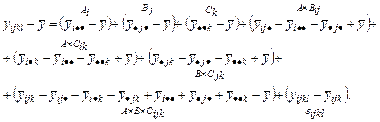(2.2.17)

Частичные суммы квадратов и числа степеней свободы составят соответственно:

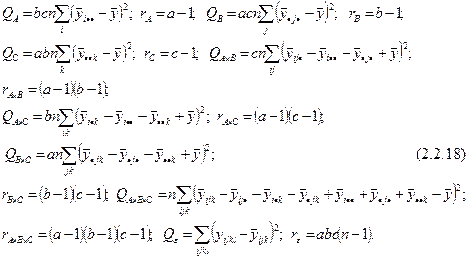
Значимость каждого из 7 источников контролируемой изменчивости оценивается точно так же по величине дисперсионного отношения .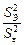

5. Одной из важнейших задач дисперсионного анализа является ранжирование значимых источников изменчивости. По завершении процедуры собственно дисперсионного анализа значимыми признаются только те эффекты и взаимодействия, у которых средние квадраты значительно превышают средний квадрат случайной ошибки (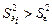), а остальные смешиваются со случайной ошибкой так же, как в однофакторной схеме. При этом в качестве более правдоподобной принимается альтернатива 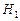, и несмещенной оценкой соответствующей компоненты дисперсии (парциальной дисперсии) является 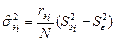. В сущности говоря, этот факт есть прямое следствие правила вычисления дисперсии суперпозиции (вероятностной смеси) СВ, рассмотренного в п.1.2. Оценкой дисперсии полной изменчивости будет сумма всех парциальных дисперсий, включая дисперсию случайной ошибки:

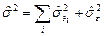, (2.2.19)

где 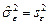. Ранжировать эффекты и взаимодействия, признанные значимыми по результатам эксперимента, целесообразно по величине удельной доли соответствующей парциальной дисперсии:

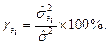(2.2.20)

Именно на основании полученного по (2.2.19), (2.2.20) числового ряда и делаются выводы об объекте исследования в знакомой всем формулировке примерно такого содержания: «… продолжительность жизни на 30% определяется чистотой воздушной среды, на 20% - качеством потребляемой питьевой воды и т.д. …».

Дата добавления: 2014-12-26