Модель функционирования системы контроля

И измерительных процессов

1. Общая постановка задачи выборочного контроля в простейшем варианте одинарной выборки заключается в следующем. Объектом контроля является партия, содержащая N изделий или полуфабрикатов (единиц продукции). Каждая единица продукции в результате контрольной процедуры может быть однозначно отнесена к одной из двух категорий: годная (соответствующая) или негодная (несоответствующая). Из партии методом случайного отбора извлекается безвозвратная выборка объемом n < N, и по результатам контроля выбранных n единиц выносится заключение о качестве не- проконтролированного остатка партии в количестве N – n единиц. Заключение о качестве партии, в конечном счете, сводится к одной из двух альтернатив: партия либо принимается по выборке, либо отклоняется (бракуется). В последнем случае, в принципе, возможны также две альтернативы: возврат поставщику, либо разбраковка (сплошной контроль остатка партии). В дальнейшем ограничимся только рассмотрением этапа принятия решения по выборке, то есть приемка либо браковка предъявленной партии по результатам контроля единиц продукции, попавших в выборку. Для применения к такой контрольной процедуре аппарата теории вероятностей, очевидно, необходимо установить однозначные критерии принятия решения и годности партии. Такими критериями являются: число дефектных единиц в выборке d и предельно допустимое число дефектных единиц в партии D. То есть, если в предъявленной партии содержится не более чем D дефектных единиц, то она считается пригодной для использования по назначению (в противном случае – нет), и соответственно, если при контроле обнаружено не более чем d дефектных изделий, партия принимается. В противном случае бракуется. При этом очевидно, что поскольку фактическое число дефектных единиц в партии, точнее говоря в непроконтролированном остатке, в результате выборочного контроля остается неизвестным, то существует возможность ошибочных решений.

Можно напрасно забраковать годную партию (ошибка 1 рода, вероятность которой принято называть 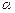- риском), либо с вероятностью 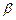( 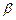- риск) принять несоответствующую партию. Таким образом, в терминах вероятностной схемы приходим к следующей системе СВ: - число дефектных единиц в предъявленной партии – целочисленная СВ с множеством возможных значений ; 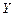- число дефектных единиц в выборке – целочисленная СВ с возможными значениями 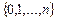; 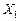- число дефектных единиц в принятой партии с возможными значениям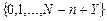и ; - число дефектных единиц в забракованной партии - .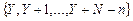

Каждая из СВ имеет свой ряд распределения, причем 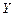в результате контроля принимает определенное значение, а относительно , , 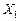можно оперировать лишь оценками правдоподобия двух альтернативных гипотез: 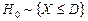, . Пусть принимает фиксированное значение: . Тогда априорное условное распределение 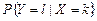, поскольку выборка бесповторная представляет собой закон «Спортлото»:

, . (3.1.1)

Частичная сумма ряда (3.1.1) для l =0,..., d называется оперативной характеристикой контрольного плана:

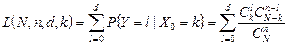. (3.1.2)

Сам же контрольный план (в простейшем случае одинарной выборки) полностью характеризуется тройкой чисел (N,n,d). Оперативная характеристика (3.1.2) однозначно определяет вероятность приемки партии в зависимости от числа дефектных единиц в предъявленной партии k. В литературе и нормативных документах, посвященных вопросам выборочного контроля, 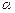- и 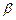- риски устанавливаются непосредственно по оперативной характеристике. Это связано с тем, что априорный безусловный закон , как правило, неизвестен. Однако следует иметь в виду, что задание одной только оперативной характеристики и определяемых по ней априорных рисков само по себе никак не характеризует фактическую эффективность контроля.

В терминах системного анализа этот факт становится очевидным. Оперативная характеристика представляет собой преобразователь, - вход, а 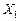, - два выхода (рис. 3.1.1).

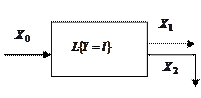
Рис. 3.1.1. Структурная схема системы выборочного контроля

Для однозначного определения выходных «сигналов» помимо характеристики преобразователя, очевидно, необходимо задание входного сигнала. Естественной вероятностной схемой в данной ситуации будет рассмотренная в п.1.3 формула вероятностей правдоподобия гипотез:

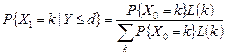, (3.1.3)

. (3.1.4)

Величины в знаменателе (3.1.3), (3.1.4), представляющие собой вероятности приемки и браковки 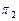соответственно, связаны очевидным соотношением .

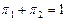2. Для уяснения «механизма» функционирования системы выборочного контроля рассмотрим модельный пример. Пусть из партии объема отбирается для контроля единиц. Решение о приемке принимается по «чистой» выборке 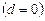. Оперативная характеристика такого плана будет иметь вид .

Пусть число дефектных единиц в предъявленной партии может принимать значения и имеет ряд распределения согласно табл. 3.1.1.

Таблица 3.1.1. Ряд распределения числа дефектных

единиц в предъявленной партии

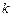
	0,40	0,30	0,20	0,07	0,02	0,01

Результаты вычислений по формулам (3.1.3), (3.1.4), (3.1.5) све-дены в табл. 3.1.2.

Таблица 3.1.2. Оперативная характеристика и распределение числа

дефектных единиц в предъявленных и проконтролированных партиях

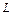
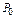
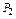
		0,400	0,444
	0,900	0,300	0,299	0,305
	0,809	0,200	0,179	0,388
	0,727	0,070	0,056	0,194
	0,652	0,020	0,014	0,071
	0,584	0,010	0,006	0,042

Как видно из табл. 3.1.2, в результате выборочного контроля происходит частичная сепарация предъявляемых партий. Ряд распределения смещается влево по оси 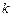(к нулю), а ряд , соответственно, вправо. Величины средней дефектности составят: , , . Вероятности приемки 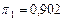и браковки 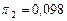численно равны удельной доле принятой и забракованной продукции в объеме поставки (при данном плане контроля и неизменном качестве поставок).

Условимся, что партии с не более чем двумя дефектными единицами являются приемлемыми . Тогда и являются оценками рисков потребителя в случае приемки без контроля и при наличии контроля (полный апостериорный риск потребителя). При такой же системе подсчета удельная доля годных партий среди забракованных (риск поставщика) оказывается непомерно велика: .

Однако если принять «справедливую» оценку – удельную долю напрасно забракованной продукции в объеме всей поставки (полный апостериорный риск поставщика), то результат выглядит вполне приемлемым: .

3. В рассмотренном примере был принят «нуль - дефектный» план контроля 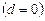. Главным недостатком такого плана является пологая оперативная характеристика. Однако при требовании нуль – дефектности поставок все многообразие планов естественным образом ограничивается планом с нулевым приемочным числом. Планы с и имеют более крутую оперативную характеристику. Оперативные характеристики и , рассчитанные по (3.1.2), показаны на рис. 3.1.2.

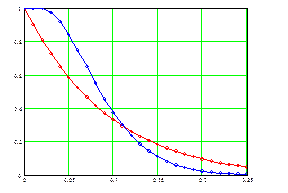
Рис. 3.1.2. Оперативные характеристики нуль – дефектного

плана (1) и плана с (2)

Собственное «качество» контрольного плана определяется крутизной наклонного участка оперативной характеристики. Идеальная оперативная характеристика, имеющая вид ступенчатой функции (1 при 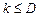и 0 при 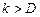), достигается только при сплошном контроле .

Соотношение (3.1.2) не очень удобно для практических расчетов, поэтому при больших 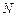и 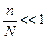целесообразно пользоваться биномиальной асимптотикой гипергеометрического распределения (п.1.1):

, (3.1.6)

где 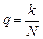. В свою очередь, при условии 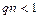биномиальный закон имеет пуассоновскую асимптотику:

, (3.1.7)

где .

При этом соотношения (3.1.3), (3.1.4) остаются справедливыми при любом виде оперативной характеристики.

4. Более гибкими с точки зрения «настройки» оперативной характеристики по сравнению с планами одинарной выборки являются ступенчатые планы. Рассмотрим план двойной выборки, заключающийся в следующем:

1) Из партии извлекается выборка объема (первая ступень).

2) Устанавливается приемочное число 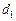и браковочное , то есть если число дефектных единиц в первой выборке партия принимается, если 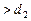- бракуется.

3) Если число дефектных единиц имеет промежуточное значение 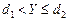, то извлекается вторая выборка объема .

4) Если суммарное число дефектных единиц не превосходит d ₂, партия принимается. В противном случае - бракуется.

Вторая ступень, очевидно, представляет собой план с оперативной характеристикой 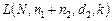, которая «включается» в случае браковки первой ступенью: . Вероятность включения второй ступени составляет .

Таким образом, согласно формуле полной вероятности (п.1.2) оперативная характеристика двухступенчатого плана будет иметь вид

. (3.1.8)

Преимущества характеристики (3.1.8), по сравнению с и , заключаются в том, что она более приближается к идеальной. Данную схему рассуждений можно обобщить на произвольное число ступеней. В результате приходим к рекуррентному соотношению:

, (3.1.9)

где 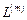- оперативная характеристика 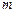- ступенчатого плана, - характеристика плана одинарной выборки объема с приемочным числом . За счет увеличения числа ступеней можно при меньшем среднем объеме контроля все более приближать браковочный уровень дефектности к средней дефектности поставок либо при прочих равных условиях уменьшать априорные риски потребителя и поставщика, определяемые по оперативной характеристике.

Вычисление оперативной характеристики по рекуррентной формуле (3.1.9) представляет известные неудобства. Однако существует более простой способ приближенного задания плана с неограниченно большим числом ступеней, так называемого плана последовательного контроля [7,10].

Дата добавления: 2014-12-26