Потоки случайных событий и их свойства

1. Основным исходным понятием теории надежности является отказ – нарушение работоспособности объекта, в результате чего объект перестает функционировать в заданном режиме, и становится невозможным его дальнейшее использование по назначению.

Отказы подразделяются на две принципиально различные группы:

– постепенные или параметрические – причинно обусловленные износом или старением составных частей изделия.

– внезапные – не имеющие видимой причинно-следственной связи, т.е. вызванные случайным сочетанием неблагоприятных факторов.

Объектом исследования математической теории надежности являются отказы второго типа, и поскольку в данной ситуации отказ интерпретируется как случайное событие, основанием математической теории надежности служит аппарат теории вероятностей и математической статистики.

С понятием отказ неразрывно связано второе исходное понятие – наработка до отказа – время, исчисляемое от начала функционирования до момента отказа. Причем, наряду с собственно временем, величина наработки может иметь и иную физическую природу (пробег, количество циклов срабатывания и т.д.).

При такой трактовке отказа и интерпретации объекта как невосстанавливаемого, наработка до отказа представляет собой положительно определенную СВ. Пусть f_T (t) – ПР наработки до отказа Т. Ее ФР имеет вероятностный смысл: 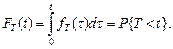Функция надежности (ВБР) определяется как дополнение 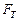до 1, т.е.

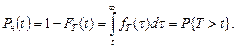(4.1.1)

Классификация технических объектов на невосстанавливаемые и восстанавливаемые определяется не собственно физической природой объекта, а, главным образом, выбранной в соответствии с целью исследования вероятностной схемой его функционирования. Например, осветительная лампа в светильнике или элемент в цепи электрического агрегата по своей природе являются одноразовыми, т.е. невосстанавливаемыми. Однако сам агрегат путем замены отказавшего элемента восстанавливает свою работоспособность. Показатели его надежности, очевидно, будут определяться законом распределения временного интервала между последовательными отказами. Если поиск и замена отказавшего элемента осуществляются не мгновенно, а также занимают некоторый временной интервал (детерминированный или случайный), то вероятностная схема должна быть соответствующим образом изменена. Но при любых возможных вариациях очевидно, что исходной, базовой вероятностной моделью служит поток однородных случайных событий. Поток случайных событий, или просто случайный поток, образуемый последовательностью однородных событий, происходящих в случайные моменты времени является принципиально отличным от ранее рассмотренных систем СВ. Наглядными примерами случайных потоков могут служить поток автомобилей на шоссе, поток вызовов на телефонной станции, заявок на станцию технического обслуживания, поток сбоев в работе компьютера, технологической линии и т.д. Смысл термина случайное событие применительно к потоку заключается не в том, какова вероятность его осуществления, а в том, сколько событий произойдет в течение временного интервала фиксированной длительности или через какое время произойдет очередное событие потока. Наиболее изученным и, в то же время, наиболее интересным с точки зрения практической применимости теоретических выводов являются ординарные потоки. Свойство ординарности заключается в том, что события происходят по одиночке (а не группами) или, строго говоря, вероятность одновременного появления двух и более событий пренебрежимо мала. При таких условиях единственным системообразующим элементом потока является интервал между соседними событиями 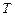, представляющий собой положительно-определенную СВ. Время, исчисляемое от начала отсчета до наступления 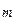-го события, представляет собой сумму

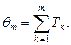
Наибольший интерес и практическую значимость представляет ситуация, когда все интервалы Т ₁, Т ₂… являются независимыми в совокупности СВ с одним законом распределения. Такой поток называется рекуррентным или потоком Пальма. Сам термин время не следует воспринимать буквально. Под ним может подразумеваться величина иной физической природы: расстояние (пробег), тонно-километры, киловатт-часы и т.д. Время может и не иметь размерности, и быть дискретным: количество циклов срабатывания, объем последовательной выборки, в частности, число испытаний по схеме Бернулли.

2. В качестве модельного примера рассмотрим поток «счастливых билетов». Каждый трамвайный билет имеет шестизначный десятичный номер, и «счастливым» принято считать билет, у которого сумма трех первых цифр равна сумме трех последних. Покупка очередного билета увеличивает дискретное «время» на 1, при этом, результат очередного испытания не зависит от предыдущих (другая смена, другой маршрут и т.д.) и определяется постоянной (стационарной) вероятностью 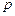. Таким образом, поток является рекуррентным, и после покупки счастливого билета отсчет начинается заново.

Вероятность р найдем по классической комбинаторной схеме. Общее число различимых номеров составляет N =10⁶ (000 000÷999 999). Для определения числа счастливых комбинаций рассмотрим S ⁽ⁿ⁾ – сумму n случайных десятичных цифр. Для n =1 ряд распределения очевиден:

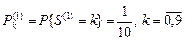. (4.1.2)

Для n >1 по теореме о свертке (п.1.3) будет справедливо рекуррентное соотношение:

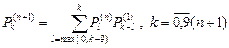. (4.1.3)

Для рассматриваемой задачи достаточно найти ряд 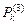, k= 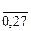, приведенный в табл.4.1.1 для одного из симметричных отрезков{0÷13}; {14÷27}.

Каждая комбинация первых трех цифр, удовлетворяющая условию S ⁽³⁾= k, может сочетаться с любой из комбинаций трех вторых, удовлетворяющей тому же условию. Следовательно, искомое число счастливых комбинаций равно скалярному квадрату строки 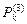из табл. 4.1.1: 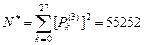,и искомая вероятность составит 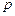=55252×10^-6»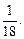

Таблица 4.1.1. Ряд распределения суммы 3 случайных десятичных цифр

k

…

…

…

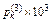
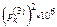
Интервал между последовательными событиями Т будет иметь геометрическое распределение 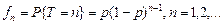Для вычисления числовых характеристик Т введем производящую функцию:

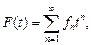(4.1.4)

где 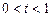– веще ственная переменная. Дважды дифференцируя (4.1.4), получим:

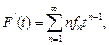
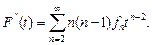(4.1.5)

Подставляя в (4.1.5) 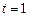, замечаем, что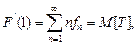

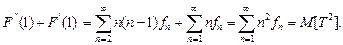
Таким образом, получаем соотношения:

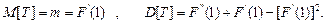(4.1.6)

Раскрывая ряд (4.1.4), производящую функцию 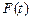получим в виде

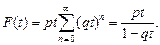(4.1.7)

Подставляя (4.1.7) в (4.1.6), находим числовые характеристики:

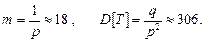(4.1.8)

На основании (4.1.8) перепишем ряд распределения в виде

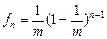(4.1.9)

и условимся, что каждое испытание занимает время 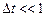, так что .

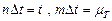Тогда для (4.1.9) будет справедлива асимптотика:

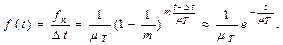(4.1.10)

Выражение (4.1.10) представляет собой ПР показательного закона

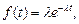(4.1.11)

где 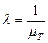- параметр распределения.

Величину 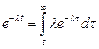можно истолковать как вероятность того, что за время t не произойдет ни одного события. Соответственно, 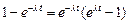- есть вероятность наступления хотя бы одного события. Разлагая в последнем выражении 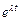в ряд Маклорена, получаем полную группу по числу событий:

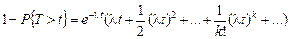. (4.1.12)

Объединяя (4.1.11) и (4.1.12), приходим к выводу, что число событий в потоке за интервал t имеет пуассоновское распределение с параметром :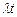

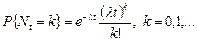(4.1.13)

Пусть Т ^(k) - время реализаций k событий, тогда

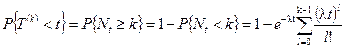(4.1.14)

Дифференцируя (4.1.14) по t, найдем ПР Т ^(k):

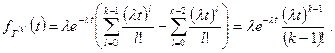(4.1.15)

Полученная ПР представляет собой закон Эрланга k -го порядка (k -кратная автосвертка показательного закона).

3. Возвращаясь к простейшему показательному потоку, остановимся на условиях его возникновения. В большинстве практически значимых ситуаций модель исследуемого потока представима в виде суммы (суперпозиции) нескольких парциальных потоков. Так, например, рассмотренный поток счастливых билетов, представляет собой суперпозицию 28 элементарных парциальных потоков по числу возможных значений суммы 3 десятичных цифр. Сущность сложения потоков очевидна из рис. 4.1.2.

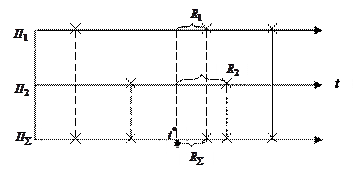
Рис. 4.1.2. Сложение случайных потоков

Суммарный поток складывается из событий всех парциальных потоков, так что время ожидания в суммарном потоке определяется как

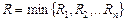. (4.1.16)

Закон распределения минимума в пределе при n ®¥ имеет показательный вид. Стало быть, такую же показательную ПР имеет интервал между соседними событиями потока. Чтобы среднее значение интервала 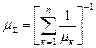не стремилось к нулю при увеличении n, время в суммарном потоке можно отмасштабировать t '= nt, что эквивалентно прореживанию потока в соотношении 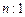. Тогда получим простейший поток с усредненной плотностью:

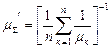. (4.1.17)

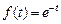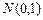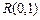Таким образом, показательный закон , наряду с и , является одним из трех важнейших законов (стационарных точек) в пространстве непрерывных распределений. Для случайных потоков с непрерывным временем показательный закон имеет такое же значение, какое нормальный закон имеет для сумм СВ.

Дата добавления: 2014-12-26