Статистическая оценка параметра показательного закона

1. Поскольку надежность проявляет себя только в процессе эксплуатации технического изделия, то единственным источником объективной информации о надежности являются испытания.

Под испытанием понимается сбор информации о функционировании объекта в процессе его реальной эксплуатации либо в процессе специально организованной процедуры, имитирующей условия эксплуатации.

В зависимости от цели исследования испытания подразделяются на 2 типа:

– определительные испытания – для установления закона функционирования изделий;

– контрольные испытания – для подтверждения соответствия по показателям надежности.

Отличительным признаком определенных испытаний является большой объем (репрезентативность) выборки однотипных изделий и испытания до последнего отказа, т.е. с большим числом полных реализаций (наработок до отказа).

Результаты контрольных испытаний представляют собой усеченные данные, и в процессе испытаний может быть не зарегистрировано ни одного отказа. Проблеме испытаний на надежность посвящено большое число специализированных руководств, где методика сбора и обработки результатов классифицируются в зависимости от цели исследования, характера исходной информации и т.д.

Далее рассмотрим методику вычисления точечных и интервальных оценок средней наработки до отказа при показательном законе функционирования.

Пусть на испытания поставлено N однотипных изделий, и в течение времени испытаний T _n было зарегистрировано n отказов с наработками t ₁, t ₂,..., t _n. С учетом независимости в совокупности отказов (и безотказных наработок) и, стало быть, применимости схемы Бернулли вероятность такой комбинации можно представить в виде

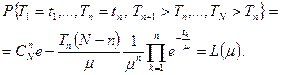(4.4.1)

Методика точечной оценки неизвестного параметра m была предложена Р. Фишером и носит название метод максимального правдоподобия Фишера. Методика заключается в следующем. В качестве точечной оценки (наиболее вероятного значения) неизвестного параметра m принимается точка максимума L (m) (4.4.1). Поскольку L (m) является положительно-определенной, ее точка максимума, очевидно, совпадает с точкой максимума ее логарифма. Приравнивая 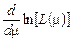к нулю, получим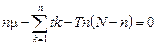

откуда находим

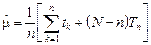. (4.4.2)

Интерпретация точечной оценки (4.4.2) имеет вполне очевидный «физический» смысл. Выражение в квадратных скобках представляет собой суммарную наработку N изделий (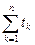 - сумма всех полных реализаций – наработок до отказа, (N-n) T _n - сумма всех неполных реализаций – безотказных наработок). Таким образом 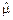по (4.4.2) представляет собой отношение полной суммарной наработки к числу отказов, зарегистрированных в течение времени испытаний T _n.

2. Для прогнозирования результата единичного опыта более адекватны доверительные интервальные оценки вида

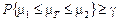, (4.4.3)

где g - доверительная вероятность (вероятность покрытия интервалом 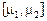) неизвестного значения m_T. Показательный закон с ПР 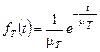преобразованием 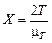приводится к виду

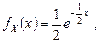(4.4.4)

который, как было показано в п.1.3, представляет собой сумму квадратов двух независимых стандартных нормальных СВ, т.е. 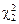. На основании аддитивности распределения 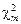по степеням свободы (т.е. 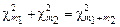). Для суммарной наработки T _S будет справедливо соотношение 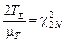, откуда получаем

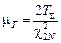. (4.4.5)

Таким образом, доверительный интервал будет определяться межквантильной g-широтой,

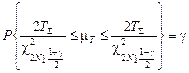. (4.4.6)

Глава 5. Статистическое моделирование

Дата добавления: 2014-12-26