
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выборке1
|
|
|
|
Алгоритмы Монте-Карло, экспериментальные и расчетные
значения инвариантов структуры серий в последовательной
А. Текст программы статистического моделирования, расчетное среднее значение и границы 90% доверительного интервала, а также усредненные по 20 реализациям экспериментальные значения длины максимальной «знаковой» серии (положений относительно медианы) в зависимости от объема последовательной выборки из 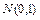 .
.
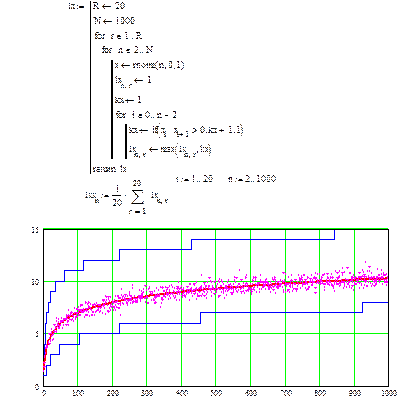
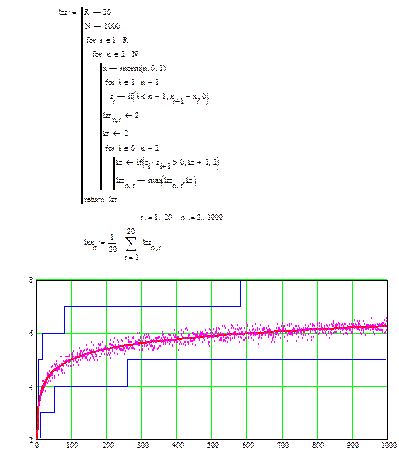
Б. Текст программы статистического моделирования, расчетное среднее значение, границы доверительного 90% интервала и усредненные по 20 реализациям экспериментальные значения длины максимальной «трендовой» серии в зависимости от объема последовательной выборки из 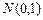 .
.
В. Расчетные средние значения, СКО и границы 90% доверительного интервала для длины максимальной «знаковой» (табл.1) и «трендовой» (табл.2) серий. В скобках скобках указаны границы 95% доверительного интервала.
Таблица 1
| Объем выборки, n | 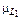
| 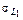
| НГ | ВГ |
| 1,50 | 0,50 | |||
| 2,00 | 0,71 | |||
| 2,38 | 0,86 | |||
| 2,69 | 0,98 | |||
| 2,94 | 1,09 | 2(1) | 5(6) | |
| 3,16 | 1,18 | 5(6) | ||
| 3,34 | 1,25 | |||
| 3,51 | 1,30 | 6(7) | ||
| 3,66 | 1,35 | 6(7) | ||
| 3,92 | 1,43 | |||
| 4,15 | 1,48 | 7(8) | ||
| 4,34 | 1,52 | 3(2) | 7(8) | |
| 4,51 | 1,55 | 3(2) | 7(8) | |
| 4,66 | 1,58 | |||
| 4,98 | 1,63 | 8(9) | ||
| 5,24 | 1,66 | 8(9) | ||
| 5,66 | 1,70 | 4(3) | 9(10) | |
| 5,98 | 1,73 | 9(10) | ||
| 6,98 | 1,79 | 5(4) | 10(11) | |
| 7,98 | 1,83 | 6(5) | 11(12) | |
| 8,56 | 1,84 | 12(13) | ||
| 9,30 | 1,85 | 13(14) | ||
| 9,78 | 1,86 | 13(14) | ||
| 10,30 | 1,86 | 14(15) |
Таблица 2
| Объем выборки, n | 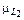
| 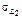
| НГ | ВГ |
| 2,00 | 0,00 | |||
| 2,33 | 0,47 | |||
| 2,67 | 0,62 | |||
| 2,90 | 0,68 | |||
| 3,08 | 0,70 | 4(5) | ||
| 3,22 | 0,71 | 4(5) | ||
| 3,33 | 0,71 | |||
| 3,42 | 0,72 | 3(2) | ||
| 3,50 | 0,73 | 3(2) | ||
| 3,63 | 0,75 | |||
| 3,74 | 0,76 | |||
| 3,83 | 0,77 | |||
| 3,92 | 0,78 | 5(6) | ||
| 3,99 | 0,78 | 5(6) | ||
| 4,14 | 0,77 | 5(6) | ||
| 4,27 | 0,77 | |||
| 4,45 | 0,76 | |||
| 4,58 | 0,76 | |||
| 4,99 | 0,76 | 6(7) | ||
| 5,39 | 0,73 | |||
| 5,61 | 0,72 | |||
| 5,88 | 0,73 | |||
| 6,06 | 0,71 | 7(8) | ||
| 6,25 | 0,69 | 7(8) |
Г. Генерирующая программа, гистограмма 200 реализаций, сглаживающие теоретические функции Гаусса и числовые характеристики спектра знаковых серий.
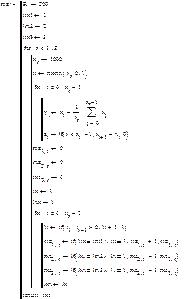
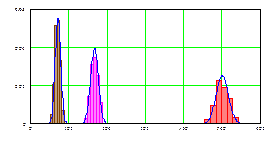
Среднее значение и дисперсия числа знаковых серий в зависимости
от длины серии 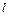
| l | 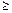 7 7
| ||||||
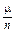
| 0,5 | 0,167 | 0,071 | 0,033 | 0,016 | 0,008 | 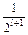
|
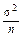
| 0,25 | 0,102 | 0,052 | 0,027 | 0,014 | 0,007 | 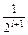
|
Д. Генерирующая программа, гистограмма 200 реализаций, сглаживающие теоретические функции Гаусса и числовые характеристики спектра трендовых серий.
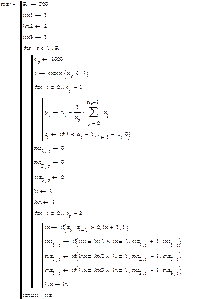
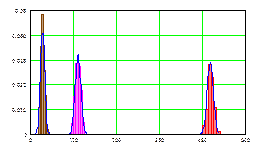
Средние и дисперсии числа трендовых серий в зависимости
от длины серии
| l | 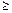 6 6
| ||||
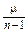
| 0,5 | 0,132 | 0,034 | 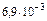
| 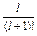
|
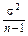
| 0,074 | 0,060 | 0,026 | 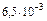
| 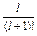
|
Приложение II
Таблица распределения Кохрэна
Значения 95% квантилей статистики Кохрэна для оценки дисперсионной однородности совокупности и ее подгрупп (n – объем подгрупп, к – число подгрупп)
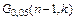
| к \ n -1 | |||||||
| 0,9985 | 0,9750 | 0,9392 | 0,9057 | 0,8772 | 0,8534 | 0,8332 | |
| 0,9669 | 0,8709 | 0,7977 | 0,7457 | 0,7071 | 0,6771 | 0,6530 | |
| 0,9065 | 0,7679 | 0,6841 | 0,6287 | 0,5895 | 0,5598 | 0,5365 | |
| 0,8412 | 0,6838 | 0,5981 | 0,5440 | 0,5063 | 0,4783 | 0,4564 | |
| 0,7808 | 0,6161 | 0,5321 | 0,4803 | 0,4447 | 0,4184 | 0,3980 | |
| 0,7271 | 0,5612 | 0,4800 | 0,4307 | 0,3974 | 0,3726 | 0,3535 | |
| 0,6798 | 0,5175 | 0,4377 | 0,3910 | 0,3595 | 0,3362 | 0,3185 | |
| 0,6385 | 0,4775 | 0,4027 | 0,3584 | 0,3286 | 0,3067 | 0,2901 | |
| 0,6020 | 0,4450 | 0,3733 | 0,3311 | 0,3029 | 0,2823 | 0,2666 | |
| 0,5410 | 0,3924 | 0,3264 | 0,2880 | 0,2624 | 0,2439 | 0,2299 | |
| 0,4709 | 0,3346 | 0,2758 | 0,2419 | 0,2195 | 0,2034 | 0,1911 | |
| 0,3894 | 0,2705 | 0,2205 | 0,1921 | 0,1735 | 0,1602 | 0,1501 | |
| 0,3434 | 0,2354 | 0,1907 | 0,1656 | 0,1493 | 0,1374 | 0,1286 | |
| 0,2929 | 0,1980 | 0,1593 | 0,1377 | 0,1237 | 0,1137 | 0,1061 | |
| 0,2370 | 0,1576 | 0,1259 | 0,1082 | 0,0968 | 0,0887 | 0,0827 | |
| 0,1737 | 0,1131 | 0,0895 | 0,0765 | 0,0682 | 0,0623 | 0,0583 | |
| 0,0998 | 0,0632 | 0,0495 | 0,0419 | 0,0371 | 0,0337 | 0,0312 |
Окончание прил. II
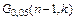
| к \ n -1 | 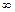
| ||||||
| 0,8159 | 0,8010 | 0,7880 | 0,7341 | 0,6602 | 0,5813 | 0,5000 | |
| 0,6333 | 0,6167 | 0,6025 | 0,5466 | 0,4748 | 0,4031 | 0,3333 | |
| 0,5175 | 0,5017 | 0,4884 | 0,4366 | 0,3720 | 0,3093 | 0,2500 | |
| 0,4387 | 0,4241 | 0,4118 | 0,3645 | 0,3066 | 0,2513 | 0,2000 | |
| 0,3817 | 0,3682 | 0,3568 | 0,3135 | 0,2612 | 0,2119 | 0,1667 | |
| 0,3384 | 0,3259 | 0,3154 | 0,2756 | 0,2278 | 0,1833 | 0,1429 | |
| 0,3043 | 0,2926 | 0,2829 | 0,2462 | 0,2022 | 0,1616 | 0,1250 | |
| 0,2768 | 0,2659 | 0,2568 | 0,2226 | 0,1820 | 0,1446 | 0,1111 | |
| 0,2541 | 0,2439 | 0,2353 | 0,2032 | 0,1655 | 0,1308 | 0,1000 | |
| 0,2187 | 0,2098 | 0,2020 | 0,1737 | 0,1403 | 0,1100 | 0,0833 | |
| 0,1815 | 0,1736 | 0,1671 | 0,1429 | 0,1144 | 0,0889 | 0,0667 | |
| 0,1422 | 0,1357 | 0,1303 | 0,1108 | 0,0879 | 0,0675 | 0,0500 | |
| 0,1216 | 0,1160 | 0,1113 | 0,0942 | 0,0743 | 0,0567 | 0,00417 | |
| 0,1002 | 0,0958 | 0,0921 | 0,0771 | 0,0604 | 0,0457 | 0,0333 | |
| 0,0780 | 0,0745 | 0,0713 | 0,0595 | 0,0462 | 0,0347 | 0,0250 | |
| 0,0552 | 0,0520 | 0,0497 | 0,0411 | 0,0316 | 0,0234 | 0,0167 | |
| 0,0292 | 0,0279 | 0,0266 | 0,0218 | 0,0165 | 0,0120 | 0,0083 |
Приложение III
Таблица распределения выбороного размаха
Значения 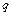 -% квантилей выборочного размаха
-% квантилей выборочного размаха 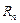 , отнесенного к параметру
, отнесенного к параметру 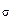 исходного распределения; математическое ожидание
исходного распределения; математическое ожидание 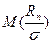 и среднее квадратическое отклонение
и среднее квадратическое отклонение 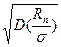 этого же отношения в долях параметра
этого же отношения в долях параметра 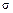 исходного распределения
исходного распределения
| n | 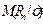
| 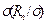
| 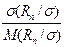
| Вероятность 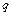 в процентах в процентах
| ||||||||
| 0,05 | 0,1 | 0,5 | 1,0 | 2,5 | 5,0 | 10,0 | 20,0 | 30,0 | ||||
| 1,128 | 0,853 | 0,756 | 0,00 | 0,00 | 0,01 | 0,02 | 0,04 | 0,09 | 0,18 | 0,36 | 0,55 | |
| 1,693 | 0,888 | 0,525 | 0,04 | 0,06 | 0,13 | 0,19 | 0,30 | 0,43 | 0,62 | 0,90 | 1,14 | |
| 2,059 | 0,880 | 0,427 | 0,16 | 0,20 | 0,34 | 0,43 | 0,59 | 0,76 | 0,98 | 1,29 | 1,53 | |
| 2,326 | 0,864 | 0,371 | 0,31 | 0,37 | 0,55 | 0,66 | 0,85 | 1,03 | 1,26 | 1,57 | 1,82 | |
| 2,534 | 0,848 | 0,335 | 0,47 | 0,54 | 0,75 | 0,87 | 1,06 | 1,25 | 1,49 | 1,80 | 2,04 | |
| 2,704 | 0,833 | 0,308 | 0,61 | 0,69 | 0,92 | 1,05 | 1,25 | 1,44 | 1,68 | 1,99 | 2,22 | |
| 2,847 | 0,820 | 0,288 | 0,75 | 0,83 | 1,08 | 1,20 | 1,41 | 1,60 | 1,83 | 2,14 | 2,38 | |
| 2,970 | 0,808 | 0,272 | 0,88 | 0,96 | 1,21 | 1,34 | 1,55 | 1,74 | 1,97 | 2,28 | 2,51 | |
| 3,078 | 0,797 | 0,259 | 1,00 | 1,08 | 1,33 | 1,47 | 1,67 | 1,86 | 2,09 | 2,39 | 2,62 | |
| 3,173 | 0,787 | 0,248 | 1,10 | 1,20 | 1,45 | 1,58 | 1,78 | 1,97 | 2,20 | 2,50 | 2,72 | |
| 3,258 | 0,778 | 0,239 | 1,21 | 1.30 | 1,55 | 1,68 | 1,88 | 2,07 | 2,30 | 2,59 | 2,82 | |
| 3,336 | 0,770 | 0,231 | 1,30 | 1,39 | 1,64 | 1,77 | 1,97 | 2,16 | 2,39 | 2,68 | 2,90 | |
| 3,407 | 0,762 | 0,224 | 1,38 | 1,48 | 1,72 | 1,86 | 2,06 | 2,24 | 2,47 | 2,75 | 2,97 | |
| 3,472 | 0,755 | 0,217 | 1,46 | 1,56 | 1,80 | 1,93 | 2,14 | 2,32 | 2,54 | 2,83 | 3,04 | |
| 3,532 | 0,749 | 0,212 | 1,53 | 1,63 | 1,88 | 2,01 | 2,21 | 2,39 | 2,61 | 2,89 | 3,11 | |
| 3,588 | 0,743 | 0,207 | 1,60 | 1,69 | 1,94 | 2,07 | 2,27 | 2,45 | 2,67 | 2,95 | 3,17 | |
| 3,640 | 0,738 | 0,20 | 1,66 | 1,75 | 2,01 | 2,14 | 2,34 | 2,51 | 2,73 | 3,01 | 3,22 | |
| 3,689 | 0,733 | 0,199 | 1,72 | 1,82 | 2,07 | 2,20 | 2,39 | 2,57 | 2,79 | 3,06 | 3,27 | |
| 3,735 | 0,729 | 0,195 | 1,78 | 1,88 | 2,12 | 2,25 | 2,45 | 2,63 | 2,84 | 3,11 | 3,32 |
Окончание прил. III
| n | Вероятность в процентах | |||||||||||
| 40,0 | 50,0 | 60,0 | 70,0 | 80,0 | 90,0 | 95,0 | 97,5 | 99,0 | 99,5 | 99,9 | 99,95 | |
| 0,74 | 0,95 | 1,20 | 1,47 | 1,81 | 2,33 | 2,77 | 3,17 | 3,64 | 3,97 | 4,65 | 4,92 | |
| 1,36 | 1,59 | 1,83 | 2,09 | 2,42 | 2,90 | 3,31 | 3,68 | 4,12 | 4,42 | 5,06 | 5,31 | |
| 1,76 | 1,98 | 2,21 | 2,47 | 2,78 | 3,24 | 3,63 | 3,98 | 4,40 | 4,69 | 5,31 | 5,56 | |
| 2,04 | 2,26 | 2,48 | 2,73 | 3,04 | 3,48 | 3,86 | 4,20 | 4,60 | 4,89 | 5,48 | 5,72 | |
| 2,26 | 2,47 | 2,69 | 2,94 | 3,23 | 3,66 | 4,03 | 4,36 | 4,76 | 5,03 | 5,62 | 5,86 | |
| 2,44 | 2,65 | 2,86 | 3,10 | 3,39 | 3,81 | 4,17 | 4,49 | 4,88 | 5,15 | 5,73 | 5,96 | |
| 2,59 | 2,79 | 3,00 | 3,24 | 3,52 | 3,93 | 4,29 | 4,61 | 4,99 | 5,26 | 5,82 | 6,04 | |
| 2,71 | 2,92 | 3,12 | 3,35 | 3,63 | 4,04 | 4,39 | 4,70 | 5,08 | 5,34 | 5,90 | 6,12 | |
| 2,83 | 3,02 | 3,23 | 3,46 | 3,73 | 4,13 | 4,47 | 4,79 | 5,16 | 5,42 | 5,97 | 6,19 | |
| 2,93 | 3,12 | 3,32 | 3,55 | 3,82 | 4,21 | 4,55 | 4,86 | 5,23 | 5,49 | 6,04 | 6,25 | |
| 3,01 | 3,21 | 3,41 | 3,63 | 3,90 | 4,29 | 4,62 | 4,92 | 5,29 | 5,54 | 6,09 | 6,31 | |
| 3,09 | 3,29 | 3,48 | 3,70 | 3,97 | 4,35 | 4,69 | 4,99 | 5,35 | 5,60 | 6,14 | 6,36 | |
| 3,17 | 3,36 | 3,55 | 3,77 | 4,03 | 4,41 | 4,74 | 5,04 | 5,40 | 5,65 | 6,19 | 6,40 | |
| 3,23 | 3,42 | 3,62 | 3,83 | 4,09 | 4,47 | 4,80 | 5,09 | 5,45 | 5,70 | 6,23 | 6,45 | |
| 3,30 | 3,48 | 3,67 | 3,89 | 4,14 | 4,52 | 4,85 | 5,14 | 5,49 | 5,74 | 6,28 | 6,49 | |
| 3,35 | 3,54 | 3,73 | 3,94 | 4,19 | 4,57 | 4,89 | 5,18 | 5,54 | 5,79 | 6,32 | 6,52 | |
| 3,41 | 3,59 | 3,78 | 3,99 | 4,24 | 4,61 | 4,93 | 5,22 | 5,57 | 5,82 | 6,35 | 6,56 | |
| 3,46 | 3,64 | 3,83 | 4,03 | 4,29 | 4,65 | 4,97 | 5,26 | 5,61 | 5,86 | 6,38 | 6,59 | |
| 3.51 | 3,69 | 3,87 | 4,08 | 4,33 | 4,69 | 5,01 | 5,30 | 5,65 | 5,89 | 6,41 | 6,62 |
Учебное издание
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 381; Нарушение авторских прав?; Мы поможем в написании вашей работы!