Выборочные оценки числовых индексов воспроизводимости

1. В литературе и нормативных документах, посвященных статистическому контролю производственных процессов, в недавнее время широкое распространение получила методика оценки значимости технологического рассеяния и правильности настройки посредством так называемых индексов воспроизводимост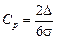и:

и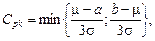

где D- полуширина поля допуска; s- СКО технологического рассеяния; m - фактический номинал настройки процесса; а и b - соответственно нижняя и верхняя границы поля допуска.

Вероятностный и «физический» смысл величин 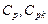при таком определении вполне прозрачен и не вызывает никакой двусмысленности. Однако на практике числовые характеристики m и s, как правило, неизвестны и заменяются выборочными оценками 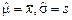(п.1.4). При этом объем выборки обычно невелик и составляет порядка 50 значений. В данной ситуации 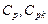превращаются в выборочные статистики, а стало быть СВ, и для того чтобы оценка процесса посредством 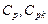была адекватной, необходимо установить их законы распределения. В качестве исходного соотношения рассмотрим ПР выборочного СКО стандартного нормального распределения (п.1.4):

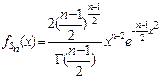. (5.3.1)

Пусть 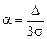- «точное» значение индекса 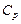(принято руководствоваться двумя контрольными нормативами: - удовлетворительная воспроизводимость, 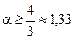– хорошая воспроизводимость). Выборочную оценку 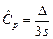преобразуем к виду 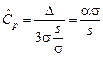. Таким образом, при любом значении s (от m С _р, в принципе, не зависит) ПР выборочной 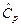идентична ПР СВ 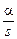, где s - выборочное СКО стандартной нормальной совокупности. Искомую ПР величины 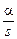найдем путем суперпозиции преобразований 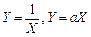(п.1.1):

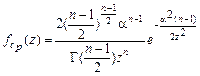. (5.3.2)

2. При выводе ПР выборочного 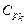будем полагать, что процесс настроен на центр поля допуска (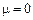). В этом случае точные значения 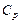и 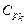будут совпадать: 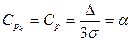. Из определения 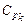очевидно, что его можно представить в виде

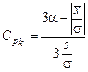. (5.3.3)

Таким образом, поскольку 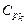не зависит от 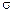, достаточно рассмотреть выборку из 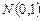. При этом ограничение 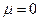также несущественно и при 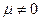сводится лишь к сдвигу по параметру .

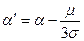Закон распределения выборочного 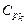найдем как ПР функции от 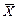и 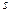. Сначала, согласно общей методике (п.1.3), найдем 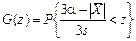. Для этого придется рассмотреть 2 случая: 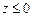и 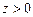(рис.5.3.1, 5.3.2).

Плотность совместного распределения СВ 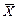и 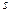, как следует из установленной в п.1.4 их независимости, равна произведению ПР компонент. Интегрируя ПР совместного распределения по области D (z), получаем

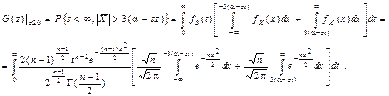(5.3.4)

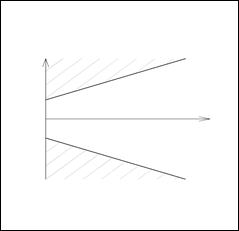
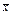
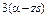
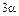
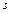
0

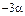
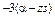
Рис. 5.3.1. Схема области интегрирования для определения

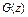в координатах 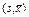при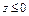

Дифференцируя (5.3.4) по 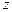, находим:

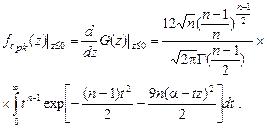(5.3.5)

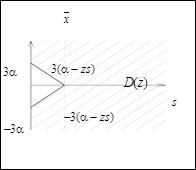Рис. 5.3.2. Схема области интегрирования для определения

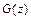в координатах 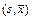при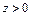

В этом случае 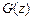будет иметь вид

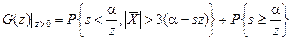. (5.3.6)

После дифференцирования по 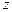получим

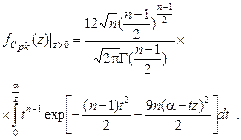(5.3.7)

3. Как видно из формул (5.3.5), (5.3.7), 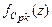имеет, вообще говоря, особенность в точке 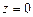. Однако эта особенность является устранимой (непрерывность в точке 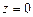не нарушается) и, поскольку левый «хвост» 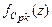при 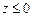ничтожно мал, не представляет практического интереса. Интерес представляет тот факт, что выборочные оценк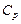и и 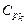имеют значительное положительное смещение, которое по непонятным причинам игнорируется как в литературе, так и в нормативных документах (стандартах, методических указаниях и т.д.), посвященных статистическому контролю производственных процессов. Имеющиеся в распоряжении ПР (5.3.5), (5.3.7) в принципе позволяют, вычислив средние значения статистик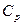и и 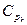, определить величину смещения и скомпенсировать его по аналогии с выборочными дисперсией и СКО (п.1.4) посредством поправочных коэффициентов. Однако даже с учетом этих уточнений придется признать, что общепринятая на сегодняшний день методика определения числовых индексов воспроизводимости сформулирована не совсем удачно. Более рациональным представляется перейти к обратным величинам:

.

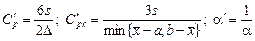Главным доводом в пользу этого является существенное повышение эффективности оценок (СКО «штрихованных» статистик примерно в 4 раза меньше, чем у исходных). Кроме того, устанавливается единообразие с другими числовыми показателями качества: с оценкой вероятности выхода несоответствующей единицы продукции, оценкой доли несоответствующих единиц продукции в партии, рисков поставщика и потребителя и т.д., где идеальному процессу соответствуют нулевые значения показателей. В предлагаемом варианте область значений удовлетворительного процесса составит 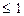, хорошего – 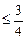вместо 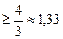. Их ПР легко вычисляются с помощью преобразования 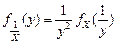(п.1.1), и возникающее отрицательное смещение можно без проблем компенсировать. Однако более предпочтительным с точки зрения практической применимости представляется определение для каждого нормативного значения одностороннего доверительного (90%-95%) интервала, выход за верхнюю границу которого естественно интерпретировать как разладку процесса. Сравнительный вид ПР величин 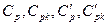приведен на рис.5.3.3.

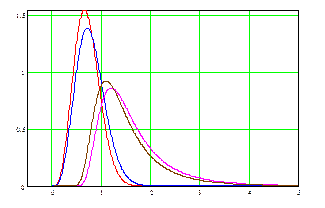
Рис. 5.3.3. Плотности распределения величин

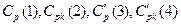при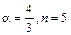

Список Литературы

1. Бернштейн, С.Н. Теория вероятностей. / C.Н. Бернштейн. — Изд. 4-е перераб. И доп. М.-Л.: ОГИЗ, 1946.

2. Вентцель, Е.С., Овчаров, Л.А. Теория вероятностей и ее инженерные приложения / Е.С. Вентцель, Л.А. Овчаров. — М.: Высш. шк., 2000.

3. Вентцель, Е.С., Овчаров, Л.А Теория случайных процессов и ее инженерные приложения / Е.С. Вентцель, Л.А. Овчаров. — М.: Высш. шк., 2003.

4. Крамер, Г. Математические методы статистики /

Г. Крамер. — М.: Мир, 1976.

5. Корн, Г., Корн, Т. Справочник по математике / Г. Корн, Т. Корн. — М.: Наука, 1984.

6. Макаров, В.В. Mathcad – 2001 учебный курс / В.В. Макаров.

— С.Пб.: Питер, 2004.

7.. Смирнов, Н.В., Барковский, И.В. Теория вероятностей и математическая статистика в технике (общая часть) / Н.В. Смирнов, И.В. Барковский. — М.; Наука, 1965.

8. Плотников, А.Н. Закон распределения длины максимальной серии и его статистические приложения / А.Н. Плотников // Известия СНЦ РАН, 2006. Т. 8, №4- С.1047-1056.

9. Плотников, А.Н. Об инвариантах структуры серий и критериях случайности последовательной выборки./ А.Н. Плотников // Известия СНЦ РАН, 2006. Т.8, №4.- С.1142-1147.

10. Феллер, В. Введение в теорию вероятностей и ее приложения Т.1 / В. Феллер. — М.: Мир, 1983.

11. Финни, Д. Введение в теорию планирования эксперимента / Д. Финни. — М.: Наука, 1970.

12. Хикс, Ч. Основные принципы планирования эксперимента / Ч. Хикс. — М.: Мир, 1997.

Приложение I

Дата добавления: 2014-12-26