Параметрический способ представления результатов исследования

90 66 106 84 105 83 104 82 97 97 59 95 78 70 47 95 100 69 44 80 75 75 51 109 89 58 59 72 74 75 81 71 68 112 62 91 93 84

Пример.

Ученикам начальной школы (38 человек) был предложен тест для проверки скорости чтения. Были получены следующие оценки скорости чтения (количество слов за минуту):

Результаты расчетов:

R= x_max – x_min = 112 – 44 = 68

Пусть k = 8 Тогда 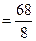= 8,5 ≈ 9

Пусть начало первого интервала будет x₀₁=41.

Тогда верхняя граница первого интервала будет x₁=41+(9-1)=49

Начало второго интервала на 1 балл больше, то есть x₀₂=50.

Верхняя граница второго интервала x₂=50+(9-1)=58. И так далее…

Таблица 5

№ п/п	Xi (начало и конец интервалов)	fi	Fi
	104—112
	95—103
	86—94
	77—85
	68—76
	59—67
	50—58
	41—49
		S=38

Построим на основании этого примера графики — полигоны частот и гистограммы дифференциального и интегрального распределений (рис. 6-9).

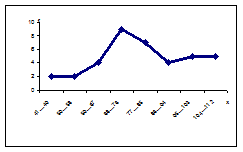Рис. 6. Полигон частот дифференциального распределения	Рис. 7. Гистограмма дифференциального распределения
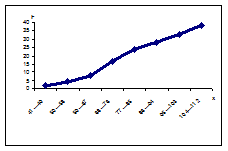Рис.8. Полигон частот интегрального распределения	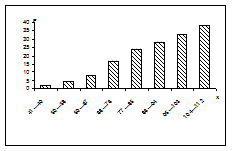Рис. 9. Гистограмма интегрального распределения

— это описание результатов, полученных на выборке с помощью параметров распределений.

Параметры распределений — это числовые характеристики, которые отражают основные тенденции выраженности и изменчивости признака в данной выборке.

Существуют две группы параметров: меры положения или меры центральной тенденции, отражающие выраженность признака, и меры изменчивости или меры рассеивания, характеризующие изменчивость признака. Выбор параметров, с помощью которых будут описываться результаты исследования, зависит, во-первых, от того, по какой шкале измерен данный признак, и, во-вторых, от исследовательских задач.

Для облегчения принятия решения о выборе параметров следует воспользоваться таблицей 6.

Таблица 6

Дата добавления: 2014-12-26