Проверка на выскакивание наибольшего значения

Исключение выскакивающих значений

Рассмотрим пример расчета параметров для сгруппированного распределения.

Таблица 9

№ п/п	Xi (начало и конец интервалов)	fi	Fi	Xср i
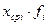
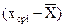
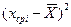
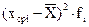
	104—112				108×5=540	108–80,5=27,5	27,5^2=756,25	756,25×5=3781,25
	95—103				99×5=495	99–80,5=18,5	18,5^2=342,25	342,25×5=1711,25
	86—94				90×4=360	90-80,5=9,5	9,5^2=90,25	90,25×4=361,00
	77—85				81×7=567	81–80,5=0,5	0,5^2=0,25	0,25×7=1,75
	68—76				72×9=648	72–80,5= –8,5	(–8,5)^2=72,25	72,25×9=650,25
	59—67				63×4=252	63–80,5= –17,5	(–17,5)^2=306,25	306,25×4=1225,00
	50—58				54×2=108	54–80,5= –26,5	(–26,5)^2=702,25	702,25×2=1404,50
	41—49				45×2=90	45–80,5= –35,5	(–35,5)^2=1260,25	1260,25×2=2520,50
		S=38			S=3060			S=11655,50

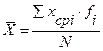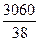= =80,5

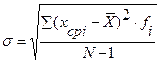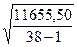= =17,7

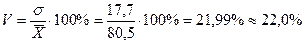
Выскакивающими называются крайние значения (максимальные или минимальные), далеко отстоящие от ближайших к ним значений.

Способ проверки крайних значений «на выскакивание» основан на оценке соотношения «расстояния» крайних значений (вариант) и ближайших к ним и размаха всех значений.

Данный способ проверки описан в книге: Ашмарин И. В., Воробьев А. А. Статистические методы в микробиологических исследованиях. — Л., 1962.

А) Когда одно наибольшее значение подозревается в выскакивании

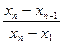
где x_n — наибольшее значение, которое подозревается в выскакивании;

x_n-1 — значение, следующее за наибольшим в сторону убывания;

x₁ — наименьшее значение.

Б) Когда есть основания полагать, что и наименьшее значение является выскакивающим; но проверяется все же одно наибольшее значение.

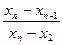
где x_n — наибольшее значение, которое подозревается в выскакивании;

x_n-1 — значение, следующее за наибольшим в сторону убывания;

x₂ — наименьшее значение.

В) Когда предполагается, что выскакивающими являются сразу два наибольших значения

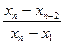
где x_n — наибольшее значение, которое подозревается в выскакивании;

x_n-2 — значение, следующее за двумя наибольшими в сторону убывания;

x₁ — наименьшее значение.

Дата добавления: 2014-12-26