Нормальный закон распределения

Нормальный закон распределения и другие виды распределений

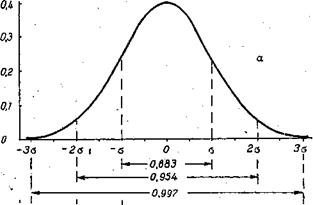
Нормальный закон[4] распределения во всех естественных науках имеет фундаментальное значение. И в психологических дисциплинах его значение трудно переоценить. Достаточно сказать, что все психологические шкалы основываются на этом законе, поскольку ему следуют распределения большинства человеческих способностей и свойств.

Рис. 14. Кривая нормального распределения

Самой общей характеристикой нормального распределения является простое наблюдение того закономерного факта, что очень большие центральные отклонения (x_i–M) встречаются крайне редко, а маленькие часто, при этом одинаковые по модулю отклонения одинаково вероятны. Такая закономерность может иметь место в условиях, когда на случайную величину х_i действует большое число разнообразных факторов и доля воздействия каждого из них одинаково мала по сравнению с их числом.

Свойства нормального распределения:

1. При всех значениях переменной х_i плотность положительна.

2. Плотность симметрична относительно математического ожидания, которое в этой связи нередко называют центром рассеивания (для симметричных распределений). Коэффициент асимметрии равен нулю.

3. При увеличении модуля аргумента кривая сколь угодно близко приближается к оси абсцисс, не достигая ее.

4. Численные значения среднего арифметического, моды и медианы совпадают.

5. Плотность нормального распределения быстро убывает по мере увеличения значений центрированной случайной величины, выраженных в единицах стандартного отклонения. Следует запомнить, что 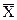± σ = 0,683; 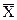± 2σ = 0,954; 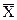± 3σ = 0,997.

6. При значениях – σ и + σ на кривой стандартной плотности на кривой дифференциального распределения) имеются точки смены кривизны (перегиба): на участке (– σ ≤ Х ≤ + σ) функция плотности вогнута вниз, а за его пределами, наоборот, вогнута вверх.

Несмотря на то, что теоретически нормальный закон распределения предполагает существование бесконечно малых и бесконечно больших значений любой, следующей ему величины, на практике (тем более в психологии) случайные переменные имеют конечные области существования. Поэтому на практике используются функции нормального распределения, ограниченные слева и справа основными отклонениями: ± 4.

Дата добавления: 2014-12-26