Меры изменчивости, или меры рассеивания

Дисперсия(Variance) — 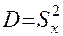— это средний квадрат отклонений всех значений признака от среднего арифметического. Имеет размерность значения признака в квадрате. Находится по следующим формулам:

А) при небольшом количестве испытуемых

, где

D — дисперсия

x_i — i-тое значение признака x

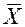— среднее арифметическое

i — номер испытуемого в выборке

N — число испытуемых или объем выборки

Б) для простого вариационного ряда (для каждого значения признака указана частота его появления в данной выборке)

, где

D — дисперсия

x_i — i-тое значение признака x

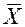— среднее арифметическое

m — число значений признака, встретившихся в данной выборке

i — номер значения признака по порядку

f_i — абсолютная частота каждого i-того значения признака x

N — число испытуемых или объем выборки

В) для сгруппированного распределения находится приближенное значение дисперсии по следующей формуле

, где

D — дисперсия

x_{ср i} — среднее значение каждого i-того интервала

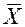— среднее арифметическое

k — число интервалов в сгруппированном ряду

i — номер интервала по порядку

f_i — абсолютная частота каждого i-того интервала

N — число испытуемых или объем выборки

Алгоритм вычисления дисперсии в сгруппированном распределении:

1. Для каждого интервала вычисляем его центральное отклонение по формуле x_срi –

2. Каждое центральное отклонение возводится в квадрат: (x_срi – )²

3. Находим произведение квадрата центрального отклонения каждого интервала и абсолютной частоты этого интервала (x_срi – )²· f_i

4. Находим сумму этих произведений ∑(x_срi – )²· f_i

5. Вычисляем среднее арифметическое значение как частное от деления ∑(x_срi – )²· f_i на N.

6. Находим дисперсию как частное отделения этой суммы на (N–1).

Для расчетов удобно выполнять каждое действие в отдельном столбце следующей таблицы:

Таблица 8

№ п/п	Xi (начало и конец интервалов)	fi	Fi	Xср i
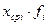
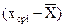
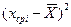
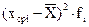
		S=N			S=……			S=………

Стандартное отклонение(или среднеквадратическое отклонение) (Std. deviation) — 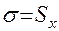— это среднее отклонение каждого значения признака от среднего арифметического. Имеет ту же размерность, что и сам признак. Находится по формуле: 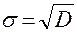, где D — дисперсия

Или, если в эту формулу подставить формулу дисперсии, то по следующим формулам:

А) при небольшом количестве испытуемых

, где

s — стандартное отклонение

x_i — i-тое значение признака x

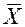— среднее арифметическое

i — номер испытуемого в выборке

N — число испытуемых или объем выборки

Б) для простого вариационного ряда (для каждого значения признака указана частота его появления в данной выборке)

, где

s — стандартное отклонение

x_i — i-тое значение признака x

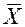— среднее арифметическое

m — число значений признака, встретившихся в данной выборке

i — номер значения признака по порядку

f_i — абсолютная частота каждого i-того значения признака x

N — число испытуемых или объем выборки

В) для сгруппированного распределения находится приближенное значение дисперсии по следующей формуле

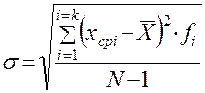, где

s — стандартное отклонение

x_{ср i} — среднее значение каждого i-того интервала

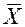— среднее арифметическое

k — число интервалов в сгруппированном ряду

i — номер интервала по порядку

f_i — абсолютная частота каждого i-того интервала

N — число испытуемых или объем выборки

Коэффициент асимметрии(Skewness) — As — параметр, характеризующий асимметричность распределения по сравнению с нормальным распределением. У симметричного распределения As=0.

При левосторонней асимметрии график сдвигается ближе к оси ординат, т. е. чаще встречаются более низкие значения признака. Коэффициент асимметрии в этом случае бывает положительным.

При правосторонней асимметрии график отодвигается от оси ординат, т. е. чаще встречаются более высокие значения признака. Коэффициент асимметрии в этом случае меньше нуля, отрицательный.

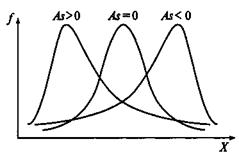
Рис.12. Распределения частот с разными значениями асимметрии

Коэффициент асимметрии находится по следующей формуле:

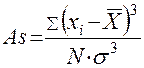, где

As— коэффициент асимметрии

x_i — i-тое значение признака x

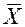— среднее арифметическое

N — число испытуемых или объем выборки

s — стандартное отклонение

Коэффициент эксцесса(Kurtosis) — Ex — параметр, характеризующий выпуклость распределения по сравнению с нормальным распределением. В распределениях с нормальной выпуклостью Ex=0.

В тех случаях, когда в выборке встречается много средних или близких к средним значений, распределение имеет вид островершинной кривой. Коэффициент эксцесса в этом случае положительный, т. е. больше нуля.

Если же в распределении преобладают крайние значения, причем одновременно и более низкие, и более высокие, то такое распределение имеет вид низкой, плосковершинной кривой, или иногда низкой кривой с двумя вершинами. Коэффициент эксцесса — отрицательный.

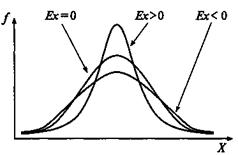
Рис.13. Распределения частот с разными значениями эксцесса

Коэффициент эксцесса находится по следующей формуле

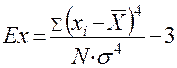, где

Ex— коэффициент эксцесса

x_i — i-тое значение признака x

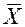— среднее арифметическое

N — число испытуемых или объем выборки

s — стандартное отклонение

Коэффициент вариацииили коэффициент вариативности— V — параметр, показывающий соотношение стандартного отклонения и среднего арифметического. Применяется для сравнения изменчивости распределений признаков, имеющих разную размерность, то есть сам коэффициент вариации является безразмерной мерой рассеивания.

Находится по формуле:

, где

V — коэффициент вариации

s — стандартное отклонение

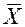— среднее арифметическое

Коэффициент вариации позволяет сравнивать изменчивость признаков, измеренных по разным шкалам, а также оценивать однородность выборки (для однородных выборок он должен быть не более 30%).

Дата добавления: 2014-12-26