Основы гидродинамики

6.1. ОСНОВНЫЕ ПОЛОЖЕНИЯ

Задачи гидродинамики делятся на два основных класса: внутренние и внешние. К внешним задачам относятся задачи обтекания тела потоками жидкости или газа, или о движении тела в жидкой или газообразной среде. Внешними задачами являются задачи, связанные с полётами самолётов, снарядов и других тел, движущихся в атмосфере. Внутренние задачи занимаются движением жидкости в каналах. В этот класс задач входят такие как:

· течение жидкостей в трубопроводах (водопровод, газо-и нефтепроводы, кровеносная система, тепло и газоснабжение);

· течение воды в открытых каналах и реках (ирригационные и осушительные системы, расчёт паводков, судопропускные сооружения и т.д.).

При решении внешней задачи основной акцент делается на определение силового взаимодействия потока и тела. Определение силы, действующей со стороны набегающего потока, или силы сопротивления движению тела в жидкости - цель таких задач. Поэтому при анализе и решении внешних задач, как правило, используются уравнения, выражающие закон изменения количества движения: дифференциальные уравнения Навье - Стокса или Рейнольдса, а также интегральные формы этого закона.

При решении внутренней задачи чаще всего стараются определить потери энергии в потоке жидкости. Здесь используются уравнения, выражающие закон изменения кинетической энергии, чаще всего в виде различных форм уравнения Бернулли.

В основе гидродинамики, как части гидромеханики, положены четыре основных закона механики:

· закон сохранения массы;

· закон изменения количества движения (импульса);

· закон изменения момента количества движения;

· закон изменения кинетической энергии.

Эти законы формулируются для конечных объёмов (размеры ограничены и оговорены). Законы гидродинамики для конечных объёмов часто упрощаются с учётом конкретных условий на поверхностях, ограничивающих данный объём. Такие упрощенные уравнения используются в разделе, называемом гидравликой. По сути это теоретические основы технической механики жидкости. Они особенно эффективны, когда исследуются интегральные (осреднённые по времени и пространству) гидромеханические характеристики потоков.

В том случае, когда есть необходимость определять гидромеханические характеристики и величины в каждой точке объёма жидкости, используют дифференциальные уравнения. Они тоже являются фундаментальными законами механики, но относятся к точке сплошной среды. Если эти уравнения дополнить каким-либо реологическим законом, то можно определить структуру поля скорости и напряжённое состояние в любой точке потока жидкости.

Практическое использование этих уравнений, в зависимости от изложенных здесь подходов, преобразуется из одного вида в другой с помощью теоремы Остроградского - Гаусса. Так при выводе гидравлических уравнений объёмные интегралы заменяются на поверхностные с тем, чтобы использовать особенности условий на поверхностях, ограничивающих поток, для упрощения уравнений. При выводе дифференциальных уравнений, наоборот, поверхностные интегралы заменяются на объёмные, чтобы можно было исследовать гидромеханические величины в точках внутри потока. При этом условия на границах потока вводятся как граничные или краевые условия для дифференциальных уравнений.

6.2.ЗАКОН СОХРАНЕНИЯ МАССЫ

Выделим в пространстве контрольный объём V, ограниченный произвольной контрольной поверхностью А. Пусть плотность жидкости r зависит и от времени, и от координат, т.е. .

Масса бесконечно малого объёма dV, расположенного в точке с координатами , в момент времени t равна . Масса объёма V жидкости, находящейся внутри замкнутой поверхности А, равна

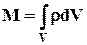. (6.2.1)

Согласно закону сохранения массы, при движении жидкого объёма его масса остаётся неизменной. Изменение во времени гидромеханической характеристики, относящейся к движущемуся жидкому объёму, который содержится в начальный момент внутри контрольной поверхности А, выражается в виде субстанциональной производной от этой характеристики. Представим закон сохранения массы, используя эту производную

. (6.2.2)

Уравнение (6.2.2) используют в качестве уравнения неразрывности при решении одномерных задач, а также в виде дифференциальных уравнений, когда контрольный объём бесконечно мал.

6.3. ЗАКОН ИЗМЕНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ

Изменение количества движения жидкого объёма за единицу времени равно сумме всех приложенных к нему внешних (массовых и поверхностных) сил. Количество движения и силы - величины векторные, поэтому уравнение, выражающее этот закон, является векторным. Ему соответствует система трёх уравнений, связывающих проекции векторов на оси координат.

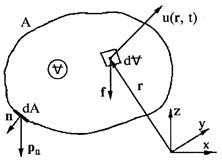  Рис.6.1. К выводу уравнения количества движения

Выделим в пространстве объём жидкости V и ограничим его контрольной поверхностью А (рис.6.1). Бесконечно малый объём dV имеет массу rdVи количество движения rudV. Количество движения всего объёма равно . Изменение количества движения при перемещении этого объёма за единицу времени составит

. (6.3.1)

Вектор внешних массовых сил, плотность распределения которых обозначим через f (х,у,z), находим аналогично: на элементарный объём dV массой rdV действует сила frdV, следовательно, внешняя массовая сила, действующая на весь объём V, равна

. (6.3.2)

Плотность распределения внешней поверхностной силы (напряжение) на контрольной поверхности А обозначим через p_n, учитывая, что n - нормаль к А. Тогда на элементарную площадку dA действует сила p_n dA, а на всю поверхность действует результирующая поверхностная сила

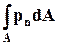. (6.3.3)

Приравняв изменение количества движения (6.3.1) сумме сил (6.3.2) и (6.3.3), получим уравнение, выражающее закон изменения количества движения:

. (6.3.4)

Это векторное уравнение равносильно трём скалярным уравнениям, которое можно записать, проектируя все слагаемые на координатные оси х,у,z. Например, в проекции на ось х имеем

. (6.3.5)

Уравнение (6.3.4) используется и в приведённом выше виде в виде гидравлического уравнения количества движения или в виде систем дифференциальных уравнений, получаемых из (6.3.4), когда контрольный объём V бесконечно мал.

6.4.ЗАКОН ИЗМЕНЕНИЯ МОМЕНТА КОЛИЧЕСТВА

ДВИЖЕНИЯ

Изменение момента количества движения жидкого объёма относительно некоторой точки за единицу времени равно сумме моментов всех внешних (массовых и поверхностных) сил, действующих на этот объём, относительно той же точки. По определению момент вектора 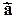(рис.4.2) относительно, например, начала координат равен

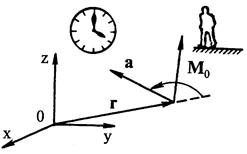  Рис.6.2. Момент вектора

, (6.4.1)

где r радиус-вектор, определяющий точку приложения вектора а. Вектор М₀ направлен по нормали к плоскости, определяемой векторами а и r, так, что, глядя с конца вектора М₀, видим поворот от вектора r к вектору а, происходящим против часовой стрелки. Модуль вектора М₀ равен

.

В матричной форме векторное произведение записывается в виде

или

, (6.4.2)

т.е. проекции вектора М₀ на координатные оси численно равны записанным определителям.

Запишем закон изменения момента количества движения по аналогии с уравнением закона изменения количества движения. С этой целью каждый вектор уравнения (6.3.4) умножим векторно на r (слева):

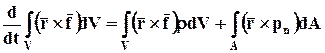. (6.4.3)

Полученное векторное уравнение эквивалентно трём скалярным уравнениям, которые можно выписать, проецируя слагаемые, входящие в уравнение (6.4.3), на координатные оси. Например, в проекции на ось z имеем

. (6.4.4)

Интегральная форма уравнения (6.4.3) используется главным образом в гидромашиностроении при расчётах вращающихся рабочих колёс турбин и насосов.

6.5. ЗАКОН ИЗМЕНЕНИЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ

Изменение кинетической энергии жидкого объёма за единицу времени равно мощности всех внешних и внутренних (поверхностных и массовых) сил, действующих на этот объём жидкости. Кинетическая энергия бесконечно малого объёма dV жидкости равна 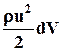, тогда кинетическая энергия конечного объёма V будет равна

. (6.5.1)

Мощность силы равна скалярному произведению вектора силы и скорости тела, на которое она действует. Например, на элементарный объём dV действует внешняя массовая сила с плотностью распределения f, величина этой силы равна frdV. Работа этой силы на перемещении 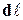равна

.

Мощность силы найдём как отношение совершаемой ею работы ко времени dt, за которое произойдёт перемещение объёма dV на расстояние 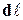. При этом скорость жидкого объёма dV равна . Следовательно, мощность внешней объёмной силы для элементарного объёма dV равна 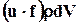. Мощность этой силы при перемещении всего объёма V

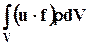. (6.5.2)

Рассуждая аналогично, найдём мощность внешних поверхностных сил, действующих на поверхность А, ограничивающую объём V:

, (6.5.3)

где u - скорость жидкости на поверхности А в точке, где выделен элемент dА.

Рассчитать работу внешних сил, как правило, не представляется возможным, так как она зависит от поля скорости внутри контрольного объёма, которое неизвестно. Поэтому введём функцию 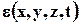- плотность распределения мощности внутренних сил, т.е. работы, которая за единицу времени переходит в тепло и рассеивается (диссипирует) внутри объёма жидкости, имеющего единичную массу. Работа внутренних сил может только уменьшать кинетическую энергию, так как, переходя в энергию беспорядочного теплового движения молекул, соответствующая часть кинетической энергии объёма V уже не участвует в дальнейшем балансе механической энергии. Обычно мощность внутренних сил называют диссипированной, а функцию e диссипативной. Уменьшение кинетической энергии объёма V за счёт работы внутренних сил представим в виде

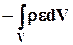. (6.5.4)

Знак минус вводится, чтобы функция e (х,у,z,t) была всегда положительной.

Приравнивая субстанциональную производную от кинетической энергии (6.5.1) сумме мощностей (6.5.2),(6.5.3) и (6.5.4), получаем уравнение, выражающее закон изменения кинетической энергии:

. (6.5.5)

Если уравнение (6.5.5) используют для решения одномерных задач, то его представляют в виде различных модификаций уравнения Бернулли. Закон изменения кинетической энергии в виде дифференциального уравнения не используется, так как оно эквивалентно дифференциальному уравнению, выражающему закон изменения количества движения.

6.6. ОБЩИЙ ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ ДЛЯ

КОНТРОЛЬНОГО ОБЪЁМА СПЛОШНОЙ СРЕДЫ

В дополнение к закону изменения кинетической энергии, выражающему баланс механической энергии, рассмотрим более общий случай, принимая во внимание изменение механической энергии за счёт её источников (стоков), содержащихся внутри контрольного объёма, и баланс внутренней энергии (тепла).

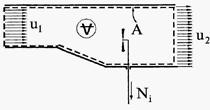Рис.6.3. Контрольный объём для формулировки закона сохранения энергии

Пусть в контрольном объёме V, который выделен на рис. 6.3. контрольной поверхностью А, указанной штриховой линией установлена турбина, которую вращает набегающий поток, отдавая ей мощность N_i (поток совершает работу N_i в единицу времени). Индекс i означает, что устройств, изменяющих механическую энергию потока, может быть несколько. Если вместо турбины установить насос, то соответствующая мощность насоса увеличит механическую энергию потока, так что знак N_i зависит от функции устройства внутри контрольного объёма. Запишем при этом уравнение, выражающее баланс механической энергии:

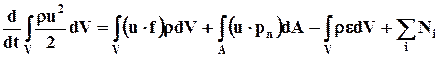. (6.6.1)

Рассмотрим баланс тепла в контрольном объёме. Пусть Е - количество внутренней энергии жидкости (теплоты) внутри контрольного объёма, а е(r,t) - плотность её распределения в пространстве, т.е. удельная внутренняя энергия жидкости (на единицу массы). Тогда

. (6.6.2)

Чем могут быть вызваны изменения внутренней энергии жидкости внутри контрольного объёма? Возможны следующие причины:

· наличие внутри объёма источников тепла, подводимого извне, с плотностью распределения t (r,t) (на единицу объёма в единицу времени);

· присутствие на граничных поверхностях источников тепла с плотностью распределения s(r,t) (на единицу площади в единицу времени);

· работа внутренних сил в жидкости, например, за счёт вязкости; плотность распределения мощности внутренних сил e(r,t).

Баланс тепла для жидкости, содержащейся в контрольном объёме в момент времени t, имеет вид

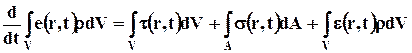. (6.6.3)

Складывая (6.6.1) и (6.6.3), получаем уравнение, выражающее общий закон сохранения энергии для контрольного объёма сплошной среды (6.6.4):

.

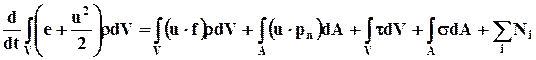Как следует из (6.6.4), работа внутренних сил не изменяет полную энергию системы жидких частиц: она уменьшает механическую энергию и увеличивает тепловую.

6.7. УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ

Основным динамическим уравнением движения материальной точки является 2-й закон Ньютона m` a = `F, а широко используемым следствием этого закона являются следующие общие теоремы движения системы материальных точек:

· производная по времени от количества движения

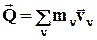
равна сумме всех действующих на систему внешних сил

(6.7.1)

и называется уравнением количества движения, или уравнением импульсов:

· производная по времени от кинетического момента

системы относительно какого-либо неподвижного центра О равна сумме моментов

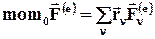
всех внешних сил, действующих на систему, относительно того же центра, т.е.

, (6.7.2)

называется уравнением моментов количества движения;

· дифференциал кинетической энергии

системы равен сумме элементарных работ

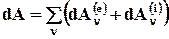
всех действующих на систему внешних и внутренних 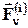сил, т.е.

(6.7.3)

называется уравнением механической энергии (теоремой живых cил).

· Для любого мысленно выделяемого индивидуального объёма сплошной среды V, ограниченного поверхностью S, уравнения (1.68) - (1.70) действительны, если динамические величины определить следующим образом:

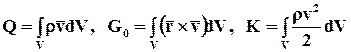
(соответственно количество движения, момент количества движения и кинетическая энергия сплошной среды в объёме V);

(соответственно сумма внешних объёмных и поверхностных сил и их моментов относительно некоторого неподвижного центра О, действующих на среду в объёме V). Силы и их моменты непрерывно определены и сосредоточены.

Сумма элементарных работ внешних и внутренних объёмных и поверхностных сил

.

В этом случае уравнения (6.7.1) и (6.7.2) являются основными постулируемыми динамическими соотношениями механики сплошной среды. Они служат исходными уравнениями для описания любых движений сплошной среды, в том числе разрывных движений и ударных процессов.

Уравнение (6.7.3) одно из наиболее важных следствий уравнений (6.7.1) и (6.7.2) при непрерывных движениях в пространстве и времени.

При непрерывных движениях интегральная теорема движения (6.7.1) эквивалентна следующим 3 дифференциальным уравнениям:

· в декартовой системе координат:

· в цилиндрической системе координат при осевой симметрии

(6.7.4)

где проекции ускорения вычисляют по формулам (1.6).

Эти уравнения, связывающие компоненты v_i вектора скорости и тензора напряжений 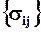, являются основной системой дифференциальных уравнений движения для любой сплошной среды, представляющих собой уравнение баланса количества движения (импульса) для бесконечно малого объёма среды. Если движения частиц происходят без ускорения (а_i = 0) или они пренебрежимо малы, то уравнения (6.7.4) называются дифференциальными уравнениями равновесия.

При непрерывном движении сплошной среды теорема моментов количества движения (6.7.2) в дифференциальной форме сводится к выводу о том, что тензор напряжений симметричен, т.е. s_ij = s_ji. Если тензор напряжений симметричен, то уравнения моментов количества движения удовлетворяются тождественно.

Интегральная теорема живых сил (6.7.3) эквивалентна следующему дифференциальному уравнению:

dK = dW = dA^(e), (6.7.5)

где

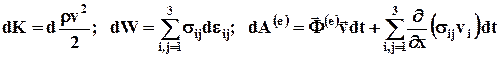
соответственно изменение кинетической и потенциальной энергии бесконечно малого объёма сплошной среды, элементарная работа внешних объёмных и поверхностных сил, действующих на бесконечно малый элемент объёма среды.

Уравнение (6.7.5) является следствием уравнения движения(6.7.4) и представляет собой уравнение баланса механической энергии.

В общем случае оно не является законом сохранения энергии, но его можно так трактовать тогда, когда механическая энергия тела не переходит в тепловую или другие виды энергии. Общий закон сохранения энергии в этом случае распадается на два:

· закон сохранения механической энергии;

· закон сохранения энергии другого вида.

Дата добавления: 2014-12-26