Основы реологии 1 страница

ЗАДАЧ

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РЕШЕНИЯ ОДНОМЕРНЫХ

7.1. ОСНОВНЫЕ ТЕРМИНЫ И ПОНЯТИЯ

Одномерное приближение - весьма эффективный способ описания движения жидкости в случае, если продольные (измеренные вдоль на­правления движения) размеры потока во много раз превосходят его по­перечные размеры, что характерно главным образом для движения жид­кости в трубах, реках и каналах.

Важной особенностью потоков в трубах и каналах является то, что неподвижные твердые границы (стенки трубопроводов, дно рек и кана­лов) составляют значительную часть поверхности, ограничивающей по­ток. На этих границах выполняется условие прилипания, т.е. на них ско­рость жидкости u_гр = 0 (равны нулю и нормальная к границе и касатель­ная к ней составляющие). Благодаря этому на тех границах контрольного объема V, которые совпадают с твердыми границами потока, поверхнос­тные интегралы, входящие в фундаментальные законы гидромеханики и содержащие скорость u или ее проекции, обращаются в ноль. Это существенно упрощает получение расчетных зависимостей, основан­ных на фундаментальных законах.

В достаточно длинных цилиндрических или призматических трубах и каналах формируются потоки жидкости с линиями тока, параллельными твердым границам, в которые заключен поток. Движение жидкости, при котором линии тока представляют собой параллельные прямые, будем на­зывать равномерным, или параллельно-струйным.

Поперечное сечение потока, ортогональное линиям тока, называют живым сечением. При равномерном движении жидкости живое сечение плоское. Благодаря этому, в частности, исключается необходимость ис­следовать поле скорости и появляется возможность оперировать сред­ним по сечению значением скорости.

Это связано с тем, что вектор скорости u (как и линия тока) перпен­дикулярен к живому сечению и проекция скорости на нормаль к этому сечению u_n равна модулю скорости:

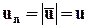. (7.1.1)

Кроме того, при равномерном дви­жении справедливы два следующих утверждения (леммы}.

1. Нормальное напряжение р_nn в каждой точке живого сечения равно
гидродинамическому давлению р в этой точке со знаком минус (так как
положительным считается растягивающее нормальное напряжение):

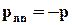. (7.1.2)

2. Гидродинамическое давление р в живом сечении распределено по
гидростатическому закону

pU - p = const, (7.1.3.)

где U - потенциал внешней массовой силы; р - плотность жидкости.

При неравномерном движении жидкости, когда линии тока непарал­лельны и (или) криволинейны, различают:

· плавноизменяющееся движение, при котором можно пренебречь кри­визной линий тока и их непараллельностью и с достаточной для практических целей точностью построить плоское живое се­чение, допуская, что в нем выполняются условия (7.1.1), (7.1.2) и (7.1.3);

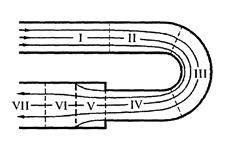Рис.7.1. Равномерное, плавноизменяющееся и резкоизменяющееся движение жидкости

· резкоизменяющееся движение, при котором нельзя использовать ука­занные условия.

Для иллюстрации рассмотрим течение в трубопроводе, представ­ленное на рис. 7.1.

На длинных цилиндрических участках I и VII движение равномер­ное, линии тока параллельны обра­зующим стенок трубы.

На криволинейном участке III движение резкоизменяющееся, здесь хотя и можно построить плоские живые сечения, но в них не будут выполняться условия (7.1.2) и (7.1.3).В частности, вследствие действия центробежных сил, обусловленных кривизной линий тока, давление в плоских живых сечениях не будет распределено по гидростатическому закону (7.1.3).

На участке V движение резкоизменяющееся; здесь живое сечение (ортогональное линиям тока) сильно искривлено, так что даже вычисле­ние его площади является непростой задачей, кроме того, вследствие зна­чительной кривизны линий тока в этих сечениях не выполняются условия (7.1.2) и (7.1.3).

На участках II, IV и VI движение неравномерное, но в пределах этих участков можно с достаточной точностью и построить плоское живое сечение, и допустить выполнение равенств (7.1.2) и (7.1.3).

Задачи механики жидкости и газа, основанные на использовании при­веденных выше понятий (плоское живое сечение, равномерное и плавно-изменяющееся движение и др.), называются одномерными.

В технической механике жидкости (гидравлике) потоки разделяют на на­порные, безнапорные и струйные. Если поток со всех сторон ограничен твер­дыми стенками, то он называется напорным (например, поток воды в водопро­водных трубах). Если только часть потока ограничена твердыми стенками, а на остальной части жидкость граничит с газом (в частности, с атмосферой), т.е. ограничена свободной поверхностью, то такое движение называется безна­порным (например, потоки в реках, каналах). Если же поток не ограничен твердой поверхностью, то он называется струйным, или просто струей. Струя жидкости может быть ограничена той же самой жидкостью (затопленная струя) или газом (струя воды в воздухе).

7.2. УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ УСТАНОВИВШЕГОСЯ НАПОРНОГО ПОТОКА ВЯЗКОЙ ЖИДКОСТИ

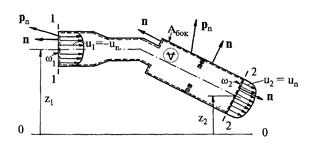Рис. 7.2. Контрольный объём для вывода уравнения Бернулли

Уравнение Бернулли для установившегося потока вязкой жидкости является выражением закона изменения кинетической энергии приме­нительно к одномерным задачам гидромеханики. Выделим в трубопрово­де (рис. 7.2) сечениями 1-1 и 2-2, в которых движение равномерное или плавноизменяющееся контрольный объем V, ограниченный контрольной поверхностью А, показанной штриховой линией. Запишем для выделен­ного объема V закон изменения кинетической энергии:

. (7.2.1)

Преобразуем слагаемые, входящие в это уравнение, представляя объем­ные интегралы в виде поверхностных и используя условия на контрольной поверхности А, которую запишем в виде сум­мы А = w₁ + w₂ +А_бок.

1. В субстанциальной производной

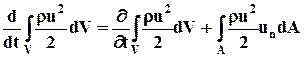(7.2.2)

первое слагаемое равно нулю, так как движение жидкости установивше­еся и жидкость несжимаема (r= const), а второе слагаемое представляет собой поток кинетической энергии Q_k через контрольную поверхность А. Условия на контрольной поверхности А имеют вид (рис. 7.2)

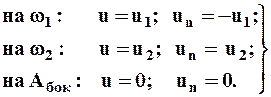(7.2.3)

Преобразуем второе слагаемое в (7.2.2), используя (7.2.3), (5.11) и (5.27):

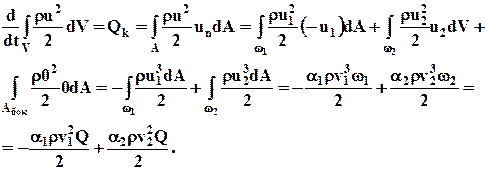(7.2.4)

2. Обратимся в уравнении (7.2.1) к слагаемому, выражающему мощность внешней массовой силы. Предположим, что внешняя массовая сила имеет потенциал, т.е. существует такая скалярная функция U, для кото­рой f = gradU. Используя теорему Остроградского - Гаусса и граничные условия (7.2.3), получаем

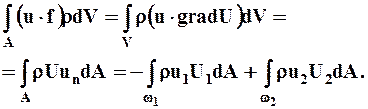(7.2.5)

Полученное равенство позволяет выразить мощность внешней мас­совой силы через поток потенциальной энергии, обусловленной этой силой, сквозь живые сечения.

3. Рассмотрим интеграл, выражающий мощность внешней поверхно­стной силы:

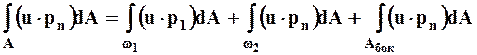. (7.2.6)

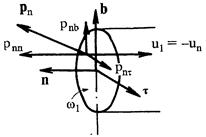Рис.7.3. Напряжение и скорость жидкости в поперечном сечении w₁

В сечении 1 - 1 скорость имеет только нормальную составляющую u_n, так как движение здесь равномерное или плавноизменяющееся. Чтобы вы­числить скалярное произведение u • р_n, зададим в произвольной точке живого сечения w₁ систему ортогональных координат (рис. 7.3), определяе­мую тремя единичными векторами (n, b, t), из которых n - нормален к живому сечению, a b и t лежат в его плоскости. Проектируя на эти коор­динатные оси векторы u и р_n, находим

u = (u_n, u_b,u_t) = (u_n, 0, 0); р_n = (p_nn, p_nb, р_пt),

при этом все три проекции напряжения р_n могут быть отличны от нуля. По определению скалярного произведения

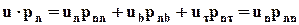. (7.2.7)

Аналогичные вычисления выполним для живого сечения w₂. На поверхности А_бок выполняется условие прилипания. Согласно полученным результатам, а также используя (7.1.2), на контрольной поверхности А имеем условия:

(7.2.8)

Подставляя (7.2.8) в (7.2.7) и в (7.2.6), получаем

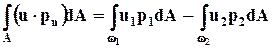. (7.2.9)

Согласно равенству (7.2.9) мощность внешней поверхностной силы можно интерпретировать как поток, обусловленный этой силой потен­циальной энергии сквозь живое сечение; в соответствии с (3.13) плот­ность распределения этой энергии равна давлению р.

Сложим равенства (7.2.5) и (7.2.6) и найдем выражение для мощности внешних сил, которое в соответствии с вышеизложенным будем интер­претировать как поток потенциальной энергии Q_p, обусловленный внеш­ними массовой и поверхностной силами через контрольную поверхность:

.

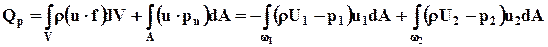Примем во внимание, что в сечениях 1 - 1 и 2 - 2 движение равно­мерное или плавноизменяющееся, и, следовательно, согласно (7.1.3) дав­ление в этих сечениях распределено по гидростатическому закону: rU - р = const.

В соответствии с этим выражение в скобках в интегралах по живым сечениям можно вынести за знак интеграла. Кроме того, положим, что сила тяжести является единственной внешней массовой силой, т.е., что U = - g z. В результате получим

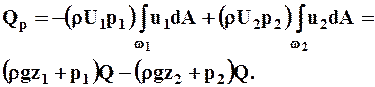^. (7.2.10)

4. Последнее слагаемое в (7.2.1), выражающее мощность внутренних сил в пределах контрольного объема, оставляем без преобразования.

Подставив (7.2.4) и (7.2.10) в исходное уравнение (7.2.1) и разделив все слагаемые на весовой расход Q_B = rgQ, получим искомое уравнение Бернулли:

, (7.2.11)

где g = rgQ удельный вес, а слагаемое

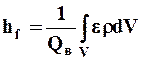(7.2.12)

выражает отнесенную к весовому расходу мощность внутренних сил (дис­сипацию механической энергии в единицу времени) в пределах конт­рольного объема.

Для сжимаемой жидкости (газа) можно выполнить аналогичный вы­вод и получить уравнение Бернулли в виде

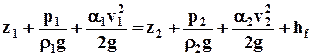, (7.2.13)

где r₁ и r₂ - плотности жидкости (газа) в сечениях 1 - 1 и 2 - 2.

7.3. ГЕОМЕТРИЧЕСКАЯ И ЭНЕРГЕТИЧЕСКАЯ ИНТЕРПРЕТАЦИИ СЛАГАЕМЫХ, ВХОДЯЩИХ В УРАВНЕНИЕ БЕРНУЛЛИ

Обратимся к интерпретации отдельных слагаемых, входящих в урав­нение Бернулли для несжимаемой (капельной) жидкости (r = const). Го­ризонтальная координатная плоскость хОу, от которой отсчитывается ко­ордината z при решении гидравлических задач, называется плоскостью сравнения и обозначается на чертежах 0 - 0. Из вывода уравнения (7.2.11) следует, что z - это координата произвольной точки живого сечения w, а р - это гидродинамическое давле­ние в этой же точке. Из гидростати­ки известно, что отношение p/rg рав­но высоте столба жидкости, который создает давление, равное р.

Чтобы исключить возмущения потока, измерительные открытые трубки присоединяют к точкам жи­вого сечения, совпадающим с грани­цей потока (рис. 7.4).

Рис.7.4. Геометрическая интерпретация слагаемых, входящих в уравнение Бернулли

С учетом изложенного выше можно дать следующую геометричес­кую интерпретацию слагаемых, вхо­дящих в уравнение Бернулли:

z - превышение над плоскостью сравнения (геодезическая отметка) любой точки живого сечения потока;

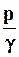- пьезометрическая высота в этой же точке, т.е. высота, на

которую поднимается вода в открытой трубке, присоединенной к этой точке;

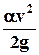- всегда положительна и имеет размерность длины;

в соответствии с уравнением (7.2.11) эту величину откладывают вверх от отметки .

Кроме того, можно дать энергетическую интерпретацию слагаемых, входящих в уравнение Бернулли:

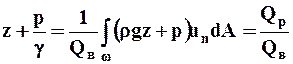- отношение потока потенциальной энергии (обусловленного течением жидкости) через живое сечение к ве­совому расходу;

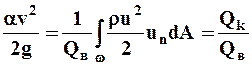- отношение потока кинетической энергии поступательного движения жидких частиц через сечение к весовому расходу;

- мощность (механическая энергия в единицу

времени), которая переходит в тепло внутри объема V, т.е. в трубопро­воде между сечениями 1 - 1 и 2 - 2, другими словами, диссипированная мощность, отнесенная к весовому расходу.

7.4. ПОТЕНЦИАЛЬНЫЙ И ПОЛНЫЙ (ГИДРОДИНАМИЧЕСКИЙ) НАПОРЫ. ПЪЕЗОМЕТРИЧЕСКАЯ И НАПОРНАЯ ЛИНИИ

Удельные потоки энергии, т.е. обусловленные движением жидкости потоки энергии через живое сечение, отнесенные к весовому расходу жид­кости, называют напорами.

Введем понятия

· потенциальный напор ; (7.4.1)

· скоростной напор 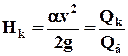; (7.4.2)

· полный, или гидродинамический напор

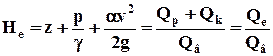; (7.4.3)

· потеря напора между сечениями 1 - 1 и 2 - 2

. (7.4.4)

Принимая такие обозначения, запишем уравнение Бернулли в виде

. (7.4.5)

При решении задач о движении в трубах и каналах часто, задав плоскость сравнения в каждом живом сечении потока, определяют потенциальный и полный напоры и указывают геометрическое место точек, отвечающих этим напорам, в соответствии с их геометрической интерпретацией (рис. 7.5).

Если в каждом живом сечении отложить от плоскости сравнения по вертикали величину потенциального напора 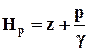, то совокупность точек образует пьезометрическую линию Р - Р, которую будем показывать пунктиром. Аналогично, если в каждом сечении отложить по вертикали от плоскости сравнения величину полного напора

, то со­вокупность точек образует напорную линию Е - Е, показываемую сплош­ной линией.

Рис. 7.5. Пьезометрическая Р - Р и напорная Е - Е линии

Отметим, что понятие напора было введено для тех сечений потока, где движение равномерное или плавноизменяющееся. На участке, где движение резкоизменяющееся (например, между сечениями а - а и b - b на рис. 7.5), напорная и пьезометрическая линии строятся условно путем их экстраполяции из областей, где движение плавноизменяющееся.

На участке с равномерным движением (например, между сечениями 1 -1 и а - а) потери напора потока на каждую единицу длины будут одина­ковы (структура потока во всех сечениях одинакова, следовательно, и ра­бота всех внутренних сил, определяющих потерю напора, в одинаковых объемах будет одинакова), поэтому напорная линия Е - Е на таких участ­ках будет прямой. Пьезометрическая линия, которая располагается всегда ниже напорной на величину 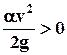, будет прямой, параллельной на­порной линии. Важными характеристиками этих линий являются их продольные уклоны, т.е. отношение разности напоров на участке равно­мерного движения к расстоянию между сечениями, в которых эти напо­ры вычислены.

Уклон напорной линии называется гидравлическим и обозначается J_e, а уклон пьезометрической линии называется пьезометрическим и обо­значается J_p. Например, для участка потока между сечениями 1 - 1 и а - а

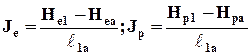. (7.4.5)

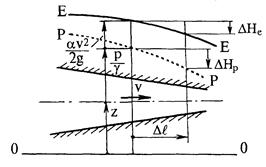Рис.7.6. Пьезометрическая Р - Р и напорная Е - Е линии при плавноизменяющемся движении

Если движение плавноизменяющееся, то и потери напора на каждой единице длины вдоль потока будут переменны, и скоростной напор будет меняться вдоль оси потока. При этом линии Е-Е и Р-Р будут кривыми (рис.7.6). В этом случае гидравлический и пьезо­метрический уклоны определяются для каждого сечения как уклоны на элементарном участке длиной , прилегающем к сечению, т.е. как ук­лоны касательной к соответствующим линиям:

; (7.4.6)

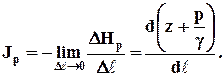(7.4.7)

Здесь знак минус показывает, что положительным считается уклон, при котором геодезические отметки линий Е - Е и Р - Р уменьшаются вдоль потока.

При равномерном движении (рис. 7.5)

. (7.4.8)

Следовательно, гидравлический уклон численно равен удельной (на единицу весового расхода) диссипированной мощности в объеме потока, приходящейся на единицу длины. В заключение отметим два важных положения.

1. Потери напора - величина положительная (механическая энер­гия жидкости при движении мо­жет лишь уменьшаться, переходя в тепло), поэтому полный напор в сечениях, расположенных ниже по течению, всегда меньше напора в сечениях, расположенных выше по течению. Отметки напорной линии вдоль потока все­гда уменьшаются, и гидравлический уклон всегда положителен (J_e > 0).

2. Если часть кинетической энергии жидкости при её движении переходит в потенциальную, то потенциальный напор может возрастать, при этом отметки пьезометрической линии возрастают.

8.1. УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНЫХ И РЕАЛЬНЫХ

ЖИДКОСТЕЙ

1. Простейшей механической моделью сплошной среды является модель идеальной жидкости, для которой характерно отсутствие сопротивления (сил трения) при скольжении одного слоя жидкости по другому. Отдельные части взаимодействуют только в виде нормального давления. То есть, В любой точке идеальной жидкости касательные напряжения равны 0, а нормальные s_II = -Р; (или через компоненты девиатора напряжений): S_ij = 0 (i, j = 1,2,3).

Уравнением состояния для идеальной жидкости служит зависимость плотности r от давления Р и температуры Т:

r = f (р,Т). (8.1.1)

Например, для идеального газа приемлемо уравнение Клапейрона -Менделеева: r = RTp.

Если плотность жидкости - функция только давления r = f(p), то жидкость называют баротропной.

Когда имеет место степенная зависимость r = срⁿ, то говорят, что движение происходит при политропическом процессе.

Для капельных жидкостей, сжимаемость для которых чрезвычайно мала, в большом диапазоне изменения давления связь между плотностью и давлением линейна: ,

r₀ - плотность, соответствующая давлению р₀, К_ж - модуль объёмного сжатия, порядок которого равен 10⁴nМПа.

Экспериментальные данные и общие физические представления показывают, что при больших температурах и давлениях любая среда практически обладает свойствами идеальной жидкости.

В нормальных условиях модель идеальной жидкости широко используется при изучении движения многих жидкостей и газов вдали от твёрдых границ.

Одно из наиболее известных уравнений движения идеальной жидкости - закон Бернулли:

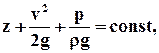
который гласит: При установившемся движении несжимаемой идеальной жидкости сумма геометрической, скоростной и пьезометрической высот вдоль линии тока остаётся величиной постоянной.

2. В тех случаях, когда силами трения или напряжения сдвига при движении жидкости пренебречь нельзя, используют следующую по сложности модель- вязкую ньютоновскую жидкость. Уравнениями состояния для такой жидкости, кроме уравнения (8.1.1), будет

s_ij = 2µl_ij (i, j = 1,2,3). (8.1.2)

Т.е. между компонентами девиатора напряжений и скоростей деформации существует прямо пропорциональная связь.

Или через компоненты тензоров напряжений и скоростей деформации

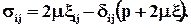
Например, при плоском слоистом течении жидкости вдоль оси Ох₁, когда v₁ = v₁(x₁, x₂), v₂ = v₃ = 0, нормальные и касательные напряжения равны

Если, кроме того, жидкость несжимаема (div v = 0) и скорость v₁ не зависит от x₁, то уравнение состояния имеет простейший вид

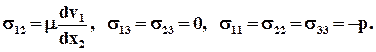
Коэффициент пропорциональности m называется коэффициентом вязкости или динамической вязкостью жидкости.

Размерность коэффициента динамической вязкости [m] = [(сила× длина):(длина² ×скорость)] = [сила×время/длина²]. В системе СИ единицей вязкости является паскаль-секунда 1Па×с = 1н×с/м². Величина 1 пуаз = 0.1 Па×с. Динамическая вязкость воды при 20°С равна 10^-3 Па×с.

Иногда пользуются отношением m/r, которое называется кинематической вязкостьюи обозначается буквой n. Размерность кинематической вязкости м²/с.

Для газов и капельных жидкостей динамическая и кинематическая вязкости слабо зависят от давления, но сильно от температуры: убывают с повышением температуры, а у воздуха - растут.

Таблица 8.1

Т°С
Вода, Па×с	1.792	1.005	0.656	0.469	0.357	0.284
Вода, м^2/с	1.792	1.007	0.661	0.477	0.367	0.296
Воздух, Па с	1.709	1.808	1.904	1.997	2.088	2.175
Воздух, м^2/с	0.132	0.150	0.169	0.188	0.209	0.230

Для учёта зависимости вязкости от температуры существует много различных эмпирических формул, но практики предпочитают пользоваться табличными значениями.

Свойствами ньютоновских жидкостей, описываемых уравнениями (8.1.2), обладает большинство чистых жидкостей и газов. Многие растворы, в том числе буровые и тампонажные, проявляют свойства, отличные от свойств ньютоновских жидкостей.

Вязкость неньютоновских жидкостей зависит не только от температуры и давления, но и от скорости сдвига, деформации, времени, характера движения.

3. Основной признак неньютоновского поведения жидкостейзаключается в нелинейном поведении компонент девиаторов напряжений и скоростей деформации.

Как вы помните, на рис. 1.4 изображены характерные кривые зависимости напряжения сдвига s₁₂ = t от скорости деформации сдвига для неньютоновских жидкостей при плоском прямолинейном установившемся движении вдоль оси Ох₁. Поведение жидкости, описываемое кривой 3, называется псевдопластичным, а кривой 4 - дилатантным. Различными авторами предлагалось множество аппроксимаций этих кривых, но наиболее широкое применение получили двухпараметрические аппроксимации:

Ø Модель Шведова - Бингама для псевдопластичных жидкостей (вязкопластичная бингамовская жидкость).

(8.1.3)

Характеризуется тем, что обладает пространственной жёсткой структурой и благодаря этому сопротивляется внешнему воздействию до тех пор, пока вызванное им напряжение сдвига не превзойдёт предельного значения, соответствующего этой структуре. После этого структура полностью разрушается и жидкость начинает вести себя как обычная ньютоновская вязкая жидкость при кажущемся напряжении, равном избытку действительного напряжения t над предельным t₀.

Ø Модель Освальда - Вейля (степенная), используемая для обоих типов жидкостей:

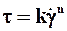, (8.1.4)

где t₀ - предельное (или динамическое) напряжение сдвига; h - пластическая (структурная) вязкость; k - показатель консистенции; n - показатель неньютоновского поведения: при n < 1 жидкость псевдопластичная, при n > 1 - дилатантная.

Между параметрами моделей устанавливается следующая связь:

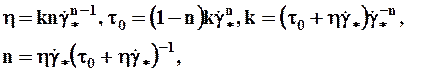
где - скорость деформации сдвига, выше которой зависимость t от 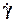практически линейна.

Отметьте тот факт, что реологические параметры h,t₀,k, n - для тампонажного и бурового растворов зависят от температуры, давления, состава, диапазона изменения скорости деформации сдвига , для которой справедливы модели (8.1.3) и (8.1.4).

4. Чтобы установить характер зависимости между касательными напряжениями и скоростями деформации сдвига и определить реологические параметры жидкости в заданных условиях, используют наиболее простые формы движения:

Ø установившееся ламинарное (слоистое) течение жидкости вдоль оси цилиндрической трубы;

Ø тангенциальное течение между двумя соосными цилиндрами.

При этих течениях линии тока либо прямые линии, либо - концентрические окружности. Такие течения можно создать лишь в специальных приборах: капиллярных или ротационных вискозиметрах.

Дата добавления: 2014-12-26