Кинематика вращательного движения материальной точки

Помимо линейных характеристик движения: линейной скорости n и линейных ускорений a_t, a_n при движении материальной точки по окружности вводят угловые характеристики движения: w - угловую скорость, e - угловое ускорение.

1. Угол поворота. Пусть тело повернулось на угол j. Поворот тела можно задать в виде псевдовектора j, длина которого равна углу j, а направление совпадает с осью вращения в сторону, определяемую правилом правого винта. Малые повороты можно рассматривать как псевдовектор dj.

2. Угловая скорость. Мгновенная угловая скорость равна производной по времени от угла поворота j:

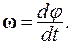(1.15)

Вектор 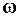направлен вдоль оси вращения материальной точки по правилу правого винта (рис. 1.7).

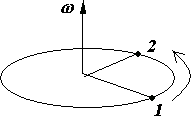
Рис. 1.7.

При равномерном вращении угловая скорость

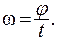(1.16)

Размерность угловой скорости: [w] = рад/с.

3. Угловое ускорение. Мгновенным угловым ускорением называется псевдовектор e, равный первой производной от вектора угловой скорости w:

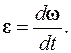(1.17)

Вектор e направлен вдоль оси вращения материальной точки. Размерность углового ускорения: [e] = рад/с.

Поскольку угловая скорость является первой производной от угла поворота (1.15), то угловое ускорение можно записать как вторую производную от угла поворота:

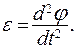(1.18)

4. Период обращения. Время совершения материальной точкой полного оборота называется периодом обращения:

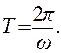(1.19)

Размерность периода обращения: [T] = с. Число оборотов в единицу времени называется частотой:

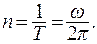(1.20)

Размерность частоты: [n] = 1/с.

5. Уравнения кинематики вращательного движения материальной точки. Запишем угол поворота j и угловую скорость w при неравномерном вращательном движении:

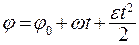(1.21)

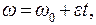
где 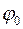- начальный угол;

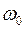- начальная угловая скорость;

e- угловое ускорение.

При равномерном движении e = 0. Уравнения кинематики вращательного движения принимают вид

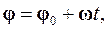
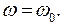(1.22)

6. Связь между характеристиками поступательного и вращательного движения. Линейная скорость n связана с угловой скоростью w соотношением (формула Эйлера)

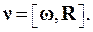(1.23)

Тангенциальное ускорение 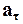связано с угловым ускорением 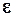формулой

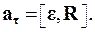(1.24)

Нормальное ускорение 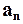связано с угловой скоростью w соотношением

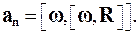(1.25)

Контрольные вопросы:

1. Перемещение, путь.

2. Мгновенная и средняя скорость, средняя путевая скорость.

3. Мгновенное и среднее ускорение.

4. Тангенциальное, нормальное и полное ускорение.

5. Угол поворота, мгновенная угловая скорость и средняя угловая скорость.

6. Уравнения кинематики поступательного и вращательного движений

ГЛАВА 2. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЁРДОГО ТЕЛА

Дата добавления: 2014-12-26