Статистический вес

Рассмотрим систему, состоящую из большого количества молекул. Назовем ее макроскопической системой. Состояние такой системы можно описать двумя способами:

1. С помощью средних характеристик системы, например, давления P, объёма V, температуры T, энергии Е. Состояние, заданное характеристиками, усреднёнными по большому числу молекул, будем называть макросостоянием.

2. Путем описания состояния всех образующих тело молекул, для этого необходимо знать координаты q и импульсы p всех молекул. Состояние, заданное таким образом, назовём микросостоянием.

Пусть макроскопическая система является частью какой – либо большой замкнутой системы, будем называть ее средой. Найдём микроскопическое распределение Гиббса, т.е. функцию распределения вероятностей различных состояний макроскопической системы, не взаимодействующей с окружающими телами и имеющей постоянную энергию. Различные состояния системы, имеющие одну и ту же энергию, имеют одинаковую вероятность.

Каждому значению энергии макроскопической системы могут соответствовать различные микросостояния, число таких состояний называется статистическим весом.

Пусть задано макросостояние системы из 4 молекул с помощью параметров: P, V, T, E. Молекулы находятся в сосуде, разделенном проницаемой перегородкой (рис. 10.1а). Cосуд находится в некоторой среде, но не взаимодействует с ней.

Рис. 10.1а. Рис. 10.1б. Рис. 10.1в.

Если все 4 молекулы находятся в правой половине сосуда, то макросостояние системы (0 - 4) можно записать с помощью одного микросостояния, перечислив номера молекул. В этом случае статистический вес .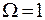

Пусть теперь одна из молекул перешла в левую половину сосуда (рис. 10.1б). Это может быть молекула 1, тогда в правой половине останутся молекулы 2, 3, 4 или это молекула 2, тогда справа останутся молекулы 1, 3, 4 и т.д. Всего возможны 4 различных микросостояния, следовательно, статистический вес макросостояния (1 - 3) .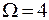

Вероятности всех микросостояний одинаковы. Состояние, когда молекула 1 слева, а 2, 3, 4 справа, имеет такую же вероятность, как состояние, когда молекула 2 слева, а 1, 3, 4 справа. Этот вывод основан на предположении, что все молекулы неотличимы друг от друга.

Равномерное распределение молекул по обеим половинам сосуда становится очевидным при большом количестве молекул. Мы знаем, что давление выравнивается со временем в обеих половинах сосуда: а поскольку концентрация молекул 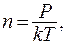то 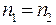и при постоянной температуре одинаковым будет число молекул слева и справа:

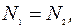
где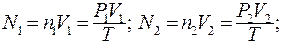

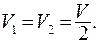
Поскольку наибольшему статистическому весу 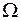соответствует наибольшая вероятность состояния w, то очевидно, вероятность пропорциональна числу состояний. Состояние (2 - 2) является наиболее вероятным, т.к. имеет наибольший статистический вес 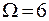(рис. 10.1в).

Дата добавления: 2014-12-26