Распределение Больцмана молекул в потенциальном поле. Барометрическая формула

Если система находится во внешнем поле с потенциальной энергией 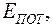то в распределении Гиббса следует учитывать не только различие молекул по скоростям (распределение Максвелла), но и распределение Больцмана молекул по координатам.

Поскольку кинетическая энергия системы не зависит от координат, а потенциальная энергия не зависит от импульсов, то из распределения Гиббса можно выделить распределение Больцмана по координатам:

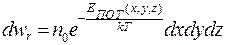(10.12)

где 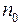- концентрация молекул при = 0.

Концентрация частиц в потенциальном поле зависит от положения их в пространстве:

(10.13)

Потенциальная энергия молекулы с массой m в поле тяжести: 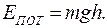Подставим это выражение в распределение Больцмана для концентрации:

(10.14)

На поверхности Земли h = 0 и = 0, следовательно . Чем выше располагаются молекулы от поверхности Земли, тем меньше их концентрация. Основное уравнение молекулярно - кинетической теории позволяет записать давление как функцию температуры и концентрации в виде 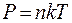. Будем считать атмосферу изотермической, 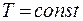. Домножим (10.14) справа и слева на и запишем барометрическую формулу:

(10.15)

где - давление у поверхности Земли;

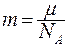- масса молекулы;

m - молярная масса;

- универсальная газовая постоянная.

Барометрическая формула позволяет определить давление атмосферы в зависимости от высоты. С ростом высоты h давление падает быстрее при уменьшении температуры атмосферы (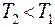) и увеличении молярной массы воздуха .

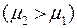Контрольные вопросы:

1. Макро и микросостояния системы. Энтропия в статистической физике.

2. Связь статистического веса с энтропией.

3. Статистический вес и вероятность состояния.

4. Равновесное состояние и равновесный процесс.

5. Обратимый и необратимый процессы.

6. Абсолютная температура и связь ее с энтропией.

7. Распределение Гиббса.

8. Распределение Максвелла молекул по скоростям. Распределение Максвелла по модулям скоростей молекул.

9. Средняя арифметическая и средняя квадратичная скорости молекул.

10. Распределение Больцмана частиц в потенциальном поле. Связь распределений Максвелла и Больцмана с распределением Гиббса.

ГЛАВА 11. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ

Дата добавления: 2014-12-26