Энтропия. Для характеристики вероятности состояния вводят энтропию:

Для характеристики вероятности состояния вводят энтропию:

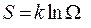(10.1)

где k - постоянная Больцмана.

Пусть 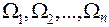статистические веса различных подсистем среды, тогда система будет иметь число микросостояний: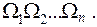

Отсюда находим энтропию замкнутой системы:

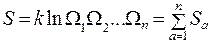
Энтропия сложной системы равна сумме энтропий её частей. В нашем примере мы рассматривали только одну подсистему, статистический вес которой 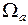зависит от энергии подсистемы 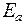. Энтропия также является функцией от энергии:

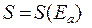
Величина, обратная производной энтропии системы S по её энергии называется абсолютной температурой:

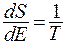(10.2)

отсюда следует

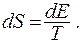(10.3)

Равновесным называется состояние, имеющее наибольший статистический вес. Равновесное состояние не изменяется со временем.

В рассмотренном примере последовательно изучаются равновесные состояния (статистический вес изменяется от 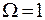до 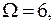образующие стадии равновесного процесса перехода системы в наиболее вероятное из макросостояний. Этот процесс является необратимым, т.к. процесс, обратный ему, является маловероятным. Так, если из одной комнаты газ проник в другую, то невозможно представить, чтобы он через какое - то время опять вернулся в первую комнату.

Вероятность состояния 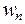системы, находящейся в тепловом контакте со средой, имеющей постоянную температуру T, связана со статистическим весом 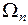соотношением:

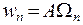
где постоянная нормировки A определяется из условия: 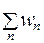(вероятность, что система будет находиться в одном из возможных состояний равна 1).

Статистический вес связан с энтропией данного состояния:

,

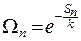а энтропия при Т = const описывается соотношением:

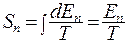. (10.4)

Дата добавления: 2014-12-26