Уравнения движения и равновесия

Основным динамическим уравнением движения материальной точки является 2-й закон Ньютона m` a = `F, а широко используемым следствием этого закона являются следующие общие теоремы движения системы материальных точек:

· производная по времени от количества движения

равна сумме всех действующих на систему внешних сил

(6.7.1)

и называется уравнением количества движения, или уравнением импульсов:

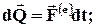
· производная по времени от кинетического момента

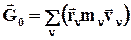
системы относительно какого-либо неподвижного центра О равна сумме моментов

всех внешних сил, действующих на систему, относительно того же центра, т.е.

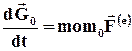, (6.7.2)

называется уравнением моментов количества движения;

· дифференциал кинетической энергии

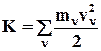
системы равен сумме элементарных работ

всех действующих на систему внешних 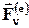и внутренних 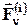сил, т.е.

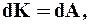(6.7.3)

называется уравнением механической энергии (теоремой живых cил).

· Для любого мысленно выделяемого индивидуального объёма сплошной среды V, ограниченного поверхностью S, уравнения (1.68) - (1.70) действительны, если динамические величины определить следующим образом:

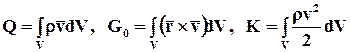
(соответственно количество движения, момент количества движения и кинетическая энергия сплошной среды в объёме V);

(соответственно сумма внешних объёмных и поверхностных сил и их моментов относительно некоторого неподвижного центра О, действующих на среду в объёме V). Силы и их моменты непрерывно определены и сосредоточены.

Сумма элементарных работ внешних и внутренних объёмных и поверхностных сил

.

В этом случае уравнения (6.7.1) и (6.7.2) являются основными постулируемыми динамическими соотношениями механики сплошной среды. Они служат исходными уравнениями для описания любых движений сплошной среды, в том числе разрывных движений и ударных процессов.

Уравнение (6.7.3) одно из наиболее важных следствий уравнений (6.7.1) и (6.7.2) при непрерывных движениях в пространстве и времени.

При непрерывных движениях интегральная теорема движения (6.7.1) эквивалентна следующим 3 дифференциальным уравнениям:

· в декартовой системе координат:

· в цилиндрической системе координат при осевой симметрии

(6.7.4)

где проекции ускорения вычисляют по формулам (1.6).

Эти уравнения, связывающие компоненты v_i вектора скорости и тензора напряжений , являются основной системой дифференциальных уравнений движения для любой сплошной среды, представляющих собой уравнение баланса количества движения (импульса) для бесконечно малого объёма среды. Если движения частиц происходят без ускорения (а_i = 0) или они пренебрежимо малы, то уравнения (6.7.4) называются дифференциальными уравнениями равновесия.

При непрерывном движении сплошной среды теорема моментов количества движения (6.7.2) в дифференциальной форме сводится к выводу о том, что тензор напряжений симметричен, т.е. s_ij = s_ji. Если тензор напряжений симметричен, то уравнения моментов количества движения удовлетворяются тождественно.

Интегральная теорема живых сил (6.7.3) эквивалентна следующему дифференциальному уравнению:

dK = dW = dA^(e), (6.7.5)

где

соответственно изменение кинетической и потенциальной энергии бесконечно малого объёма сплошной среды, элементарная работа внешних объёмных и поверхностных сил, действующих на бесконечно малый элемент объёма среды.

Уравнение (6.7.5) является следствием уравнения движения(6.7.4) и представляет собой уравнение баланса механической энергии.

В общем случае оно не является законом сохранения энергии, но его можно так трактовать тогда, когда механическая энергия тела не переходит в тепловую или другие виды энергии. Общий закон сохранения энергии в этом случае распадается на два:

· закон сохранения механической энергии;

· закон сохранения энергии другого вида.

Дата добавления: 2014-12-26