Основные термины и понятия. Одномерное приближение - весьма эффективный способ описания движения жидкости в случае, если продольные (измеренные вдоль на­правления движения) размеры

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РЕШЕНИЯ ОДНОМЕРНЫХ ЗАДАЧ

Одномерное приближение - весьма эффективный способ описания движения жидкости в случае, если продольные (измеренные вдоль на­правления движения) размеры потока во много раз превосходят его по­перечные размеры, что характерно главным образом для движения жид­кости в трубах, реках и каналах.

Важной особенностью потоков в трубах и каналах является то, что неподвижные твердые границы (стенки трубопроводов, дно рек и кана­лов) составляют значительную часть поверхности, ограничивающей по­ток. На этих границах выполняется условие прилипания, т.е. на них ско­рость жидкости u_гр = 0 (равны нулю и нормальная к границе и касатель­ная к ней составляющие). Благодаря этому на тех границах контрольного объема V, которые совпадают с твердыми границами потока, поверхнос­тные интегралы, входящие в фундаментальные законы гидромеханики и содержащие скорость u или ее проекции, обращаются в ноль. Это существенно упрощает получение расчетных зависимостей, основан­ных на фундаментальных законах.

В достаточно длинных цилиндрических или призматических трубах и каналах формируются потоки жидкости с линиями тока, параллельными твердым границам, в которые заключен поток. Движение жидкости, при котором линии тока представляют собой параллельные прямые, будем на­зывать равномерным, или параллельно-струйным.

Поперечное сечение потока, ортогональное линиям тока, называют живым сечением. При равномерном движении жидкости живое сечение плоское. Благодаря этому, в частности, исключается необходимость ис­следовать поле скорости и появляется возможность оперировать сред­ним по сечению значением скорости.

Это связано с тем, что вектор скорости u (как и линия тока) перпен­дикулярен к живому сечению и проекция скорости на нормаль к этому сечению u_n равна модулю скорости:

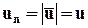. (7.1.1)

Кроме того, при равномерном дви­жении справедливы два следующих утверждения (леммы}:

1. Нормальное напряжение р_nn в каждой точке живого сечения равно
гидродинамическому давлению р в этой точке со знаком минус (так как
положительным считается растягивающее нормальное напряжение):

. (7.1.2)

2. Гидродинамическое давление р в живом сечении распределено по
гидростатическому закону

pU - p = const, (7.1.3.)

где U - потенциал внешней массовой силы; р - плотность жидкости.

При неравномерном движении жидкости, когда линии тока непарал­лельны и (или) криволинейны, различают:

· плавноизменяющееся движение, при котором можно пренебречь кри­визной линий тока и их непараллельностью и с достаточной для практических целей точностью построить плоское живое се­чение, допуская, что в нем выполняются условия (7.1.1), (7.1.2) и (7.1.3);

· резкоизменяющееся движение, при котором нельзя использовать ука­занные условия.

Рис.7.1. Равномерное, плавноизменяющееся и резкоизменяющееся движение жидкости

Для иллюстрации рассмотрим течение в трубопроводе, представ­ленное на рис. 7.1.

На длинных цилиндрических участках I и VII движение равномер­ное, линии тока параллельны обра­зующим стенок трубы.

На криволинейном участке III движение резкоизменяющееся, здесь хотя и можно построить плоские живые сечения, но в них не будут выполняться условия (7.1.2) и (7.1.3).В частности, вследствие действия центробежных сил, обусловленных кривизной линий тока, давление в плоских живых сечениях не будет распределено по гидростатическому закону (7.1.3).

На участке V движение резкоизменяющееся; здесь живое сечение (ортогональное линиям тока) сильно искривлено, так что даже вычисле­ние его площади является непростой задачей, кроме того, вследствие зна­чительной кривизны линий тока в этих сечениях не выполняются условия (7.1.2) и (7.1.3).

На участках II, IV и VI движение неравномерное, но в пределах этих участков можно с достаточной точностью и построить плоское живое сечение, и допустить выполнение равенств (7.1.2) и (7.1.3).

Задачи механики жидкости и газа, основанные на использовании при­веденных выше понятий (плоское живое сечение, равномерное и плавно-изменяющееся движение и др.), называются одномерными.

В технической механике жидкости (гидравлике) потоки разделяют на на­порные, безнапорные и струйные. Если поток со всех сторон ограничен твер­дыми стенками, то он называется напорным (например, поток воды в водопро­водных трубах). Если только часть потока ограничена твердыми стенками, а на остальной части жидкость граничит с газом (в частности, с атмосферой), т.е. ограничена свободной поверхностью, то такое движение называется безна­порным (например, потоки в реках, каналах). Если же поток не ограничен твердой поверхностью, то он называется струйным, или просто струей. Струя жидкости может быть ограничена той же самой жидкостью (затопленная струя) или газом (струя воды в воздухе).

Дата добавления: 2014-12-26