Уравнение Бернулли для установившегося напорного потока вязкой жидкости

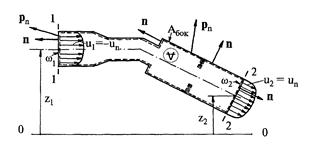Рис. 7.2. Контрольный объём для вывода уравнения Бернулли

Уравнение Бернулли для установившегося потока вязкой жидкости является выражением закона изменения кинетической энергии приме­нительно к одномерным задачам гидромеханики. Выделим в трубопрово­де (рис. 7.2) сечениями 1-1 и 2-2, в которых движение равномерное или плавноизменяющееся контрольный объем V, ограниченный контрольной поверхностью А, показанной штриховой линией. Запишем для выделен­ного объема V закон изменения кинетической энергии:

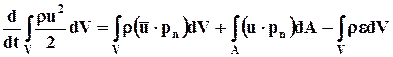. (7.2.1)

Преобразуем слагаемые, входящие в это уравнение, представляя объем­ные интегралы в виде поверхностных и используя условия на контрольной поверхности А, которую запишем в виде сум­мы А = w₁ + w₂ +А_бок.

1. В субстанциальной производной

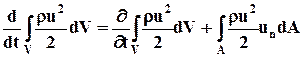(7.2.2)

первое слагаемое равно нулю, так как движение жидкости установивше­еся, и жидкость несжимаема (r= const), а второе слагаемое представляет собой поток кинетической энергии Q_k через контрольную поверхность А. Условия на контрольной поверхности А имеют вид (рис. 7.2)

(7.2.3)

Преобразуем второе слагаемое в (7.2.2), используя (7.2.3), (5.11) и (5.27):

(7.2.4)

2. Обратимся в уравнении (7.2.1) к слагаемому, выражающему мощность внешней массовой силы. Предположим, что внешняя массовая сила имеет потенциал, т.е. существует такая скалярная функция U, для кото­рой f = gradU. Используя теорему Остроградского - Гаусса и граничные условия (7.2.3), получаем

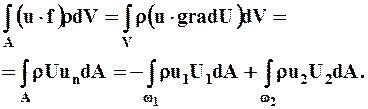(7.2.5)

Полученное равенство позволяет выразить мощность внешней мас­совой силы через поток потенциальной энергии, обусловленной этой силой, сквозь живые сечения.

3. Рассмотрим интеграл, выражающий мощность внешней поверхно­стной силы:

. (7.2.6)

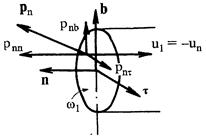Рис.7.3. Напряжение и скорость жидкости в поперечном сечении w₁

В сечении 1 - 1 скорость имеет только нормальную составляющую u_n, так как движение здесь равномерное или плавноизменяющееся. Чтобы вы­числить скалярное произведение u • р_n, зададим в произвольной точке живого сечения w₁ систему ортогональных координат (рис. 7.3), определяе­мую тремя единичными векторами (n, b, t), из которых n - нормален к живому сечению, a b и t лежат в его плоскости. Проектируя на эти коор­динатные оси векторы u и р_n, находим

u = (u_n, u_b,u_t) = (u_n, 0, 0); р_n = (p_nn, p_nb, р_пt),

при этом все три проекции напряжения р_n могут быть отличны от нуля. По определению скалярного произведения

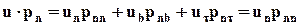. (7.2.7)

Аналогичные вычисления выполним для живого сечения w₂. На поверхности А_бок выполняется условие прилипания. Согласно полученным результатам, а также используя (7.1.2), на контрольной поверхности А имеем условия:

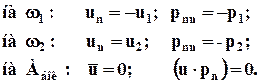(7.2.8)

Подставляя (7.2.8) в (7.2.7) и в (7.2.6), получаем

. (7.2.9)

Согласно равенству (7.2.9) мощность внешней поверхностной силы можно интерпретировать как поток, обусловленный этой силой потен­циальной энергии сквозь живое сечение; в соответствии с (3.13) плот­ность распределения этой энергии равна давлению р.

Сложим равенства (7.2.5) и (7.2.6) и найдем выражение для мощности внешних сил, которое в соответствии с вышеизложенным будем интер­претировать как поток потенциальной энергии Q_p, обусловленный внеш­ними массовой и поверхностной силами через контрольную поверхность:

.

Примем во внимание, что в сечениях 1 - 1 и 2 - 2 движение равно­мерное или плавноизменяющееся, и, следовательно, согласно (7.1.3) дав­ление в этих сечениях распределено по гидростатическому закону: rU - р = const.

В соответствии с этим выражение в скобках в интегралах по живым сечениям можно вынести за знак интеграла. Кроме того, положим, что сила тяжести является единственной внешней массовой силой, т.е., что U = - g z. В результате получим

^. (7.2.10)

4. Последнее слагаемое в (7.2.1), выражающее мощность внутренних сил в пределах контрольного объема, оставляем без преобразования.

Подставив (7.2.4) и (7.2.10) в исходное уравнение (7.2.1) и разделив все слагаемые на весовой расход Q_B = rgQ, получим искомое уравнение Бернулли:

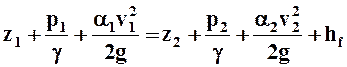, (7.2.11)

где g = rgQ удельный вес, а слагаемое

(7.2.12)

выражает отнесенную к весовому расходу мощность внутренних сил (дис­сипацию механической энергии в единицу времени) в пределах конт­рольного объема.

Для сжимаемой жидкости (газа) можно выполнить аналогичный вы­вод и получить уравнение Бернулли в виде

, (7.2.13)

где r₁ и r₂ - плотности жидкости (газа) в сечениях 1 - 1 и 2 - 2.

Дата добавления: 2014-12-26