Формулы фильтрации

Закон Дарси. При очень медленном движении жидкости в пористой среде (пласте), когда силы инерции ничтожно малы и ими можно пренебречь, для скорости фильтрации принят так называемый линейный закон фильтрации, или закон Дарси:

, (9.3.1)

где DH/ l - потеря напора на единицу длины пласта (соответствует гидравлическому уклону i).

Коэффициент пропорциональности К в формуле (2.36) называется коэффициентом фильтрации. Он характеризует одновременно фильтрационную способность среды и протекающей в нём жидкости. [К] = [см/с].

Закон Дарси можно выразить через коэффициент проницаемости k, характеризующий пористую среду, и динамический коэффициент вязкости m жидкости:

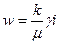, (9.3.2)

g - удельный вес жидкости.

Расход жидкости Q, протекающий через площадь фильтрации f, определяется формулой:

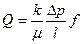. (9.3.3)

Закон Дарси в дифференциальной форме

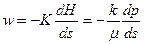, (9.3.4)

где s - направление, которое берётся вдоль струйки по скорости v.

Для коэффициента проницаемости имеем

(9.3.5)

[k] = см².

1 дарси = .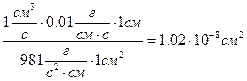

Коэффициент проницаемости равен 1 дарси при абсолютной вязкости m = 1 сантипуазу, Dр =1 ат на длине 1 см, площади сечения 1 см² и расходе жидкости 1 см³/с.

При движении жидкости в крупнозернистых грунтах закон ламинарной фильтрации нарушается в связи с турбулентным характером течения. Такое нарушение может происходить и при ламинарном движении за счёт сравнительно высоких скоростей течения, при которых нельзя пренебрегать влиянием сил инерции.

Критерием существования ламинарной фильтрации является число Рейнольдса.

· По Н.Н. Павловскому .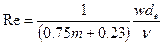

При этом 7< Re_кр < 9.

· По В.Н. Щелкачёву , 1< Re_кр < 12.

· М.Д. Миллионщиков ввёл в формулу Рейнольдса внутренний масштаб породы (линейный размер ) l^*:

,

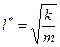где k - коэффициент проницаемости, m - пористость; за характерную скорость принимается истинная скорость фильтрации, равная .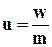

Тогда

. (9.3.6)

Критическое значение 0.022 < Re_кр< 0.290.

Если фильтрация не подчиняется закону Дарси (нелинейна), то используют следующие представления:

· скорость w или дебит Q представляются степенной зависимостью от градиента давления

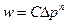, (9.3.7)

где C и n некоторые коэффициенты;

· двучленной формулой для градиента давления вида

, (9.3.8)

где - dS - элемент струйки, b - коэффициент, зависящий от геометрии пористой среды, шероховатости и т.п.

Скорости фильтрации струек пропорциональны расходам (дебитам), поэтому двучленный закон сопротивления при нелинейной фильтрации может быть представлен уравнением индикаторной кривой для несжимаемой жидкости в виде

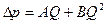, (9.3.9)

графически изображаемой параболой.

Для газа (воздуха) будем иметь

,

где А₁ и В₁ - параметры, характерные для данного пласта и скважины.

Ø Л.С. Лейбензон, исходя из общей теории фильтрации, предложил определять скорость фильтрации по формуле:

;

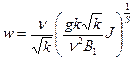здесь n - кинематический коэффициент вязкости, J - гидравлический уклон, k - проницаемость, B₁ - постоянная величина. При квадратичной турбулентной фильтрации показатель степени S = 2.

Движение газа в пористой среде. Общее уравнение установившегося движения газа через пористую среду имеет вид

, (9.3.10)

где q - функция давления,

Уравнения движения газов в пористой среде нелинейны и решить их можно только в некоторых конкретных случаях при введении определённых упрощений.

Рассмотрим несколько частных решений, представляющих интерес с позиций проводки нефтяных и газовых скважин и широко используемых в различных расчётах при бурении.

Пусть при бурении скважины радиусом r_с частично (рис. 9.1,б) или полностью (в) вскрыт проницаемый пласт кругового контура радиусом R_k, имеющий непроницаемые кровлю, подошву и толщину h (рис.9.1).

Рис.9.1.Схемы вскрытия проницаемого пласта скважиной

В случае применимости закона Дарси для несжимаемой жидкости справедливы следующие формулы для расчёта расхода при стационарной фильтрации.

При большой мощности пласта (рис.9.1,а) имеем формулу для расчёта расхода на стенках скважины:

, или , т.к. 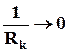. (9.3.11)

При этом для р_k > р_с скважина проявляет с дебитом Q, а в противном случае поглощает.

При условии r_с << h и незначительном заглублении (рис.9.1, б) формула для расчёта с удовлетворительной для инженерных расчётов точностью имеет вид

(9.3.12)

Аналогично при р_k > р_с имеет место проявление с дебитом Q, а в противном случае поглощение.

Наконец, (рис.9.1, в) расход определяется по формуле Дюпюи:

(9.3.13)

при тех же условиях.

Во всех приведённых формулах индексы «с» и «k» означают скважину и контур, а под давлением р_k понимается пластовое давление.

Обычно крайне трудно задаваться радиусом контура R_k. Если при его задании ошибиться в m раз, то

При условии, что R_k обычно в сотни или тысячи раз больше h или r_с, первые члены будут на порядок больше вторых членов при m = 2÷3. Поэтому погрешности от ошибочного задания радиуса контура в 2-3 раза приводят к ошибкам порядка 10%. Т.е. двух и трёхкратные ошибки при задании R_k вполне допустимы.

Приведённые выше формулы применены при фильтрации по закону Дарси, а во многих случаях вскрываются трещинные и порово-трещинные коллекторы, для которых справедливы законы течения, описываемые формулами Форхгеймера или Краснопольского - Шези. В случае применимости закона Краснопольского - Шези формула для расчёта расхода имеет вид

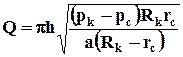, (9.3.14)

где а - постоянная характеристика фильтрации.

Принимая во внимание, что r_k >> r_с, последнюю формулу можно записать в виде

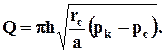(9.3.15)

При фильтрации по закону Форхгеймера расчётная формула для определения Q приближённо записывается в виде

(9.3.16)

где b - постоянная двухчленного закона фильтрации.

Все приведённые выше формулы могут использоваться и для течения газов. В этом случае вместо разности давлений необходимо применять разность квадратов давлений, т.е. а вместо объёмного расхода Q определяется приведённый к стандартным условиям (например, к пластовой температуре и атмосферному давлению) объёмный расход Q_прив. Так, формула Дюпюи при течении газов имеет вид

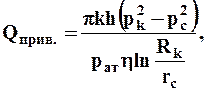(9.3.17)

а для случая одномерного течения соответствующая формула была приведена выше, где в отличие от формулы для жидкости появился множитель (где р_ат - атмосферное давление).

Дата добавления: 2014-12-26