Ламинарное и турбулентное течение жидкостей в щелевом канале

1. Ламинарное течение ньютоновской жидкости. Согласно соотношениям Коши и уравнениям состояния при течении жидкости в щели, отличными от 0 будут лишь одна скорость деформации и одно напряжение сдвига (10.1.1):

Из уравнений состояния сохранится лишь одно, а именно

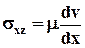. (10.2.1)

Сравнивая это уравнение с решением (10.1.3)

,

получаем дифференциальное уравнение относительно скорости

,

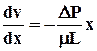решение которого при граничном условии v(h) = 0, (2h - ширина щели) имеет вид

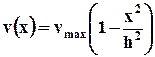. (10.2.2)

Используя формулы (10.1.4), можно определять основные характеристики потока:

· объёмный расход

· среднюю скорость

· коэффициент сопротивления

,

где

· S, S_d - соответственно площади поперечного сечения и боковой смоченной поверхности канала;

· f = t / W - коэффициент трения Фаннинга;

· - касательное напряжение у поверхности канала; 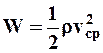- кинетическая энергия единицы объёма жидкости;

· b - длина поперечного сечения щели;

· - параметр Рейнольдса для плоской щели.

Например: при r = 1000кг/м³; v_ср = 1 м/с; 2h = 0,01 м; m = 0,01Па×с;

имеем: Re_щ = 1000; l = 0,048; DP/L = 1200 Па/м. Таким образом, на каждые 1000 м гидравлические потери составят 1.2 МПа.

2. Ламинарное течение неньютоновской жидкости Шведова - Бингама. Используя соотношение (5.1) и подставляя его в (1.87) - интенсивность касательных напряжений и (1.88) - интенсивность скорости деформации сдвига при скорости деформации объёма (x = 0), будем иметь:

. (10.2.3)

Знак (-) выбран из-за того, что .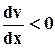

Система уравнений упрощается до одного уравнения

(10.2.4)

Сравнивая (10.2.4) с (10.1.3), получаем уравнение скорости

(10.2.5)

и формулу для вычисления ядра потока

. (10.2.6)

Интегрируя уравнение (10.2.5) при v (h) = 0, найдём следующее распределение скорости:

(10.2.7)

Отсюда следует:

Ø при h₀ = h движение жидкости происходить не будет, т.к. v (x) = 0;

Ø условием существования движения является h₀ < h или, используя формулу (10.2.6),

Если учесть, что начало движения рассматриваемой жидкости обусловлено не динамическим напряжением сдвига t₀, а статическим t₀₀ > t₀, то условием страгивания покоящейся жидкости будет

.

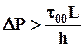По формулам (10.1.4) определяют основные характеристики потока (впервые получены М.П. Воларовичем и А.М. Гуткиным):

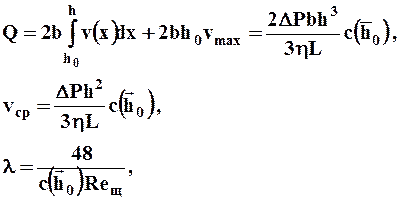(10.2.8)

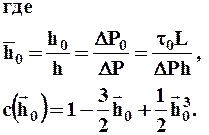
Как видно из полученных выражений, кинематические характеристики потока Q, v_ср и коэффициент сопротивления l зависят от градиента давления нелинейно, что вызывает трудности при решении обратной задачи.

Если исходить из того, что практический интерес представляет случай, когда DР >>DR₀ (`h<sub>0</sub><<1), то, приняв c (`h₀) = 1- 3/2`h₀, получим:

(10.2.9)

где - обобщённый параметр Рейнольдса; h_* = h (1+ 1/4Sen_щ) - приведённая вязкость жидкости Шведова - Бингама; Sen_щ = t₀2h/hv_ср - параметр Сен-Венана для плоской щели.

Например, при r = 1350 кг/м³, t₀ = 5 Па, h = 0.04 Па ×с; v_ср = 1 м/с, h = 0.02 м. Получим:

т.е. в этом случае на каждые 1000 м гидравлические потери составляют 0.675 МПа.

2. Неньютоновская жидкость Освальда - Вейля. Используя в системе уравнений Коши соотношения (10.1.1) и (10.2.3)

и

,

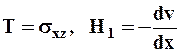получим .

Сопоставляя это уравнение состояния с решением (5.3), приходим

к дифференциальному уравнению относительно скорости:

. (10.2.10)

Интегрируя это уравнение при граничном условии v (h) = 0, получаем распределение скорости:

, (10.2.11)

где .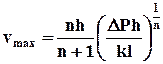

Интегральные характеристики потока при этом будут

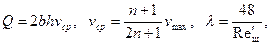(10.2.12)

где 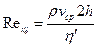- обобщённый параметр Рейнольдса,

- приведённая вязкость жидкости Освальда -Вейля для плоской щели.

При n = 1 и k = m формулы (10.2.11) - (10.2.12) совпадут с формулами (10.2.3) - (10.2.4).

3. Турбулентный режим течения. Когда параметры Re, Re^* или Re^’ больше критических значений, решение уравнения движения записывается в виде (сравните с (10.1.3)

.

Касательное напряжение s_ij в зависимости от типа жидкости связано со скоростью сдвига уравнениями вида (10.2.1), (10.2.3) или (10.2.10). Напряжение Рейнольдса в силу соотношений (10.2.3) удовлетворяет уравнению Прандтля:

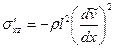, (10.2.13)

где принимается, что величина l линейно зависит от расстояния до стенки канала s = h - х, т.е.

ℓ = æS (10.2.14)

где æ - константа, определяемая из опыта.

Напряжение s_ij имеет существенное значение лишь в непосредственной близости от стенок канала, т.е. в узкой области, состоящей из ламинарного подслоя и буферной зоны, где ламинарные и турбулентные законы течения сравнимы между собой.

В основной области течения (турбулентное ядро) можно пренебречь напряжением. Поэтому после подстановки (5.17) и (5.18) в (5.16) получим следующее исходное дифференциальное уравнение:

при s ³ s₁, (10.2.15)

где t_* = DRh/L – приведённое значение касательного напряжения; s₁ – внешняя граница буферной зоны.

Упрощение t_* введено Прандтлем без какого-либо физического обоснования, но большой погрешности в решение не вносит. Если, кроме того, ввести обозначение для динамической скорости на стенке канала , то уравнение (10.2.15) примет вид

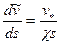при s ³ s₁.

Интегрируя это уравнение при условии 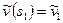, получаем универсальный закон распределения скорости:

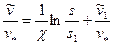при s ³ s₁. (10.2.16)

Многочисленные экспериментальные подтверждения показали, что логарифмическое распределение (10.2.16) достаточно хорошо описывает профили скорости при турбулентных течениях различных жидкостей в плоских и круглых каналах с гладкими и шероховатыми стенками вплоть до больших значений параметра Рейнольдса (за исключением узких пристенных областей). Различия могут составлять лишь входящие параметры.

Дата добавления: 2014-12-26