Ламинарное и турбулентное течение жидкостей в кольцевом канале

1. Для ньютоновской жидкости, используя соотношение для скорости деформации и напряжения сдвига (10.1.1) в системе уравнений (1.85), получаем простейшее уравнение состояния .

Сравнивая с решением (10.1.4), получаем для скорости:

.

Решая это дифференциальное уравнение при граничных условиях v(aR) = v(R) = 0, получаем:

, (10.3.1)

где aR и R (0 £ a £ 1) - радиусы внутреннего и внешнего цилиндров, ограничивающих кольцевой канал.

, . (10.3.2)

Скорость жидкости будет максимальной при , а максимальные характеристики потока при этом будут:

(10.3.3)

где

Re_кр - параметр Рейнольдса для кольцевого канала.

При a > 0.3 j» 1.5 и поэтому l» 96/Re_кр.

Кольцевой цилиндрический канал с соотношением радиусов окружностей сечения a > 0.3 и плоская щель с параметрами сечения 2h = R(1-a) b = pR(1+a) эквивалентны по интегральным гидродинамическим характеристикам при ламинарном течении ньютоновской жидкости (средняя скорость, расход, коэффициент трения, перепад давления). Переход от ламинарного режима течения к турбулентному в кольцевом пространстве наступает быстрее, чем в плоской щели, так как . При a = 0 (w = 0, j = 0) из формул (5.21) - (5.23) получаются известные формулы Гагена - Пуазейля, характеризующие течение жидкости в круглой трубе:

где - параметр Рейнольдса для трубы.

2. Для ньютоновской жидкости Шведова - Бингама течение в кольцевом канале возможно лишь при соблюдении условия

.

Аналитического решения этой задачи нет, возможно только численное. В результате сравнения с решением для кольцевого цилиндрического канала делается полезный вывод о том, что при течении жидкости Шведова - Бингама имеет место гидравлическая эквивалентность кольцевого цилиндрического канала и плоской щели, если DР>2DP₀: a > 0.3; 2h=R(1-a); b = pR(1- a); t¢₀/t₀ =4/3j₁ = 1.16 ¸ 1.17, где t¢₀ и t₀ - соответственно предельные напряжения сдвига для жидкостей в щелевом и кольцевом каналах.

Если принять j₁ = ¾, т.е. h_* = h(1 + 1/8 Sen), то последнее требование опускается. Аналогично первой задаче требование .

3. Для неньютоновской жидкости Освальда - Вейля задача решена только численно.

В предельном случае, когда R ® 0 (a = 0, w = 0, R₂ = R), для распределения скорости в сечении круглой трубы имеем

,

где .

При этом основные интегральные характеристики потока жидкости в трубе принимают вид

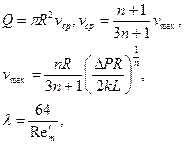
где - обобщённый параметр Рейнольдса,

- приведённая вязкость жидкости для трубы.

4. При турбулентном режиме течения закон сопротивления слабо зависит от формы канала (круглая труба, кольцевое пространство, щель). В диапазоне чисел Рейнольдса 2 10³ < Re _k £ 10⁵ коэффициент сопротивления рассчитывается по формуле Блазиуса .

СПИСОК ЛИТЕРАТУРЫ

1. Гиргидов А.Д. Механика жидкости и газа (гидравлика).- Санкт-Петербург.: Издательство СПбГПУ, 2002. - 544с.

2. Рабинович Н.Р. Инженерные задачи механики сплошной среды в бурении. - М.: Недра, 1989. - 270 с.

3. Ершов Л.В., Максимов В.А. Математические основы физики горных пород. - М.: МГИ, 1968. - 254 с.

4. Тёркот Д., Шуберт Дж. Геодинамика. Геологические приложения физики сплошных сред. – М.: Мир, 1985. – 375 с.

5. Кутепов А.М., Полянин А.Д., Запрянов З.Д., Вязьмин А.В., Казенин Д.А. Химическая гидродинамика. Справочное пособие. - М.: «Бюро Квантум», 1996. - 336 с.

6. Седов Л.И. Механика сплошной среды. – М.: Наука, Главная редакция физико-математической литературы, 1970, Т.1. – 492 с.

7. Седов Л.И. Механика сплошной среды. – М.: Наука, Главная редакция физико-математической литературы, 1970, Т.2. – 568с.

Дата добавления: 2014-12-26