Интерполяционная формула Ньютона №2

Первая интерполяционная формула Ньютона практически неудобна для интерполирования вблизи конца таблицы. В этом случае обычно применяется вторая интерполяционная формула Ньютона.

Пусть имеем систему значений функции 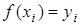для равноотстоящих значений аргумента 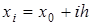, где 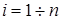. Построим интерполирующий полином следующего вида:

,

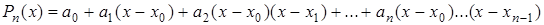где 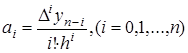. Подставляя эти значения в формулу и полагая 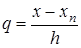получим:

- второй многочлен Ньютона.

Остаточный член 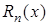второй интерполирующей формулы Ньютона имеет вид:

,

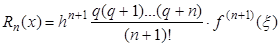где 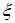- некоторая внутренняя точка наименьшего промежутка, содержащего все узлы 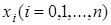и точку .

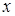Для неограниченной таблицы значений функции y число n в интерполяционной формуле может быть любым, поэтому практически его выбирают так, что бы разность 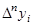была постоянной с заданной степенью точности. В этом случае остаточный член удобней вычислять по формуле:

.

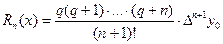Если таблица значений функции конечна, то число n не может быть больше числа значений функции минус единица.

Пример 5.2. Найти приближенное значение функции при данном значении аргумента с помощью первого или второго интерполяционного многочлена Ньютона. Вычислить остаточный член.

Дана таблица значений функции y_i с постоянным шагом 0,005

x	y
1.215	0.106044
1.220	0.106491
1.225	0.106935
1.230	0.107377
1.235	0.107818
1.240	0.108257
1.245	0.108696
1.250	0.109134
1.255	0.109571
1.260	0.110008

Требуется определить значения функции y(x) при следующих значениях аргумента

x ₁= 1.2173; x ₂ = 1.253; x ₃= 1.210; x ₄= 1.270.

Составим таблицу конечных разностей.

i	xi	yi	Dyi	D2yi	D3yi
	1.215	0.106044	0.000447	-0.000003	0,000001
	1.220	0.106491	0.000444	-0.000002	0,000001
	1.225	0.106935	0.000442	-0.000001	-0,000001
	1.230	0.107377	0.000441	-0.000002	0,000002
	1.235	0.107818	0.000439		-0,000001
	1.240	0.108257	0.000439	-0.000001
	1.245	0.108696	0.000438	-0.000001	0,000001
	1.250	0.109134	0.000437
	1.255	0.109571	0.000437	-
	1.260	0.110008	-	-

При вычислении разностей ограничиваемся разностями второго порядка, так как они практически постоянны. При х = 1.2173 и х = 1.210 пользуемся формулой Ньютона №1:

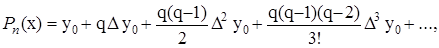
где q = (x-x0)/h.

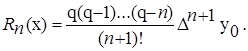
Если x = 1.2173, то q = (1.2173-1.215)/0.005= 0.46;

P1 (1.2173)=0.106044+0.46·0.000447=0.106044+0.0002056=0.106250

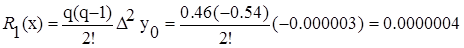
Если x = 1.210, то q = (1.210-1.215)/0.005= -1;

P 1(1.210)= 0.106044+(-1)·0.000447=0.105597

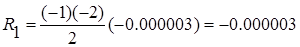
P 2(1.210)= P 1(1.210)+ R 1=0.105600

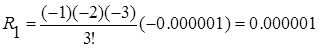
При x = 1.253 и x = 1.270 пользуемся второй формулой Ньютона:

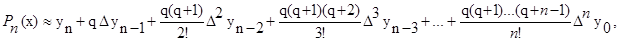
где q = (x-xn)/h.

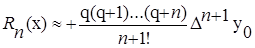
Если x = 1.253, то q = (1.253 - 1.250)/0.005 = 0.6;

P1 (1.253)=0.109134+0.6·0.000438=0.109134+0.000263=0.1093968

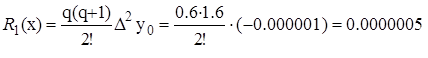
Если x = 1.270, то q = (1.270 - 1.260)/0.005 = 2;

P₁ (1.270)=0.110008+2·0.000437=0.110008+0.000874=0.110882

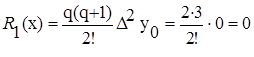
Ответ: f (1.2173)» 0.106250; f (1.253) ·» 0.109397; f (1.210)» 0.105597;

f (1.270)» 0.110882.

Дата добавления: 2014-12-26