Конечные разности. Постановка задачи интерполирования

Постановка задачи интерполирования

Пусть функция 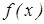задана на отрезке 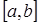в точках , 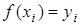i=0,1,2..n, 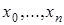называются узлами интерполяции.

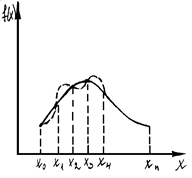
Рис 5.1. Постановка задачи интерполирования

Требуется провести интерполирующую функцию 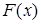определенного класса, проходящую через точки: 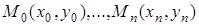, в узлах интерполяции 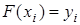i=1,2..n.

Пусть F(x)- это многочлен степени не выше n. Обозначим F(x) через P_n(x), тогда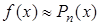

В такой постановке задача имеет единственное решение. Полученную формулу y= P_n(x) используют для вычисления приближенного значения функции f(x) для значений аргумента x, отличных от узлов интерполяции. Эта операция называется интерполирование.

Если 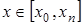, то интерполирование будет в узком смысле, а если 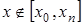то интерполирование в широком смысле (экстраполирование).

Пусть дана функция 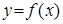и фиксированная величина приращения аргумента 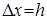. Конечной разностью первого порядка функции y называется выражение. 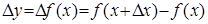Конечной разностью второго порядка называется: 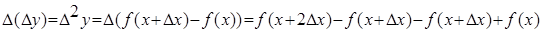. Kонечной разностью n -го порядка называется 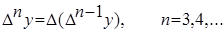. Конечные разности обладают следующими свойствами:

1. ;

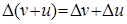2. ;

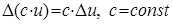3. .

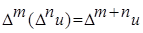Для малых h можно приближенно заменять производные через конечные разности: , ().

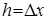Часто приходится рассматривать функции у=f(x), заданные табличными значениями yi=f(xi), для системы равноотстоящих точек xi (i=0,1,2,…), где

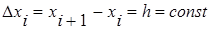. Конечные разности последовательности yi определяются соотношениями

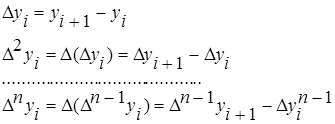
Пример 5.1 Построить конечные разности для функции 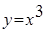с шагом .

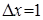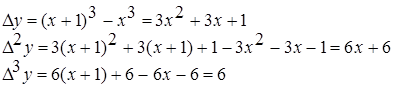
Конечные разности различных порядков удобно располагать в форме таблиц двух видов: горизонтальной (таблица 5.1) или диагональной (таблица 5.2)

Таблица 5.1.

Горизонтальная таблица разностей

….	…	…	…	…	…

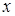
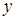
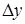
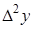
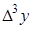
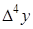
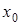
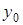
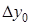
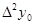
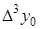
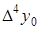
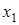
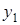
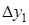
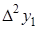
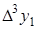
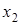
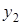
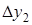
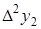
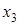
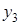
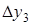
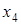
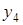
Таблица 5.2.

Диагональная таблица конечных разностей

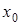
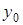
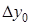
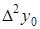
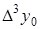
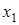
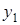
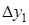
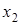
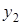
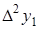
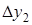
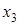
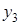
Дата добавления: 2014-12-26