Метод Ньютона для систем нелинейных уравнений

Пусть дана система

Согласно методу Ньютона последовательные приближения вычисляются по формулам

,

,

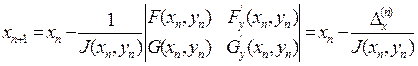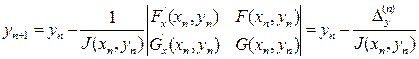где , ,

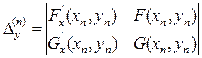а якобиан

.

Начальные приближения и 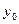определяются приближенно (графически и т.п.).

Метод Ньютона эффективен только при достаточной близости начального приближения к решению системы.

Пример 4.1 Решить нелинейную систему уравнений в Mathcad с пятью верными знаками после запятой.

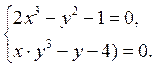
Преобразуем систему, выразив х из обоих уравнений.

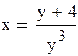
Левые части уравнений исходной системы зададим в виде функций пользователя с двумя переменными.

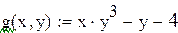
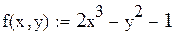
Правые части преобразованной системы зададим в виде функций пользователя от переменной y. Построим их на графике.

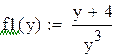
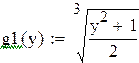
  Точка пересечения кривых на графике лежит в прямоугольнике 1.5<x<1.75;1.1<y<1.3. За начальное приближение корней системы примем x=1.7 и y=1.3

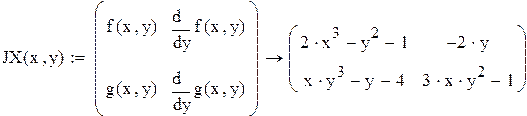
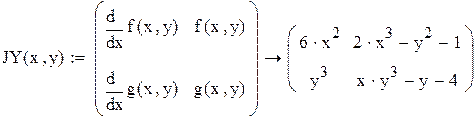
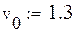
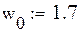
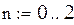
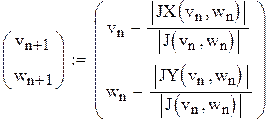
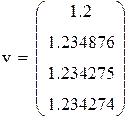
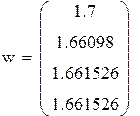
Вычисления с помощью встроенных функций Mathcadа

Ответ: x=1.23427 y=1.66153

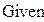
Ответ: x=1.23427 y=1.66153

Рис.4.1. Решение примера 4.1 в Mathcad

4.2. Распространение метода Ньютона на системы из n уравнений с n неизвестными

Рассмотрим нелинейную систему уравнений

(4.1)

с действительными левыми частями.

Можно записать систему в более компактном виде:

,

где , а .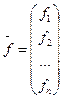

Для решения системы будем пользоваться методом последовательных приближений.

Предположим, что найдено приближение на шаге p

,

где 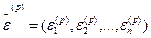- поправки (погрешность корня).

Введем в рассмотрение матрицу Якоби системы функций 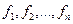относительно переменных :

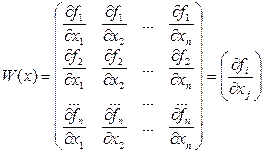
Если эта матрица неособенная, т.е. 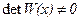, то поправка 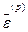выражается следующим образом:

,

где 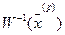- матрица, обратная матрице Якоби.

Таким образом, последовательные приближения находятся по формуле:

.

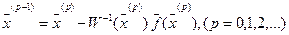За нулевое приближение можно взять приближенное значение искомого корня.

Пример 4.2 Решить систему из примера 4.1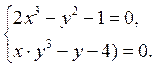

в Mathcad в векторной форме.

Левые части системы зададим векторной функцией

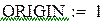
J(x,y) это якобиан системы

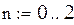
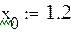
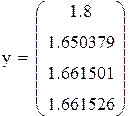
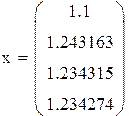
Ответ: x=1.23427 y=1.66153

Рис.4.2. Решение примера 4.2 в Mathcad

Дата добавления: 2014-12-26