Определение подвижности механизмов

Для определения подвижности плоских механизмов следует пользоваться формулой Чебышева:

W = 3n – 2p₅ – p₄,

где W - степень свободы механизма;

n - число подвижных звеньев;

p₁ - число низших кинематических пар (5 класса);

p₂ - число высших кинематических пар (4 класса).

Раздел 2. Кинематический анализ плоских механизмов с низшими парами

Кинематический анализ Механизмов имеет своей целью изучение теории строения механизмов, исследование движения звеньев с геомет­рической точки зрения, независимо от сил, вызывающих движение этих тел.

Кинематическое исследование состоит в решении следующих за­дач:

1. Определение класса механизма, т. е. выяснение, из каких структурных групп состоит механизм, и в какой последовательности эти группы присоединяются к исходному механизму 1 класса.

2. Определение перемещений звеньев и траекторий, описываемых точками звеньев.

3. Определение скоростей отдельных точек звеньев и угловых ско­ростей звеньев.

4.Определение ускорений отдельных точек звеньев и угловых ус­корений звеньев.

Пример: Дана схема (рис. 2.1), длины звеньев l _O1A = 0,1 м, l _AВ = 0,28 м, l _ВО3 = 0,24 м, l _СО3 = 0,18 м, l _СD = 0,28 м, n = 400 об/мин. Исследова­ние механизма производится в 10-м положении.

По рядок расчета:

1. Выбираем масштаб для построения кинематической схемы, определяемый по формуле

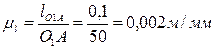
где l _{O1A =} 0,1— истинная длина звена;

О₁А = 50 мм — длина звена на чертеже.

2. В этом масштабе вычерчиваем планы механизма (рис. 2.1, а) в 12 равноотстоящих положениях кривошипа. За нулевое следует принять одно из крайних положений механизма. Для этого необходимо найти длины от­резков всех остальных

звеньев механизма, которые будут изображать их на чертеже:

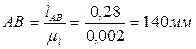
и так далее.

Для того, чтобы найти правое крайнее положение механизма, нужно из точки О₁; отрезком длиной 0₁А+АВ сделать засечку на дуге ра­диуса О₃В. Получим точку В₀ для нулевого положения. Затем найдем все остальные положения звеньев механизма. С помощью засечки длиной АВ—0₁А на дуге радиуса О₃В определим левое крайнее положение точки В и обозначим ее через В₃.

3. Производим структурный анализ. Так как заданный механизм плоский и относится к третьему семейству, то степень свободы меха­низма определяется по формуле Чебышева

где n — число подвижных звеньев, равное в данном механизме 5;

p₅—число кинематических пар 5-го класса (низшие кинематиче­ские пары). В данном механизме их 7 (0—1, 1—2, 2—3, 3—4, 3—0, 4—5, 5—0);

р₄—число кинематических пар 4-го класса (высшие кинематиче­ские пары), их в механизме нет. Тогда:

Рис. 2.1. Кинематическое исследование рычажного механизма методом планов:

а —кинематическая схема; б — группы Ассура; в — план скоро­стей; г — план ускорений

В данном механизме нет лишних степеней свободы и пассивных связей.

Проведем разложение механизма на структурные группы Ассура. Разложение следует начинать с отделения группы, наиболее отдаленной от ведущего звена. Разложение будет правильным, если после отделения каж­дой группы оставшаяся часть представляет собой кинематическую цепь с тем же числом степеней свободы, что и исходный механизм. По­этому раз­ложение необходимо начать с попытки отделения групп 2-го класса (двух-поводковых). В случае неудачи следует отделить группу 3-го класса или 4-го класса.

На рис. 3.1,б показано разложение механизма на структурные группы. Формула строения механизма имеет вид 1(0,1)®2₂₁ (2,3)®2₂₂ (4,5), т. е. к исходному механизму

1-го класса (звенья 0,1) присоединя­ются группы Ассура 2-го класса, состоящие из звеньев 2 — 3 (2-го по­рядка, 1-го вида) и 4— 5 (2-го порядка, 2-го вида). По классификации Ассура-Арт­обо­левского данный механизм является механизмом 2-го класса. Струк­турный анализ механизма всегда предшествует кинематическому исследо­ванию.

Кинематическое исследование механизма необходимо начинать с механизма 1-го класса, т. е. с ведущего звена. Задачи кинематического и силового исследования механизма в каждом положении его ведущего звена решаются для каждой группы Ассура отдельно, согласно формуле строе­ния.

Рассмотрим построение кинематических диаграмм. По найденным на пла­нах механизма (рис. 2.1,а) положениям ведомого звена 5 вычерчиваем гра­фик перемещения ползуна D (рис. 2.2,а), начиная от крайнего правого по­ложения. Так как по условию w₁=const, то ось абсцисс является не только осью углов (j поворота кривошипа, но и осью времени t).

Время оборота ведущего звена (кривошипа O₁A) в секундах, най­дем по формуле

Это время рекомендуется изображать на оси абсцисс отрезком

x = 0—12 = 120...180 мм; тогда масштаб времени, с/мм

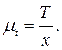
Масштаб перемещений, откладываемых по оси ординат, берем та­ким же, что и масштаб длины на схеме механизма, или изменяем.

Дифференцируя график перемещений, получим график изменения скорости ведомого звена. Дифференцирование проводим графически мето­дом хорд.

Последовательность построения графика V_D = V_D (t) (рис.2.2,б):

1. Проводим секущие (хорды) 0a, аb, bс, сd, df и т. д.

2. Выбираем полюс р_v на расстоянии H_v, которое рекомендуется брать порядка 20...40 мм, и проводим из него лучи 1, 2, 3, 4 и т. д., параллель­ные секущим 0a, аb, bс, сd, df и т.д., до пересечения с осью ординат.

3. Из точек пересечения 1, 2, 3 и т. д. проводим горизонтали до пере­сечения с вертикальными прямыми, проведенными из середин 0—1, 1—2 и т. д. отрезков времени Dt.

4. Точки пересечения 1', 2', 3', 4' и т. д. соединяем плавной кривой. Это будет кривая изменения скорости ведомого звена.

5. Вычисляем масштаб скорости, мс^-1/мм,

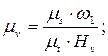
где w₁ - угловая скорость звена 1,

m_s — масштаб перемещений;

m_t — масштаб времени;

H_v—полюсное расстояние, мм.

Масштаб графика скорости зависит от выбора полюсного рас­стояния. Чем больше полюсное расстояние, тем меньше численный мас­штаб и тем большие ординаты имеет график скорости. Начальная и ко­нечная точки графика за период цикла движения механизма должны иметь одинаковые ординаты (в данном случае они равны нулю).

Аналогичным способом получим кривую ускорения (рис.2.2,в), дифференцируя график скорости. График ускорения, постро­енный путем графического дифференцирования кривой графика скоро­сти, изображает закон изменения лишь касательного ускорения. Только в случае прямолинейного движения точки, когда нормальное ускорение равно нулю, построенный график отобразит (как в нашем примере) закон изменения полного ускорения. Начальная и конечная точки графика ус­корения за время цикла движения механизма должны иметь одинаковые ординаты.

Масштаб графика ускорений, мс^-1/мм, определяется по формуле

Рис. 2.2. Кинематические диаграммы

Рассмотрим построение плана скоростей для 10-го положения (рис. 2.1,в).

Величина скорости точки A, м/с, перпендикулярной кривошипу 0₁A, определяется по формуле

(2.1)

.

Для построения плана скоростей выбираем на плоскости произ­вольную точку р — полюс плана скоростей, который является началом плана скоростей. Из полюса откладываем отрезок рa, изображающий на плане скоростей вектор скорости V_A. Он перпендикулярен звену 0₁А.

Тогда масштаб плана скоростей, мс^-1/мм

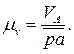(2.2)

Рассмотрим первую группу звеньев (звенья 2 и 3).

Для определения скорости точки В напишем два векторных урав­нения согласно теореме о сложении скоростей при плоско­параллельном движении:

(2.3)

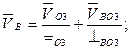(2.4)

Векторы относительных скоростей V_ВA и V_BO3 известны только по направлению. Вектор относительной ско­рости V_ВA перпендикулярен звену AВ, а вектор V_ВОЗ — звену О₃В.

Точка О₃ неподвижна, поэтому V₀₃=0. Таким образом, рассматри­ваемая группа присоединена к двум точкам, скорости которых известны и по направлению, и по величине.

В соответствии с векторным уравнением (2.3) на плане скоростей прово­дим через точку (а) прямую, перпендикулярную звену AВ. Это есть ли­ния вектора V_BA. В соответствии с векторным равенством (2.4) про­водим через точку О₃ на плане скоростей прямую, перпендикулярную звену O₃B. Это будет линия вектора V_ВОЗ. Точка (в) пересечения этих двух пря­мых и будет определять конец вектора, изображающего на плане скоро­стей вектор Vв. Чтобы определить истинную величину любого из векто­ров в м/с, надо его длину умножить на масштаб плана скоростей.

Напри­мер,

Для определения скорости точки С воспользуемся тем, что кар­тина относительных скоростей образует на плане скоростей фигуру, по­добную фигуре звена и повернутую относительно ее на 90° в сторону вращения звена. В соответствии с этим отрезок рb плана скоростей раз­делим в отно­ше­нии О₃В: O₃C, т. е.

Откуда

Величина скорости точки С, м/с

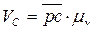
Перейдем к группе (звенья 4 и 5).

Для определения скорости точки D напишем векторные уравнения

(2.5)

(2.6)

Вектор относительной скорости V_DC и вектор абсолютной скорости V_D не известны по величине, но известны по направлению. В соответствии с векторным уравнением через точку С на плане скоростей проводим пря­мую, перпендикулярную звену CD. Это будет линия относительной скоро­сти, где далее проводим линию параллельно направляющей

Х-Х. Точка d, пе­ресечения этих прямых и есть искомая точка. Истинная величина скорости точки D, м/с

Определим угловые скорости. Угловая скорость звена 2, рад/с, оп­ределяется по формуле

(2.6)

Чтобы определить направление угловой скорости w₂, следует век­тор относительной скорости V_BA перенести в точку В механизма, а точку A мысленно закрепить. Тогда вектор V_BA будет стремиться вращать звено 2 по ходу часовой стрелки. Это и будет направление угловой ско­рости w₂

Остальные угловые скорости:

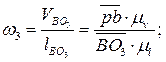(2.7)

(2.8)

Угловая скоростьw₃ направлена по часовой стрелке, w₄ — против.

Дата добавления: 2014-12-26