Рассмотрим построение плана ускорений

Для первой группы звеньев (звенья 2, 3), ускорение точки A, м/с² можно определить по величине и направлению.

Так как w₁=const, то

(2.9)

Точка О₃ неподвижна, следовательно, ускорение ее равно нулю.

Таким образом, группа присоединена к точкам, ускорения кото­рых известны.

Для построения плана ускорений выбираем на плоскости произ­вольную точку p — полюс плана ускорений (рис.3.1,г). Из полюса откла­дываем отрезок pа, изображающий на плане ускорений вектор ускорений точки A - a _A. Ускорение a _A направлено вдоль звена O₁A от точки A к точке O₁ (к центру вращения звена I). Тогда масштаб плана ускорений, мс^-1/мм,

(2.10)

Для определения ускорения точки В напишем два векторных

уравнения, рассмотрев движение точки В относительно точек A и О₃:

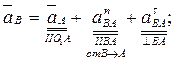(2.11)

(2.12)

Нормальные ускорения можно определить по величине и направ­ле­нию. Величина вектора

(2.13)

Вектор a ⁿ_BA направлен вдоль звена AВ от точки В к точке A (к цен­тру относительного вращения).

Величина вектора W_BO3определяется по формуле

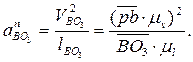(2.14)

Вектор a ⁿ_BA направлен вдоль звена ВA от точки В к точке A как к центру вращения. Тангенциальные ускорения не известны по величине, но известны по направлению. Из конца вектора a _A, ускорения точки A про­водим прямую, параллельную звену AВ — вектор нормального ускорения точки В относительно точки A(a ⁿ_BA), масштабная величина которого an₂ = a ⁿ_BA /m_W, измеряется в миллиметрах.

Через точку n₂ проводим направление вектора W^t_BA перпендикулярно звену ВA. Затем строим сумму векторов правой части векторного уравне­ния (2.11). Для этого проводим из полюса параллельно звену О₃В вектор a ⁿ_BO3. Его масштабная величина на плане ускорений pn₃ = a ⁿ_ВОЗ/m_W. Затем через точку n₃ перпендикулярно звену О₃В проводим вектор тангенци­аль­ного ускорения a ^t_BO3. Пересечение векторов a ^t_BO3 и a ^t_BA определит точку b. Вектор n₂b выражает ускорение a _BA, а вектор n₃b выражает уско­рение a ^t_BO3 Если соединить точку а с точкой b на плане ускорений, то вектор аb выра­зит полное относительное ускорение a _BA, так как является геометрической суммой векторов a ⁿ_BA и a ^t_BA. Подобно этому вектор o₃b на плане ускорений представляет масштабное выражение вектора пол­ного относительного ус­корения a _BO3. И, наконец, вектор pb выражает на плане ускорений вектор абсолютного ускорения точки В.

Для определения ускорения точки С воспользуемся свойством по­добия. На основании теоремы подобия имеем

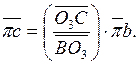
Тогда

Для определения ускорения точки D напишем векторное уравне­ние

(2.15)

Рассмотрим векторы, входящие в данное уравнение. Вектор W_C мы определили ранее. Величина вектора Wⁿ_DC, м/с², определяется по формуле

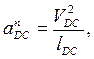(2.16)

а остальные векторы известны только по направлению.

Достраиваем план ускорений. Из точки с параллельно звену DC проводим вектор a ⁿ_DC, масштабная величина которого, мм, на плане ус­ко­рений равна cn₄ = a ⁿ_DC /m_W

Через точку перпендикулярно звену CD проводим вектор a ^t_DC, а через точку p параллельно направляющей — вектор a _D. На пересечении векторов a ^t_DC и a _D получим точку d, которая определит их ве­личины. По­лученный вектор n₄d на плане ускорений выражает в масштабе ускорение a ^t_DC, а вектор pd является изображением вектора ускорения a _D. Если соединить точку (с) с точкой (d), то вектор сd будет изображать пол­ное от­носительное ускорение a _DC.

Определим угловые ускорения. Ведущее звено 7 вращается с по­стоянной угловой скоростью, поэтому его угловое ускорение e₁=0.

Угловое ускорение звена 2, с^-2, равно величине тангенциального (касательного) ускорения a ^t_BA, деленной на длину звена AB, т.е.

___

a ^t_ВА n ₂ b m _a

e ₂ = ^¾¾¾¾ = ^¾¾¾¾¾. (2.17)

l _ВА l _ВА

Чтобы определить направление углового ускорения e₂, вектор от­но­сительного ускорения a ^t_BA следует перенести с плана ускорений в точку В механизма, а точку A мысленно закрепить. Тогда вектор a ^t_BA бу­дет стре­миться вращать звено 2 против хода часовой стрелки. Это и бу­дет направ­ление e₂.

Подобным образом находим угловые ускорения остальных звеньев;

___

a ^t_ВОЗ n ₃ b ·m _a

e₃ = ^¾¾¾¾ = ^¾¾¾¾¾; (2.18)

l _ВОЗ l _ВОЗ

___

a ^t_DC n ₄ b ·m _a

e₄ = ^¾¾¾¾ = ^¾¾¾¾¾; (2.19)

l _DC l _DC

e₃ и e₄ направлены против хода часовой стрелки.

Раздел 3. Синтез кулачковых механизмов

Дата добавления: 2014-12-26