Устойчивость замкнутой импульсной системы и ее предельный коэффициент. Годографы импульсной разомкнутой системы

Годографы импульсной разомкнутой системы

Годограф импульсной разомкнутой системы построим двумя способами:

· точным (непосредственно по найденной ранее передаточной функции)

· приближенным – по формуле:

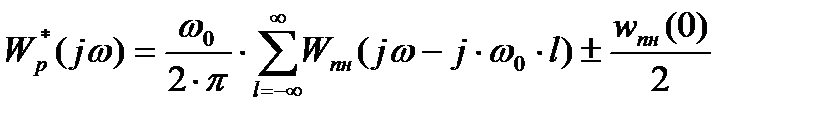
или в приближении:

,

В формуле ставится знак «+», если в приведенной непрерывной части системы отсутствует запаздывание, и «-» - в противном случае. В нашем случае .

Годографы для 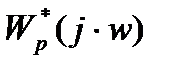и

Рис. 10

Как видно из рисунка 10, годографы импульсной разомкнутой системы, построенные точным и приближенным методом совпадают.

Численные значения амплитудно - фазовых характеристик импульсной разомкнутой системы, построенных точным и приближенным методами:

Точный метод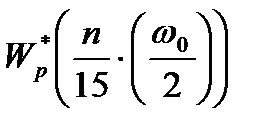

Приближенный метод

по критерию Найквиста:

Так как годограф разомкнутой импульсной системы не охватывает точку (-1;j0), то замкнутая система устойчива.

Значение предельного коэффициента усиления разомкнутой импульсной системы можно найти из пропорции:

, откуда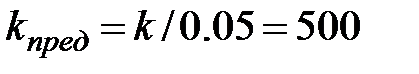

по критерию Гурвица:

Найдем передаточную функцию замкнутой ИСАУ, выделив коэффициент усиления разомкнутой системы k_p:

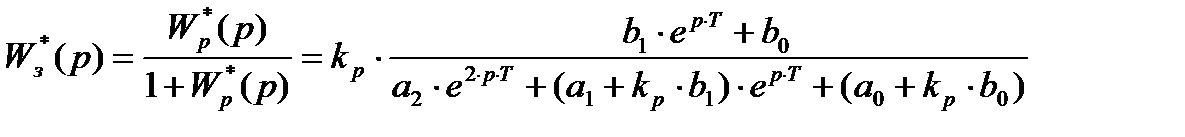
Введем обозначение и запишем характеристическое уравнение:

Произведем подстановку:

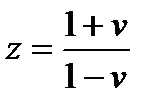
где

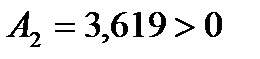
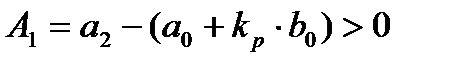
Так как все коэффициенты положительны, то замкнутая ИСАУ устойчива.

Наиболее просто из приведенных выше формул найти значение предельного коэффициента усиления, которое получаем из уравнения:

,

На основе необходимого и достаточного условия устойчивости системы (в плоскости “Z”)

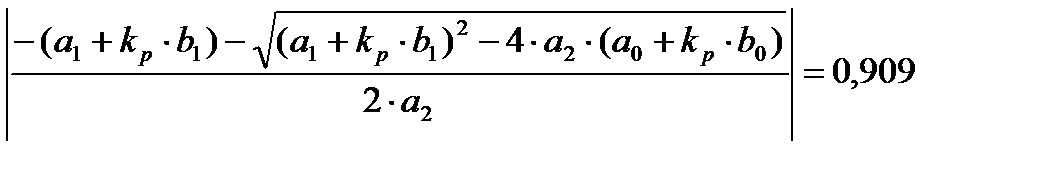
Корни не выходят из круга радиуса 1, следовательно, система устойчива. Предельный коэффициент усиления k₃ получаем из решения уравнения:

,

Переходной процесс на выходе замкнутой ИСАУ (x_p(t))

Найдем передаточную функцию замкнутой ИСАУ относительно выходного сигнала x_p(t)::

.

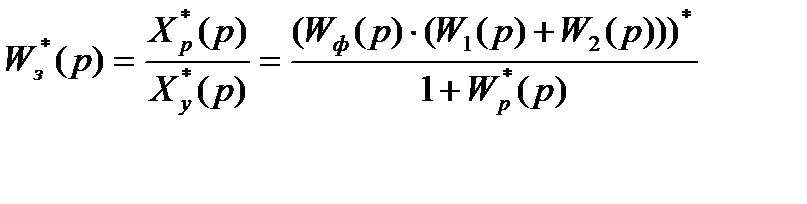Поскольку передаточную функцию 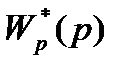мы нашли ранее, определим дискретную передаточную функцию числителя, т.е. .

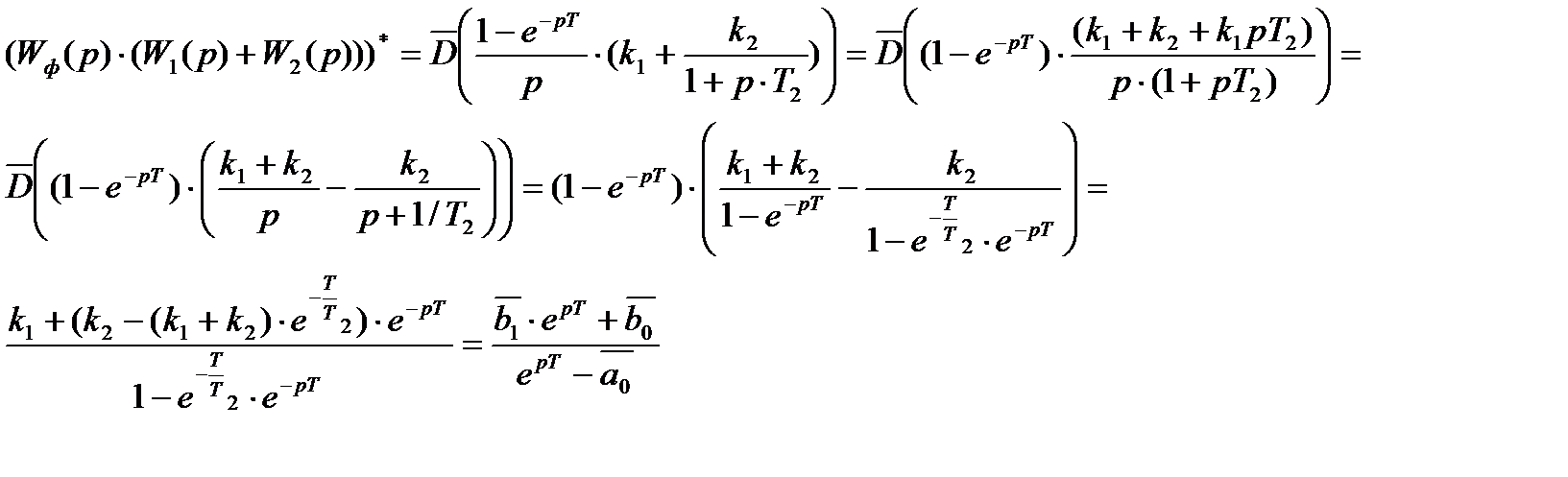где ;

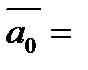
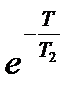
Таким образом, дискретная передаточная функция замкнутой системы относительно выходного сигнала x_p(t) имеет вид:

Перейдем от изображения к оригиналу:

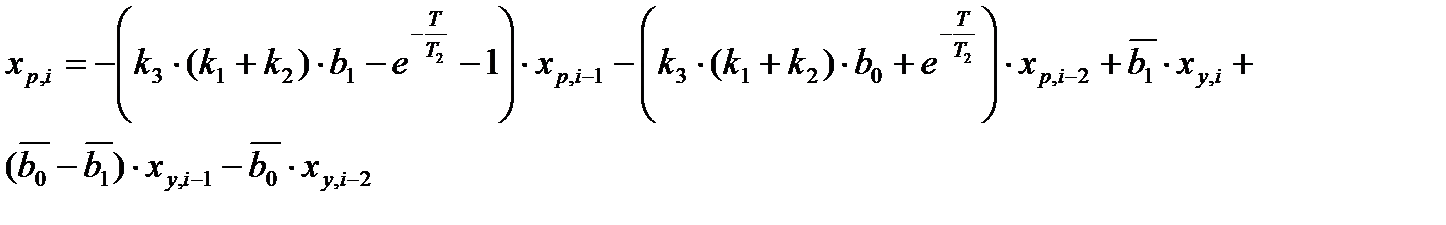
График переходного процесса, построенный на основе последнего соотношения, изображен на Рис. 11

Переходной процесс в замкнутой ИСАУ

Рис. 11

Кинетическая и статическая ошибки замкнутой ИСАУ (x_уст=x_y-y)

– Статическая

На входе системы X_y(t)=1(t)

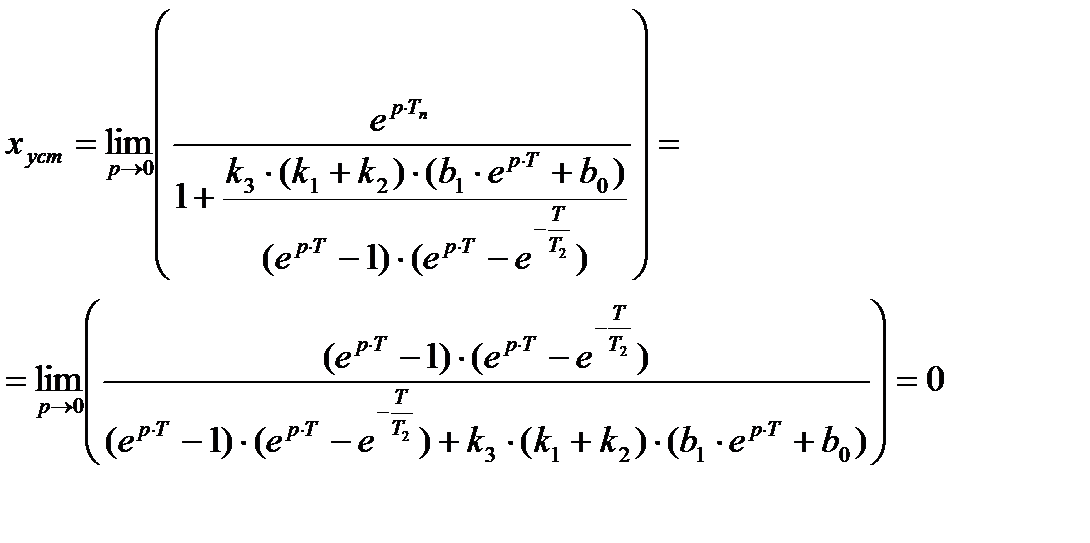
– Кинетическая

На входе системы X(t)=t×1(t)

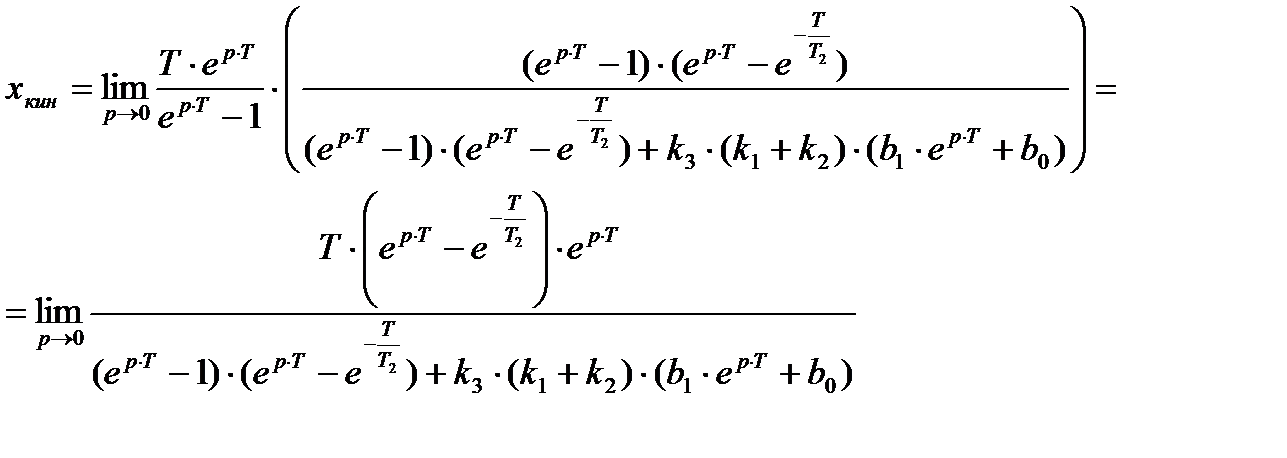
Численные значения переходного процесса в определенные моменты времени (i:=0,2,40) замкнутой ИСАУ:

Дата добавления: 2014-12-26