Устойчивость замкнутой импульсной системы и ее предельный коэффициент

Определим устойчивость замкнутой САУ и предельный коэффициент усиления ():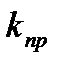

По критерию Найквиста:

Так как АФХ 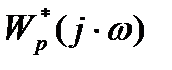охватывает точку с координатами (-1,j0), а разомкнутая импульсная САУ находится на границе устойчивости, то рассматриваемая САУ в замкнутом состоянии является неустойчивой.

Предельный коэффициент можно определить согласно следующему соотношению:

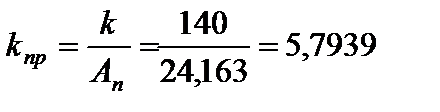
где 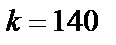– коэффициент усиления разомкнутой САУ; 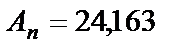– модуль комплексного коэффициента усиления при его аргументе равном -180⁰.

По критерию Гурвица:

Запишем передаточную функцию дискретной САУ в замкнутом состоянии через Z–преобразование (относительно сигнала y):

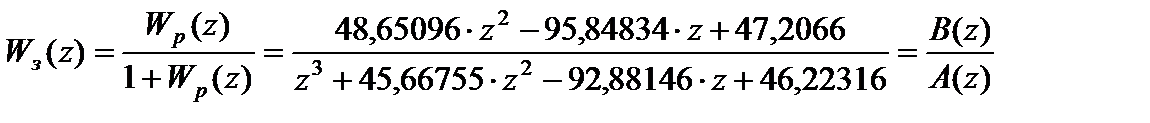
Введем подстановку 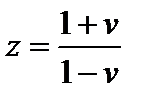. Тогда характеристическое уравнение 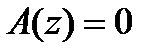принимает вид:

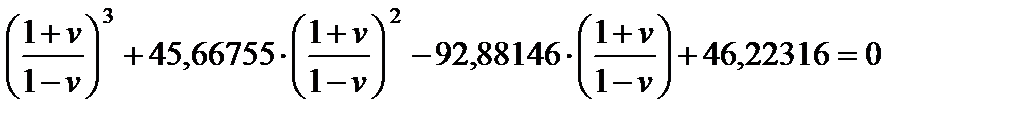
После преобразований, из последнего соотношения получим:

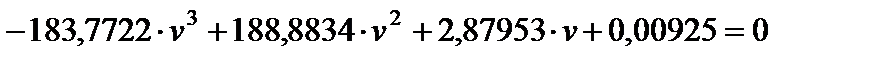
Так как характеристическое уравнение устойчивой системы 3-го порядка имеет все положительные коэффициенты, то рассматриваемая система является неустойчивой в замкнутом состоянии.

Определим 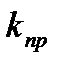. Для этого передаточную функцию разомкнутой импульсной САУ при 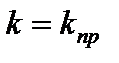представим следующим образом:

.

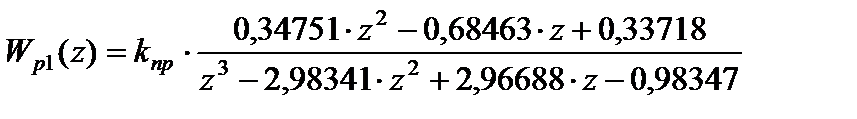Тогда соответствующая передаточная функция САУ в замкнутом состоянии 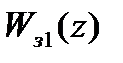примет вид:

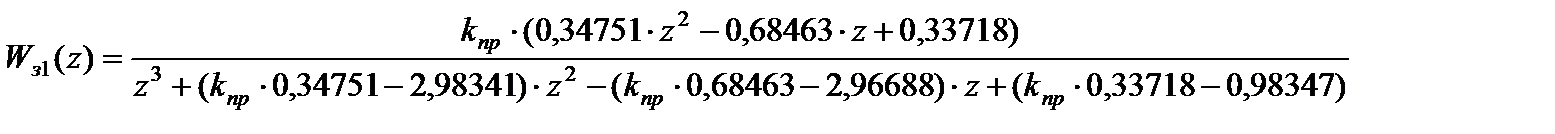
Подставим в характеристическое уравнение соответствующее передаточной функции 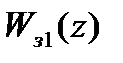, 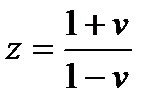. Тогда, после преобразований, получим:

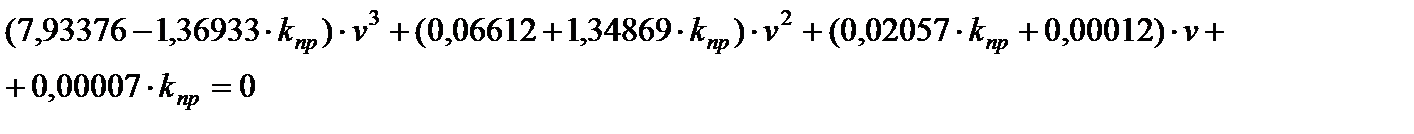
Так как для САУ 3-го порядка условие устойчивости сводится к положительности коэффициентов характеристического уравнения и выполнению неравенства a_1*a₂-a_0*a₃>0, где a₀= 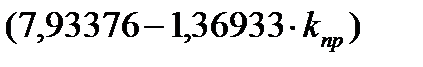; a₁= ;

a₂= ; a₃= 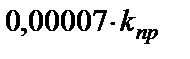, которое выполняется,

то из коэффициента при старшей степени получаем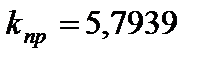

На основе необходимого и достаточного условия устойчивости системы (в плоскости “Z”):

Найдем корни характеристического уравнения замкнутой системы:

.

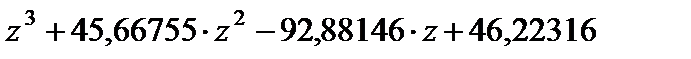Корни, равные (-46,986; 0,9790; 0,9907) выходят из окружности единичного радиуса, значит, замкнутая система неустойчива.

Возьмем 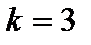и для этого коэффициента усиления разомкнутой системы определим устойчивость замкнутой системы на основе корней характеристического уравнения.

Для 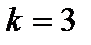получим, что:

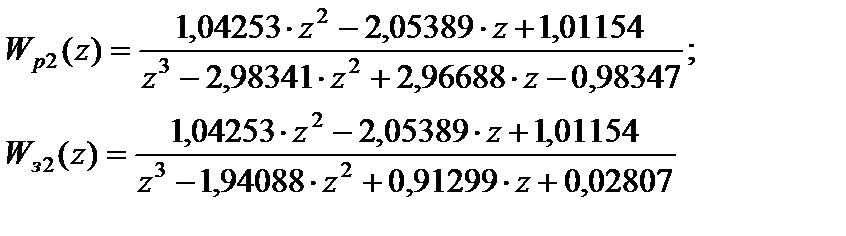
Откуда корни характеристического уравнения для замкнутой системы равны:

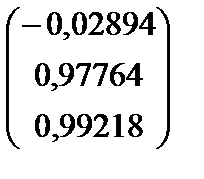, т.е. 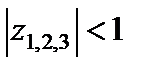– значит, замкнутая САУ является устойчивой.

Переходной процесс на выходе замкнутой ИСАУ (x_p(t))

Построим переходной процесс на выходе замкнутой импульсной САУ x_p(t) при .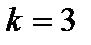

Для этого найдем дискретную передаточную функцию прямой цепи заданной системы, т.е. =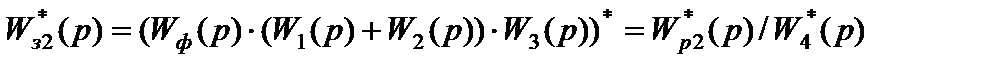

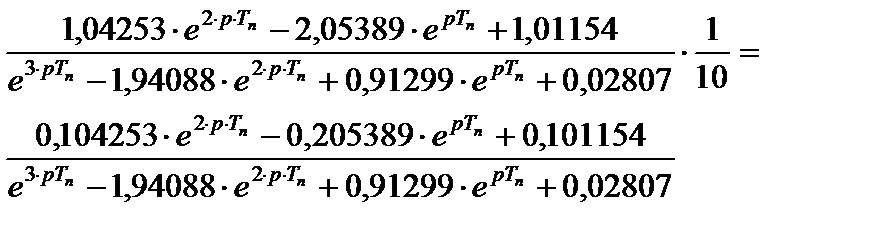
Запишем эту передаточную функцию относительно аргумента z и разделим числитель и знаменатель на 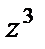. Тогда

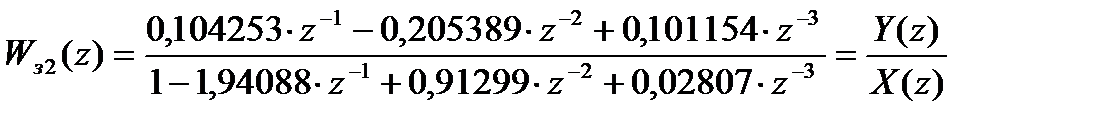
Переходной процесс можно построить по следующему разностному уравнению, полученному из выражения для :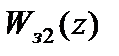

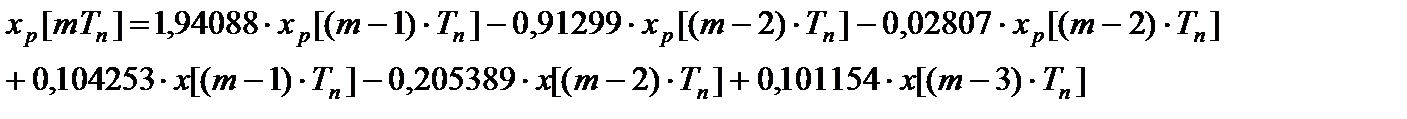
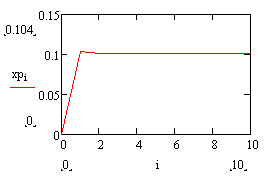
Рис. 18

Кинетическая и статическая ошибки замкнутой ИСАУ (x_уст=x_y-y):

Передаточная функция системы относительно ошибки равна:

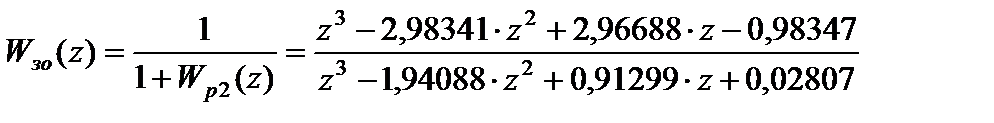
Тогда статистическая ошибка при :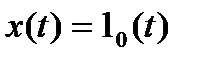

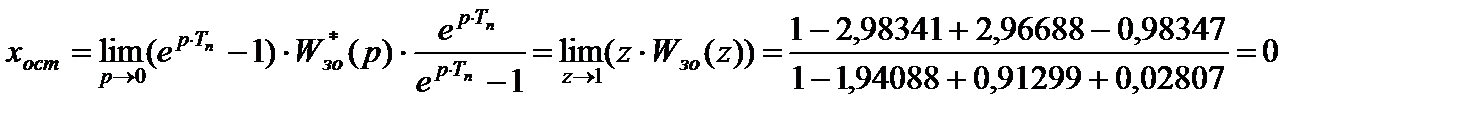
Кинетическая ошибка имеет место, когда входной является функция, изменяющаяся по линейному закону:

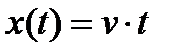или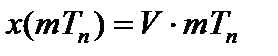

Дискретное преобразование Лапласа указанного сигнала:

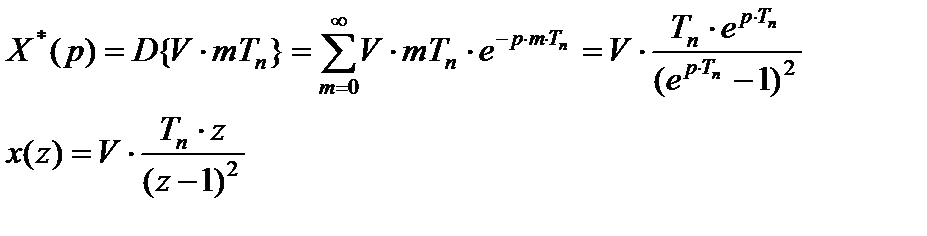
С учетом этого кинетическая ошибка будет равна:

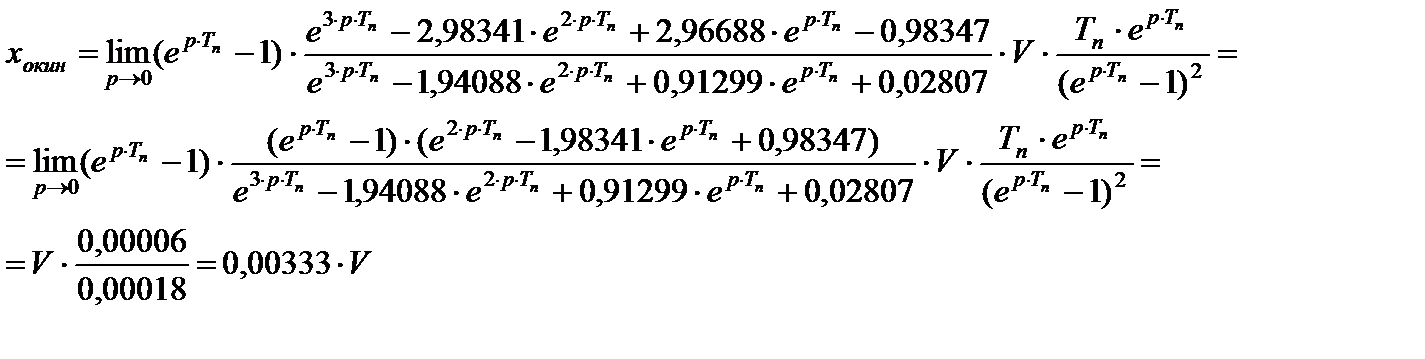
Дата добавления: 2014-12-26