
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вектора. Длина вектора
|
|
|
|
Произведение вектора на число.
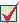
Сложение векторов.
 Суммой двух векторов
Суммой двух векторов  и
и  называется вектор
называется вектор  , соединяющий начало вектора
, соединяющий начало вектора  с концом вектора
с концом вектора  , отложенного от конца вектора
, отложенного от конца вектора  .
.
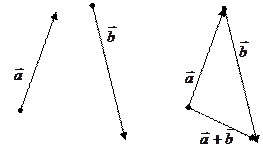
 |
Произведени  ем вектора
ем вектора  на число
на число 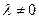 называется вектор, который имеет длину
называется вектор, который имеет длину  и который имеет направление вектора
и который имеет направление вектора  в случае
в случае  и противоположное направление в случае
и противоположное направление в случае  .
.
Пример 3.1. Даны векторы  и
и  .
.
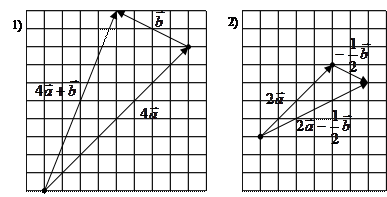
 Постройте векторы: 1)
Постройте векторы: 1)  ;
;
2) 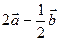 .
.


 § 2. Декартовы прямоугольные координаты
§ 2. Декартовы прямоугольные координаты
Пусть вектор  составляет угол
составляет угол 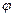 с осью
с осью  .
.
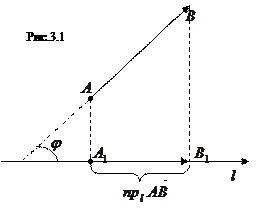
 Проекцией вектора
Проекцией вектора  на ось
на ось  называется число, равное длине вектора
называется число, равное длине вектора 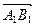 (рис.3.1), взятой со знаком «плюс», если направление вектора
(рис.3.1), взятой со знаком «плюс», если направление вектора  совпадает с направлением оси и со знаком «минус» в противном случае.
совпадает с направлением оси и со знаком «минус» в противном случае.
 Проекцию вектора
Проекцию вектора  на ось
на ось  можно вычислить по формуле:
можно вычислить по формуле:
 .
.
 Декартовыми прямоугольными координатами
Декартовыми прямоугольными координатами  вектора
вектора  называются его проекции на соответствующие координатные оси
называются его проекции на соответствующие координатные оси 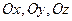 .
.
 Вектор
Вектор  с координатами
с координатами  записывают в виде
записывают в виде 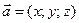 или
или 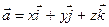 , где
, где 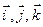 — единичные векторы координатных осей
— единичные векторы координатных осей 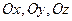 соответственно. Длина вектора
соответственно. Длина вектора  определяется по формуле:
определяется по формуле:
 .
.
Если вектор  задан точками
задан точками  и
и 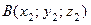 , то его координаты вычисляются по формулам:
, то его координаты вычисляются по формулам:

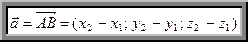 .
.
Пример 3.2. Даны две точки 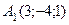 и
и  . Найдите координаты и длину вектора
. Найдите координаты и длину вектора 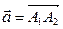 .
.
 По условию задачи
По условию задачи  ,
, 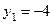 ,
,  ,
,  ,
,  ,
,  . Значит,
. Значит,  .
.
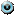
 .
.
Пример 3.3. Даны два вектора  и
и  . Найдите координаты и длину вектора
. Найдите координаты и длину вектора  .
.

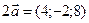 ;
;  ;
;
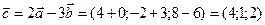 ;
;
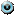
 .
.
 Совместим параллельным переносом начало некоторого вектора
Совместим параллельным переносом начало некоторого вектора 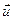 с началом координат прямоугольной системы координат
с началом координат прямоугольной системы координат  . Пусть
. Пусть 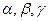 — углы, которые образует вектор
— углы, которые образует вектор 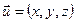 с осями координат
с осями координат 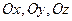 соответственно (рис.3.2). Направление вектора
соответственно (рис.3.2). Направление вектора 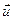 определяется с помощью направляющих косинусов
определяется с помощью направляющих косинусов 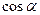 ,
,  ,
,  , для которых справедливы равенства:
, для которых справедливы равенства:
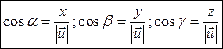 , ,
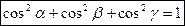 . .
| 
|
 § 3. Скалярное произведение векторов.
§ 3. Скалярное произведение векторов.

 Скалярным произведением двух ненулевых векторов
Скалярным произведением двух ненулевых векторов  и
и  называется число, равное произведению длин этих векторов на косинус угла
называется число, равное произведению длин этих векторов на косинус угла  между ними (см. рис.3.3):
между ними (см. рис.3.3):
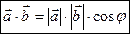 .
.

| 
|
 Из рис. 3.3 видно, что
Из рис. 3.3 видно, что  .
.
Поэтому 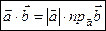 или
или  . (*)
. (*)
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 558; Нарушение авторских прав?; Мы поможем в написании вашей работы!