Деление отрезка в данном отношении

Направляющие косинусы, длина вектора.

Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х₁, y₁, z₁), B(x₂, y₂, z₂), то .

Направляющими косинусами вектора называются косинусы углов , образуемых им с координатными осями.

Принимая во внимание формулу 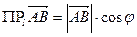, для вектора 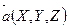получаем

Из полученных формул и формулы нахождения длины вектора находим формулы для направляющих косинусов вектора :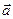

.

Возводя в квадрат и почленно складывая, имеем:

; следовательно, сумма квадратов направляющих косинусов вектора равна 1.

Из формул следует, что координаты единичного вектора равны его направляющим косинусам.

Если точка М(х, у, z) делит отрезок АВ в соотношении l, считая от А, то координаты этой точки определяются как:

В частном случае координаты середины отрезка находятся как:

x = (x₁ + x₂)/2; y = (y₁ + y₂)/2; z = (z₁ + z₂)/2.

Если l отрицательна, значит точка М лежит на продолжении отрезка АВ.

Дата добавления: 2014-12-26