Волны напряжения и тока в линии. Бегущие и стоячие волны

Коэффициенты и в выражении для напряжения (9.11) имеют размерность напряжения, их можно выразить в показательной форме:

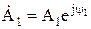и .

Тогда

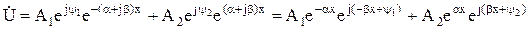. (9.13)

Перейдем от действующего значения напряжения к мгновенному:

. (9.14)

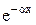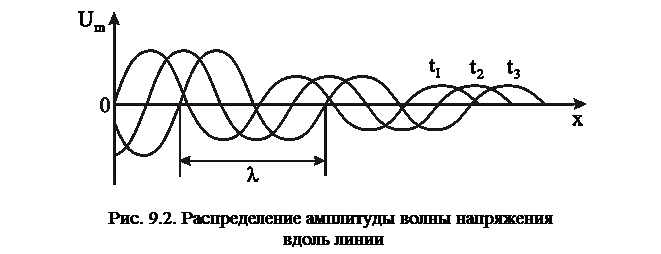
То есть напряжение (так же, как и ток) в линии в каждый момент времени является синусоидальной функцией координаты. Это синусоидальное распределение напряжения, или, как говорят, волна напряжения, перемещается вдоль линии. Волны такого рода называются бегущими. При a>0 наличие множителя показывает, что амплитуда волны вдоль линии затухает по показательному закону. Таким образом, коэффициент 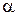характеризует изменение амплитуды волны напряжения (тока) и определяется в децибелах, деленных на единицу длины линии. Коэффициент b характеризует изменение фазы волны и определяется в радианах, деленных на единицу длины линии. Распределение напряжения такой волны вдоль линии может в любой момент времени быть изображено синусоидой, затухающей по тому же закону (рис. 9.2). С течением времени ( эта синусоида будет перемещаться в направлении увеличения координаты.

Основными характеристиками бегущей волны являются фазовая скорость u_ф и длина волны l. Фазовая скорость – это скорость перемещения фазы колебания, которая с течением времени t и с расстоянием x, пройденным волной, остается постоянной, то есть .

Тогда

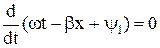(9.15)

и

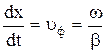. (9.16)

В линии могут существовать как прямые волны (движущиеся от начала к концу линии), так и обратные (движущиеся от конца линии). В выражении (9.14) первое слагаемое описывает прямую волну, а второе – обратную. Для обратных волн справедливо равенство:

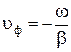. (9.17)

Фазовая скорость волны в воздушной линии , то есть близка к скорости света.

Длина волны в линии l – это расстояние между двумя ближайшими точками, взятое в направлении распространения волны, фазы в которых различаются на 2p:

. (9.18)

Длину волны l можно ещё определить как путь, который проходит волна за период T изменения напряжения или тока:

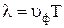. (9.19)

Отношение напряжения прямой волны к току прямой волны равно волновому сопротивлению линии; для обратных волн – со знаком «минус»:

; .

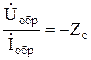Появление обратных волн можно рассматривать как результат отражения прямых волн от конца линии. Соответственно прямые волны называют также падающими, а обратные – отраженными:

; .

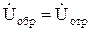Отражение может происходить как от нагрузки в конце линии, так и от любого сечения линии, в котором есть какая-либо неоднородность. Отношение отраженной волны к прямой волне напряжения называют коэффициентом отражения по напряжению :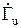

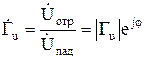, (9.20)

где и j – амплитуда и фаза коэффициента отражения.

Аналогично определяется коэффициент отражения по току .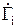

В конце линии:

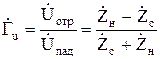; (9.21)

, (9.22)

где – сопротивление нагрузки линии. (В дальнейшем мы будем пользоваться только коэффициентом отражения по напряжению, обозначая его .)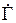

Видно, что если линия замкнута на сопротивление, равное волновому, то 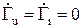. Это означает, что в линии будут отсутствовать отраженные волны. Такая нагрузка называется согласованной.

При этом в любой точке линии .

Введем понятие входного сопротивления линии 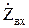: под ним понимают такое сосредоточенное сопротивление, которым можно заменить линию вместе с нагрузкой при расчете режима в начале линии. Тогда в произвольном сечении:

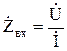; (9.23)

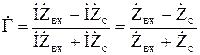. (9.24)

Отсюда

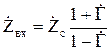. (9.25)

Дата добавления: 2014-12-26