Граничные условия

Под граничными понимают условия, которым подчиняется поле на границе раздела двух сред с разными электрическими свойствами.

Для упрощения решения задачи нахождения граничных условий векторы электромагнитного поля принято разлагать на нормальные и тангенциальные составляющие и рассматривать отдельно поведение нормальных и тангенциальных составляющих.

1. Граничные условия для нормальных составляющих векторов магнитного поля

Пусть S – поверхность раздела двух сред 1 и 2 (рис. 10.2). Выделим в окрестности точки А, лежащей на поверхности S, элементарный цилиндрический объём с основанием ΔS и высотой Δh.

Вектор магнитной индукции 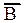представим в виде суммы нормальной и тангенциальной составляющих:

(10.1)

и рассмотрим поведение нормальной и тангенциальной составляющих отдельно. Поток магнитной индукции через суммарную поверхность элементарного цилиндра:

, (10.2)

где , – векторы магнитной индукции в средах 1 и 2; 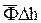– поток через боковую поверхность; 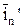, – единичные векторы нормали к поверхности раздела в средах 1 и 2 (). При 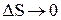приближенное равенство становится точным. При поток через боковую поверхность равен нулю – :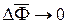

. (10.3)

Из закона непрерывности магнитных силовых линий

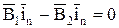или , (10.4)

то есть нормальные составляющие вектора магнитной индукции на границе раздела двух сред непрерывны.

Соответственно напряженность магнитного поля на границе раздела испытывает скачок – изменяется обратно пропорционально магнитной проницаемости:

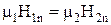. (10.5)

На границе с идеальным проводником H_n=0.

2. Граничные условия для нормальных составляющих векторов электрического поля

Методика определения граничных условий для нормальных составляющих электрического поля такая же, как и для магнитного поля, но для электрического поля . При наличии поверхностных электрических зарядов (r_пов¹0) можно записать аналогично случаю магнитного поля:

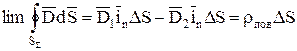, (10.6)

где ; q – заряд, располагающийся в поверхностном слое.

Тогда

. (10.7)

Это означает, что при наличии заряженной поверхности раздела двух сред нормальная составляющая вектора электрического смещения изменяется скачком на величину плотности поверхностного заряда в исследуемой точке.

На границе двух идеальных диэлектриков (r_пов=0)

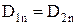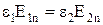; . (10.8)

На границе с идеальным проводником

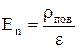; . (10.9)

3. Граничные условия для тангенциальных составляющих векторов магнитного поля

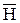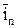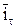Выделим в окрестностях точки A на границе раздела двух сред (рис. 10.3) достаточно малый (чтобы считать векторы в пределах его сторон постоянными) прямоугольный контур L со сторонами Dl и Dh в плоскости векторов и . Вектор 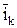образует нормаль к плоскости, образованной векторам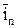и и 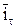, и лежит в плоскости границы раздела. В обеих областях (1 и 2) протекают токи, которые могут включать как токи проводимости, так и токи смещения. Применяя закон полного тока, получаем:

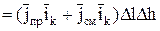. (10.10)

При

, (10.11)

Тогда

(10.12)

или

, (10.13)

то есть тангенциальные составляющие вектора напряженности магнитного поля на границе раздела двух сред непрерывны (в случае сред с конечной проводимостью).

Если же одна из сред – идеальный проводник, проводимость его бесконечна и глубина проникновения поля равна нулю на любой частоте. В результате токи проводимости протекают по поверхностному слою нулевой толщины, поэтому выражение (10.11) становится не равным нулю.

Для характеристики поверхностных токов вводят понятие плотности поверхностного тока:

, (10.14)

где – единичный вектор, касательный к линиям тока в данной точке; Dl – пересекаемый током отрезок линии, перпендикулярной к вектору .

Тогда формула для циркуляции вектора напряженности перепишется в виде:

. (10.15)

С учетом того, что поле в идеальном проводнике равно нулю ():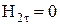

. (10.16)

Эта формула позволяет определить плотность поверхностного тока по известному магнитному полю на границе идеального проводника.

С учетом того, что 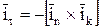, можно записать:

, (10.17)

то есть поверхностный ток на границе раздела с идеальным проводником протекает в направлении, перпендикулярном к вектору , и численно равен напряженности магнитного поля.

4. Граничные условия для тангенциальных составляющих векторов электрического поля

Методика определения граничных условий для тангенциальных составляющих векторов электрического поля такая же, как и для векторов магнитного поля, но вместо закона полного тока следует воспользоваться законом электромагнитной индукции. В соответствии с этим законом

, (10.18)

отсюда для границы раздела двух диэлектриков

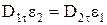; . (10.19)

На границе с идеальным проводником , то есть существует только нормальная составляющая вектора электрического поля.

Дата добавления: 2014-12-26