Дебиеттер тізімі 6 страница

Орташа индекстерді есептеу

Агрегатты индекстерді есептеу кезінде индекстелетін және оларды салмақтайтын абсолютті шамалары, яғни сатылған тауарлардың немесе өндірілген өнімдердің саны (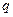), олардың бағасы (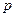) мен өзіндік құны () және т.б. көрсеткіштері белгілі болуы керек. Бірақ, кейбір жағдайларда бұл көрсеткіштердің сандық (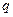) және сапалық (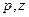) мәндері белгісіз болып, оның орнына өткен мерзімдегі тауар айналымы (), өндірілген өнімге жұмсалған жалпы шығын (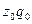) және сатылған тауарлардың көлемі (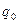) мен оның әр данасының бағасы (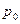) немесе өзіндік құны (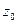) пайыз есебімен, өзгерген қалпында берілуі мүмкін. Мұндай жағдайда олардың өзгерісін анықтау үшін жеке (дара) индекстер бойынша есептелген көрсеткіштерді қолдана отырып, агрегатты индекстерді орташа индекстерге түрлендіреміз. Жеке (дара) индекстерді қолдану себебіміз, агрегатты индекстер арқылы есептелген көрсеткіштер жеке (дара) индекстердің орташа көрсеткіші болып табылады.

Статистикада агрегатты индекстерді орташа индекстерге түрлендіру арифметикалық және үйлесімдік (гармоникалық) тәсілдермен жүргізіледі.

Арифметикалық орташа индекс. Егер шығарылған өнімнің саны (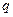) мен өзіндік құны () белгісіз болып, өткен мерзімдегі жалпы шығын () мен өндірілген өнім көлемінің өзгерісі () белгілі болатын болса, онда шығарылған өнім көлемінің өзгерісін анықтау үшін, көлемдік жалпы индексті қолданамыз:

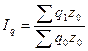(24)

Берілген формуланың алымы мен бөліміндегі көрсеткіштерге талдау жасайтын болсақ, онда бөліміндегі көрсеткіш (), яғни өткен уақыттағы жалпы шығын белгілі де, алымындағы () ағымда шығарылған өнімнің саны (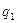) белгісіз. Бірақ әрбір өндірілген өнім көлемінің өзгергені жеке (дара) индекстің формуласынан (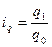), белгісіз 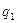тауып (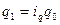), одан шыққан көрсеткішті бөлшектің алымына жазатын болсақ, формула мынадай түрде түрленеді:

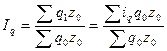
яғни өткен мерзімдегі жалпы шығынды көлемдік жеке (дара) индекске көбейту арқылы агрегатты индексті арифметикалық орташа индексті түрлендіреміз.

Үйлесімдік орташа индекс. Егер ағымдағы мерзімде шығарылған өнімнің саны (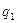) мен өзіндік құны (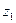) белгісіз болып, жалпы шығын (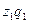) мен өнімнің өзіндік құнының өзгерісі (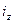), яғни өткен мерзіммен салыстырғандағы азаюы немесе көбеюі берілетін болса, онда мұндай көрсеткіштерді есептеу үшін, өзіндік құнның жалпы индексін үйлесімдік (гармониялық) орташа индекске түрлендіреміз. Ол үшін агрегатты индекстің 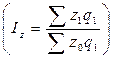бөліміндегі өткен уақыттағы өзіндік құнды есептеп алуымыз керек. Оны есептеу үшін өзіндік құнның жеке (дара) индексінен 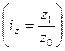, өткен мерзімдегі өзіндік құнды тауып, оны өзіндік құнның жалпы индекс формуласындағы бөлімінің орнына қоятын болсақ, онда үйлесімдік (гармониялық) орташа индекстің формуласы мынадай түрге түрленеді:

.

Тұрақты және өзгермелі құрамды индекстер

Экономикалық біртектес құбылыстар мен процестердің сапалық өзгерісін, сол көрсеткіштердің орташа дәрежесін салыстыру арқылы сипаттайды. Мысалы, бір аудандағы шаруашылықтардың дәнді дақылдар өнімдерінің орташа өзіндік құнының өзгеруі, немесе бірнеше базарда әр түрлі бағамен сатылған тауардың орташа бағасының өзгеруі және т.с.с.

Сонымен, экономикалық құбылыстардың орташа көрсеткіштерінің өзгерісін зерттегенде, оған әсерін тигізетін әрбір себептер (факторлар) жеке-жеке есептеледі. Статистикада бұл көрсеткіштер тұрақты және өзгермелі құрамды индекстер арқылы анықталады. Енді осы индекстердің қолданылуы мен есептелу тәсілдерін жеке қарастырайық.

Тұрақты құрамды индекс. Құбылыстың өзгеруіне әсерін тигізетін себепті анықтау үшін сапалық көрсеткіштер құрамын өзгермелі түрде алсақ, яғни салыстыратын екі уақыт мерзімдерінің шамасы алынса, ал салмағы ретінде ағымдағы кезеңнің тұрақты дәрежесі (көлемі) қолданылса, онда тұрақты индекс шығады және оны сапалық мәндері бойынша мына формулалар арқылы есептеуге болады.

· баға бойынша: (25)

· өзіндік құн бойынша: 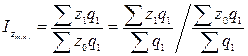және т.б. (26)

Өзгермелі құрамды индекс. Мұнда, статистикалық талдау жасау үшін, екі уақыт кезеңіндегі зерттелетін құбылыстың орташа шамалары жеке есептеледі, бірімен-бірі салыстырылады және олардың қандай себептерден өзгергені анықталады. Бұл индексте салмақталған екі орташа шаманың қатынасы қарастырылады. Сондықтан оны орташа шамалар индексі деп те айтады және ол мына формулалар арқылы есептеледі:

· баға бойынша:

· өзіндік құн бойынша: және т.б.

Құрылымның өзгеру индексі. Егер жиынтық құрамының өзгеру әсерінен орташа сапа көрсеткішінің өзгерісі анықталатын болса, онда оны құрылымның өзгеру индексі деп атайды. Бұл индексті есептеу үшін өзгермелі құрамды индексті тұрақты құрамды индекске бөлеміз.

Кейбір жағдайларда өзгермелі немесе тұрақты индекстердің көрсеткіштері есептелінбеуі мүмкін. Онда құрылымның өзгеру индексін есептеу үшін мына формулалар қолданылады:

· өзіндік құн бойынша:

(27)

өзгермелі құрамды тұрақты құрамды құрылымның өзгеру

индекс индекс индексі

· баға бойынша:

(28)

өзгермелі құрамды тұрақты құрамды құрылымның өзгеру

индекс индекс индексі және т.б.

Сонымен, бұл индекстердің әрқайсысының белгілі бір экономикалық мәселені шешуде атқаратын рөлі өте жоғары және бұл түрлі басқару жұмыстарына талдау жасауда жиі қолданылады. Мысалы, өзгермелі құрамды индекс жалпы сапалық көрсеткіштердің орташа өзгерісін, ал тұрақты құрамды индекс сапалық көрсеткіштердің орташа өзгерісін сол жиынтық құрамының тұрақтылығы арқылы көрсетеді. Яғни сапа көрсеткіштері өзгерістерінің қандай себептер әсерінен болғандығын анықтайды.

Негізгі әдебиеттер 3 [105-118], 5 [65-98];

Бақылау сұрақтары:

1. Өзара байланысты индекстердің жүйесі;

2. Баға құрылымының өзгерісіне индекстің әсері;

3. Бағаның агрегатты индексінің тауар айналымынан тәуелділігі.

4. Орташа шамалар индексі қандай

5. Үйлесімдік орташа индексқандай

11. Дәріс тақырыбы. Жұп сызықтық регрессия теңдеуі және ең кіші квадраттар әдісі бойынша модель.

Дәріс конспектілері: Басқада оңтайлы шешімдер бар, дегенмен, ең кіші квадраттар әдісін қолдану ығыспаған тиімді a және в бағаларын береді. Осы себептерге байланысты, регрессиялық талдау кезінде ең кіші квадраттар әдісі жиі қолданылады.

Қатардың өсіңкілік көрсеткіштерін уақытқа байланысты тегістеуде (тренд) және болжау үшін екі әдіс қолданылады:

а) аналитикалық;

ә) ең кіші квадрат әдісі.

Эмперикалық мәліметпен есептелген өсіңкілік қатар көрсеткіштері арасында өте тығыз байланыс бар, уақытқа тәуелді байқалуы 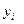пен 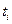-лердегі байланыс пен тәуелділікте. Аналитикалық тегістеу (тренд) өсіңкі қатар көрсеткішінің орташа өзгерісін бақылау арқылы, болашақты бағдарлауға негізделген. Мұндай өсіңкі қатарды тегістеу көп жағдайда орташа шаманың жылжуына қарай, оның сандық, сапалық талдау арқылы, экономиалық өзгерістің нақты және қатысты шамаларын ескере отырып алдағы уақытқа (ай, жыл, т.б.) болжам жасауға болады. Ең кіші квадраттық ауытқу әдісін пайдаланып, тегістеуде

функциясын немесе

(29.1)

теңдеуін аламыз. Мұнда в ₀ –бос мүше, в ₁-теңдеу коэффициенті, t – уақыт өлшем бірлігі,

t = 1,2,…,n тең (29) теңдеуінен ең кіші квадраттық ауытқу (ЕКК)арқылы былай жазуға болады.

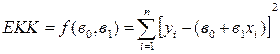(29.2) немесе оны кейде ең кіші квадраттар әдісінің критерийі түрінде жазуға болады.

(29.3)

Бұдан жоғарыдағы (29.2) теңдеуді в ₀, в ₁ арқылы диференциалдаймыз, келтірілген сызықты теңдеулер жүйесін жазамыз

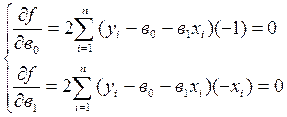(29.4)

(29.4) – үшін келтірілген теңдеу жүйесін жазуға болады:

(30)

Егер 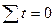, онда уақыт өлшемін – 1, -2, 0, +2, +1 деп аламыз.

(30) жүйе мына түрге келеді:

Бұдан: (31)

Мысал-7. Құрылыс компаниясы үй салудағы өсіңкілік қатарды теориялық (ЕКАӘ) әдісімен тегістеу, болжау (млн м²).

Шешуі.

11- кесте

Жылдар	Құрылыс компаниясы салған үйлер млн кв м.	Уақыт ti	yiti	ti^2	Өсіңкі тегістеу yi	Ауытқу (yi-yi)	ЕКАӘ (yi-yi)^2
	2,9	-2	-5,8		2,76	0,14	0,019
	2,4	-1	-2,4		2,49	-0,09	0,008
	2,1				2,22	-0,12	0,014
	1,9		1,9		1,95	-0,05	0,002
	1,8		3,6		1,68	0,12	0,014
Барлығы	11,1		-2,7		11,10	0,00	0,059

11-кестеден 2,4,5 бағаналарды қолданып, түзу сызық теңдеуінің параметрлерін есептейміз:

.

Өсу (динамикалық) қатарының параметрлерін мәндерін (29.1) –ге қойып түзу сызық теңдеуін құрамыз, яғни

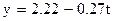болады.

Енді теориялық мәндері үшін 2013 жылға болжау төмендегідей болады:

y_t-2 = 2.22-0.27(-2) =2.76 млн м². y_t-2 = 2.22-0.27(-1) =2.49 млн м².

Эмпириялық есептелген өсіңкі қатардың мәндері, теориялық қатар мен тең деуге болады, яғни 2, 6 бағаналар.

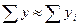
Одан әрі болжауда, сенімді аралық шекарасын қолданамыз.

Мұндағы S_y- трендтің орта квадраттық ауытқуы.t₂ – Стъюденттің t – критерийі - деңгей шамасының мәні:

Мұндағы y_i, y_t – эмпириялық, теориялық өсіңкі көрсеткіштері, n - уақыт ұзындығы, m - трендтің параметрлер саны, (m=2, сызықтың теңдеу үшін).

Кесте үшін 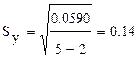млн м². Қатысты шаманың қатесі 6,32 %, (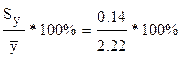). Немесе , S_у – ны табу керек?

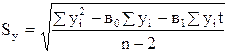, яғни: S_y=0.14млн.м².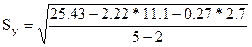

S_y = 0,14*100% = 14,0 млн. м².

Мысал-8. Өнеркәсіпте өндірілген өнім x (млн. теңге.)-мен өнімге жұмсалған шығын y (мың. теңге.) –тің арасындағы тәуелділік мына кестеде берілген.

1 2-кесте

x i
y i

- х және у арасындағы тәуелдіктің сызықтық эмпериялық байланысын есептеңіз y=a+bx ;

- екі х және у айнымалылар байланысын, тәуелдігін және 2018 жылға есептегенде шығын болжам мәні 72 млн. тенге болуы керек;

- берілген кесте мәндерін және у пен х арасындағы тәуелділікті болжап олардың графигін бейнелеңіз.

Шешуі. Келтірілген теңдеулер жүйесін құру үшін берілген 12- кестеден жолдар бойынша қосындыларды (∑) -ды есептейміз.

13- кесте

x i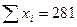
y i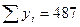
xiy i
x i ^2

13- кесте мәндерінен теңдеулер жүйесін кұрамыз.

Крамер әдісін пайдаланып Δ, Δ_a, Δ_b анықтауыштардың мәнін табамыз.

_{Δ = 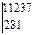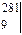=} 11237*9-281*281=22172;

Δ_{a= 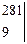=}18439*9-281*487=29104;

Δ_{b = 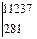=}11237*489-281*18439=291090;

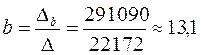
а және в коэффициенттер мәндерін теңдеуге қойып төмендегідей жазамыз.

y=1, 31x+13, 13;

y=1, 31*72+13, 13=107, 45(мың.тенге.)

y=1, 31x+13, 13  

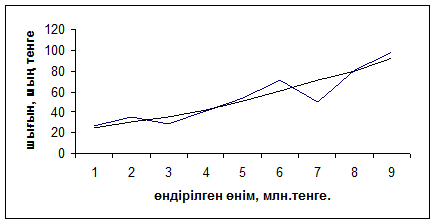
Сурет 14. Өндірілген өнімнің болжауы

Құрамында ағымды уақыттың ғана емес, сонымен қатар өткен уақыттардың айнымалыларының мәні бар модель динамикалық деп саналады. Фактор әсері үрдістің ағымды күйіне кешігіп жететін периодтар саны лаг деп аталады.

«Жұп» екі айнымалы арасындағы тәуелділікті көрсетеді. Егер бақылау нүктелері қандайда бір түзу сызықтан кездейсоқ және аздап ауытқыған болса, онда бұл 14-суретте көрсетілгендей сызықтық регрессия болып табылады.

Негізгі әдебиеттер: 3 [7-11], 6 [18-29].

Бақылау сұрақтары

1. Болжау үшін неше әдіс қолданылады:

2. Болжау әдістері не үшін қажет Халық статистикасы есептері қандай

3. Болжау әдістері қандай және қалай есептейміз

4. a және b коэффициенттер мәндерін қалай есептейміз

5.. Келтірілген теңдеулер жүйесін құру қалай құрамыз

12. Дәріс тақырыбы. Өзара тәуелділік байланысын зерттеудегі корреляциялық-регрессиялық әдісі.

Дәріс конспектілері: Статистикалық көрсеткіштердің өзара байланыс үрдісінде құбылыстардың өсіңкі факторларын талдау тек нәтижелі және факторлы көрсеткіштер арасында фукционалды байланыс болған жағдайларда қолданылады. Талдаудың бірінші кезеңіне белгілер байланысының түрін анықтау кіреді, содан кейін зерттелетін қоғамдық құбылыстың өзара байланысы үшін өсіңкі қатарларының жүйесі құрылады. Сапалы және мөлшерлі көрсеткіштердің өзара байланысы орташа деңгейлер жүйесі, өсіңкі қатарлардың құрылымдық, құбылыстардың өзгеруіне әсерін тигізеді (тұрақты және айнымалы құрылым көрсеткіштері).

Егер факторларды деп белгілесек, онда жиындық тәуелділіктің сызықтық теңдеуі келесідей болады:

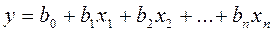(32)

Жиындық тәуелділік теңдеуінің параметрлерін есептеп, индекс мәнін келесі формуламен анықтаймыз:

(33)

мұнда 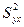– регрессия теңдеуіне қатысты есептелген эмпириалық мәнді шашыранды (ол теңдеу нәтижелі белгінің ауытқу квадраттарының қалдықты қосындысының қатынасынан анықталады), –нәтижелі белгінің эмпириалық мәндерінің шашырандысы.

Алынған теңдеу параметрлері бойынша нәтижелі көрсеткіштің деңгейінің өзгеруінде әр фактордың үлесібар екенін бағалауға болады. Ол әр факторда регрессия коэффициенттерінің шамасы бойынша тікелей бағалау арқылы немесе стандартталған меншікті регрессия коэффициенттері 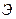икемділік коэффициенті бойынша есептелінеді.

(34)

Нәтижелі көрсеткіштің деңгейіне факторлардың әсерін, абсолютті көлем жиындық регрессия теңдеуінің коэффициенттері көрсетеді және модельге кіретін факторлардың деңгейі (орташа) белгіленген жағдайда, талданып жатқан көрсеткішке әр фактордың әсер ету дәрежесін сипаттайды. Модельденіп жатқан көрсеткіштің құрылуында әртүрлі факторлардың әсерін, бағалап салыстыру үшін, нақты шамаларды қатысты шамалармен толықтыру қажет.

Сонымен, икемділіктің жеке коэффициенттері, қалған факторлар тұрақты тіркелген жағдайда, 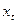белгі-факторының 1% (бір пайызға) өзгеруі -тің орташа қанша пайызға өзгеруіне әкелетінін көрсетеді.

Сәйкес 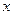факторы өзінің орташа квадраттық ауытқуының шамасына () өзгергені үшін тәуелді айнымалысының 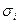орташа квадраттық ауытқуының қандай бөлігіне өзгеретінін жиындық регрессия теңдеуінің 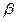-коэффициенттері көрсетеді.

Бұл коэффициент зерттеліп жатқан көрсеткіш өзгермесіне әртүрлі факторлардың әсерінің тербелісін салыстыруға мүмкіндік береді. Оның негізінде нәтижелі көрсеткіштің өзгерісі ең үлкен қорлары енген факторлар анықталады:

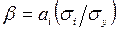(35)

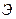– икемділік коэффициенттері келесідей өзара байланысқан:

Дата добавления: 2014-12-23