Правила построения, требования к оформлению временных диаграмм изложены в Приложении 2. 2 страница

Поставим входным сигналам в однозначное соответствие логические переменные, а выходным сигналам – функции (прописные буквы латинского алфавита). Тогда слагаемые-числа А и В можно отобразить последовательностью символов:

A 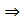<a₁a₀ > для ИМ2, A 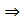< a₃a₂ a₁a₀ > для ИМ3.

B 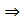<b₁b₀ > B 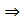< b₃b₂b₁b₀ >

Причем индекс у переменных а_i и b_i есть показатель степени 2ⁱ при определении весового коэффициента переменной в последовательности символов, отображающей число. Так что а₀ и b₀ соответствуют самым младшим разрядом слагаемых (их вес 2⁰= «1»), а переменные а₃ и b₃ – старшим разрядом с весом «8» = 2³. Аналогичный смысл имеют индексы у меток выходов и выходных функции сумматоров Si и Рi.

Рис.1 Условные графические обозначения микросхем К155ИМ2 (а) и К155ИМ3 (б)

Поэтому последовательностями

S 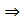< S₁S₀ > (для сумматора ИМ2) и S 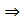< S₃S₂S₁S₀ > (для ИМ3)

Можно отобразить результат сложения. Функции Р₂ и Р₄ описывают сигналы переноса,соответственно, в третий и пятый разряды суммы (S₂ и S₄).

Зависимости выходных сигналов от входных достаточно просто отыскать по функциональной схеме сумматора. На рис.2,а приведена функциональная схема ИМС сумматора К155ИМ2. Учитывая введённые логические переменные и функции и зная реализуемые элементами И-ИЛИ-НЕ зависимости, можно записать исходные, а затем (путем преобразования по правилам и законам булевой алгебры) получить результирующие логические выражения, являющиеся логико-математической моделью этого двухразрядного сумматора:

В системе (1) использованы символы логических операций:

⊕ - сложение по модулю два (mod 2);

+ - логическое сложение (дизъюнкция); символы логического умножения пропущены (не показаны).

Из анализа выражений (1) следует, что входной сигнал переноса (p₀) влияет только на значение первого S₀ разряда суммы и входы А0, В0 и Р0 логически равнозначны, так как от перемены мест слагаемых сумма по mod 2 не меняется. Кроме того, сравнивая выражения для Р₂ и р₁, замечаем идентичность структуры из записи и отличие только в индексах у переменных а_i, b_i и p_i (i {0, 1}). Отсюда следует вывод, что двухразрядный арифметический сумматор можно рассматривать как совокупность двух одноразрядных

Рис.2 Функциональные схемы: микросхемы К155ИМ2 (а), полного одноразрядного арифметического сумматора (б) и полусумматора (в)

Сумматоров, описываемых подсистемами логических функций, соответственно:

(2) (3)

Причем выход переноса (Р₁) первого сумматора подключен к входу переноса (р₁) второго сумматора. Очевидно, этот вывод можно обобщить на случай многоразрядных сумматоров!

Системы (2) и (3) каждая описывают полный одноразрядный сумматор, функциональная эквивалентная схема которого состоит из двух логических элементов (см. рис.2,б): сумматора по mod 2 и “мажоритарного элемента» «≥2 из 3». Если в системе (2) положить р₀=0, то

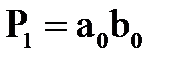и (4)

Эти выражения описывают неполный арифметический сумматор с функциональной схемой рис.2,в, называемый обычно полуссуматором.

Математическая модель (1) даёт возможность не только вычислить значения выходных сигналов в зависимости от входных, но и выяснить функциональные свойства многоразрядных полных арифметических сумматоров и, в частности, микросхемы К155ИМ2. Из выражений (4), которые являются «частным случаем» системы (1), следует, что даже полуссуматоры являются функционально полным набором логических «элементов», так как позволяют реализовать сумму по mod 2 и конъюнкцию двух сигналов.

Нетрудно придти к выводу, что микросхема К155Им3 состоит из двух двухразрядных арифметических сумматоров, и её функциональная схема содержит удвоенное количество элементов (по сравнению с рис.2,а). Функционирование сумматора ИМ3 можно описать системой логических выражений

где i ε {0,1,2,3}. (5)

ИМС арифметических сумматоров можно применять не только для сложения целых положительных чисел, но и для их вычитания. Известно, что вычитание – это сложение с отрицательным числом: А – В = А + (- В).

Однако в таком случае необходимо отображать и модуль, и знак числа. Для этого вводится дополнительный «знаковый» разряд (крайний слева в записи числа), где ставится 1, если число отрицательное, а иначе 0. Знаковый разряд участвует в сложении чисел как «обычный» (цифровой) разряд модуля числа. Но чтобы сумма была равна разности, отрицательные числа требуется представить в дополнительном коде. Дополнительный код числа – В находится по следующим правилам:

1) Число В поразрядно инвертируется, то есть единицы заменяются нулями, а нули – единицами, получим ;

2) К полученному числу прибавляется (арифметически) единица в младший разряд, затем добавляется знаковый разряд;

3) В результате получается дополнительный код:

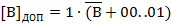
Например, В = - 0111₍₂₎ = - 7₍₁₀₎, то есть минус семь. Дополнительный код этого числа будет отображен комбинацией:

1) =1000, 2) ( +0001)=1000+0001=1001, тогда

Запомните, дополнительный код положительного числа совпадает с записью самого числа, только в знаковом разряде ставится ноль: если число А>0, то

[A]_ДОП = 0. А.

↑ - знаковый разряд

Таким образом, вычитание заменяется сложением чисел в дополнительных кодах. При этом получится дополнительный код разности. Единица переноса от сложения знаковых разрядов теряется (не учитывается), а цифра в знаковом разряде разности укажет знак результата: если 1, то разность отрицательная, а если 0, то разность – положительное число.

Пример 1.

Запишем числа А и В в дополнительных кодах

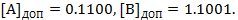
Выполним сложение

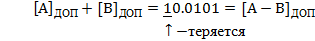
Получили результат

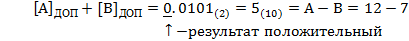
Пример 2.

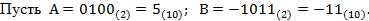
Представим эти числа в дополнительных кодах:

Выполним сложение

Чтобы найти результат в прямом коде, необходимо выполнить обратные преобразования:

1) Вычтем из полученного результата единицу

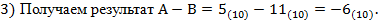
Описанный алгоритм позволяет строить на основе ИМС К155ИМ2 или …. ИМ3 «вычитатели» двоичных чисел, дополняя их схемами формирования дополнительных кодов слагаемых (по входам) и схемами преобразования дополнительного кода суммы-разности в прямой код (на выходах сумматора) [7]. По такому принципу строятся арифметические устройства микро – ЭВМ микропроцессоров, позволяющие выполнять не только сложение/вычитание, но и умножение/деление двоичных чисел.

Следует заметить, поскольку ИМС арифметических сумматоров образуют функционально полный набор, то их можно использовать для реализации любых логических функций и устройств. Однако такое применение будет оправданным, если привёдет к сокращению количества микросхем в реализуемом устройстве.

3. Описание лабораторной установки

Работа выполняется на субблоке «СУММАТОР», позволяющем исследовать 4-разрядный сумматор К155ИМ3 в статическом и динамическом режимах работы.

В статическом режиме оба слагаемых А и В можно установить «вручную» по желанию исследователя на сколь угодно большой интервал времени и любой из них изменить в любой момент времени.

В динамическом режиме значение числа А формируется автоматически непрерывно в пределах 0, 1, …14, 15 как последовательность 4-разрядный двоичных чисел. Слагаемое В задаётся фиксировано с помощью набора тумблеров. Частота смены значений слагаемого А равна ≈ 6 Гц и определяется вспомогательным генератором тактовых импульсов.

Упрощенная функциональная схема субблока приведена на рис.3, а также на его лицевой панели.

Режим работы субблока выбирается тумблером SA6, положения которого маркированы гравировкой «НЕПР» (непрерывно) и «ОДИН» (одиночно). Положение НЕПР соответствует динамическому режиму, когда состояние счётчика D3 (К155ИЕ5) непрерывно меняется под действием тактовых импульсов генератора Г1. Этот счётчик формирует слагаемое А.

Рис.3 Упрощенная функциональная схема субблока СУММАТОР

Слагаемое В формируется тумблерами SA2, … SA5 с гравировкой «В0», «В1», «В2» и «В3», соответственно.

Входной сигнал переноса имитируется тумблером SA1, имеющим гравировку «ПЕРЕНОС». Положения названных тумблеров помечены значениями «1» и «0» в соответствии со значениями сигналов.

Когда тумблер SA6 стоит в положении «ОДИН», то состояние счётчика можно изменить нажатием кнопки SB1 «ВВОД». Тогда слагаемое А увеличивается на единиц. Кнопкой SB2 «УСТ.0» (установка ноль) счётчик обнуляется и слагаемое А принимает значение 0.

Значения выходных сигналов сумматора (D4) и счётчика D3 можно проконтролировать по светодиодам (на рис.3 они не показаны), а значение числа В контролируется по положению тумблеров SA2, SA3, SA4, SA5.

Генераторы импульсов Г1 и Г2 выполнены на микросхеме К155ЛН1, D-триггеры – D2 К155ТМ2, а сумматор на К155ИМ3.

4. Задание на лабораторную работу

4.1. Уяснить состав субблока, выяснить назначение каждого элемента функциональной его схемы и расположение на лицевой панели тумблеров, кнопок и светодиодов.

4.2. Изучить принцип действия и функциональные возможности полных арифметических сумматоров и полусумматоров. Сделать выводы по функциональным свойствам микросхем К155ИМ2 и К155ИМ3.

4.3. Исследовать работу сумматора К155ИМ3 в статическом режиме при сложении и вычитании двоичных чисел. Сделать выводы о процедуре вычитания чисел и возможностях применения сумматоров для реализации некоторых логических операций.

4.4. Исследовать работу сумматора в динамическом режиме. Построить временные диаграммы для этого режима и сделать выводы о применении устройств на основе арифметических сумматоров. Эксперименты выполнить согласно указаниям п.6.4 (см. ниже).

5. Содержание отчёта

Отчет выполнить и оформить согласно требованиям, принятым на кафедре АиКС. В отчете привести:

5.1. Цель работы.

5.2. УГО микросхем К155ИМ2 и К155ИМ3, их цоколёвку и системы логических функций, реализуемых ими. Упрощенную функциональную схему сумматора ИМ3. Выводы о функциональных свойствах арифметических сумматоров.

5.3. Функциональную схему субблока (рис.3). Примеры на сложение и вычитание чисел, на реализацию логических функций (по заданному варианту табл.1), функциональную эквивалентную схему и схему включения ИМС К155ИМ3 для реализации функций по заданному варианту.

5.4. Временные диаграммы работы субблока в динамическом режиме по варианту согласно табл.2. Выводы о применении сумматоров в динамическом режиме работы.

6. Методические указания

6.1. Выясняя назначение функциональных элементов лабораторной установки, пользуйтесь схемой рис.3, а также схемой на лицевой панели субблока. Учтите, что D-триггеры D2 введены для устранения «дребезга» контактов кнопок SB1 и SB2. Сделайте предположение, что эти триггеры отсутствуют, а непосредственно кнопками будут подаваться сигналы. Каким недостатком будет обладать такая схема управления счётчиком?

6.2. Принцип действия и функциональные свойства сумматора К155ИМ3 следует изучить, применяя тот подход и метод анализа, которые были изложены при анализе сумматора К155ИМ2. Прежде всего, убедитесь в адекватности модели (1) функциональной схеме рис.2,а. Для этого, пользуясь схемой, запишите исходные алгебраические выражения функции S₀, S₁ и Р₂ через операции конъюнкции, дизъюнкции и инверсии над входными переменными (сигналами), а затем приведите их к виду (1). Ответьте на вопрос: «Почему (зачем) в схеме рис.2,а необходимы элементы НЕ?».

Затем по выражениям (5) составьте полную систему логических функции, описывающих сумматор ИМ3. Составьте функциональную эквивалентную схему этой микросхемы из логических элементов рис.2,б либо из УГО микросхем К155ИМ2, пометив входы и выходы соответствующими метками.

«Способность» сумматора ИМЗ к реализации некоторых логических функций (без дополнительных ИМС) выясните из анализа его логико-математической модели (полный системы функции). Для этого некоторым из переменных a_i, b_i и p₀ придать фиксированные значения 0 или 1 либо придать одинаковые значения, затем найти равносильные алгебраические выражения для выходных функции S₀, S₁, S₂, S₃ и Р₄. Установите их смысловое значение и начертите функциональную эквивалентную схему и схему включения К155ИМ3. (Например, так, как были получены выражения (4) и схемы рис.2,в). Схема включения ИМС – это УГО микросхемы с отображением способов подключения входов к шинам лог.0, лог.1 и между собой в соответствии с выбранным вариантом. Если переменная a_i =0, то вход А_i следует подключить к шине лог.0 (⊥), если a_i =1, то к шине лог.1. Если же a_i = b_j =c, либо a_i = a_j=с, то соответствующие входы А и В надо соединить вместе и образовать «новый» вход С. Рассмотрите несколько вариантов, сформулируйте выводы о возможностях ИМС К155ИМ3 и проверьте их экспериментально.

6.3. Эксперименты с сумматором в статическом режиме проведите в последовательности: «сложение» - «вычитание» - «реализация функции».

6.3.1. Сделайте несколько опытов на сложение чисел, полагая их положительными.

Проверьте работу сумматора, сопоставив результаты, отображаемые светодиодами с гравировками «1Р», «2Р», «3Р», «4Р» и «ПЕРЕНОС», с результатами сложения в двоичной и десятичной системах счисления. Сначала примите входной сигнал переноса равным нулю, а затем равным 1. Используйте для этого тумблер SA1. Уясните различия в получаемых результатах и сделайте вывод о действии сигнала по входу ПЕРЕНОС.

6.3.2. Опыты на вычитание проще выполнить, когда вычитаемое – постоянное число. Поэтому число В следует принять за вычитаемое и установить его с помощью тумблеров «В0», «В1», «В2», «В3» (см. рис.3). Тогда кнопкой ВВОД уменьшаемое число А можно выбрать по желанию и проконтролировать по светодиодам «А0», «А1», «А2» и «А3».

Так как сумматор ИМ3 4-разрядный. А вычитание сводится к сложению чисел в дополнительных кодах, то под модули чисел А, В и результата S необходимо отвести первых три разряда. Тогда четвёртые разряды (a₃, b₃ и S₃) следует считать знаковыми, и их значение укажет знак числа. Поэтому, проводя эксперименты, особое внимание обращайте на состояние светодиодов «А3», «4Р» (S₃) и положение тумблера «В3» (SA5). Если эти светодиоды горят, то число A => <a₂ a₁a₀> и S => <S₂ S₁ S₀> отрицательные и представлены в дополнительных кодах. Тогда для нахождения разности в прямом коде, необходимо выполнить обратные преобразования над [S]_доп. А так как число В – вычитаемое, то и оно должно быть представлено в дополнительном коде [В]_доп (тумблер «В3» должен стоять в положении «1»). Определите самостоятельно, в каком положении должен стоять тумблер SA1 (ПЕРЕНОС). Приведите несколько экспериментов на вычитание, полагая число А сначала положительным, а потом отрицательным. Руководствуясь правилами образования дополнительных кодов, проверьте получаемые результаты. Сделайте выводы по результатам проверок.

6.3.3. Эксперименты по реализации логических функций вначале следует провести в подтверждение тех выводов, которые были сделаны при выполнении п.4.2 задания. Порядок и содержание этих опытов выберите самостоятельно. Затем по указанию преподавателя выполните первое индивидуальное задание согласно табл.1, где приведены значения сигналов по входам сумматора К155ИМ3 (см. указания п. 6.2). Логические переменные { a, b, c, d } соответствуют изменяющимся сигналам на входах реализуемого сумматором «нового» устройства, а значения лог.1 и лог.0 – фиксированным «сигналам» на указанных входах сумматора.

6.3.4. Необходимо найти алгебраические выражения всех выходных функций (правая графа таблицы). По ним установить смысловое значение и названия логических операций и элементов, реализуемых микросхемой. Составьте схему включения ИМ3 по заданному варианту и функциональную эквивалентную схему сумматора, используя УГО «образующих» его элементов. Проведите эксперименты, изменяя значения аргументов a, b, c, d в доказательство полученных выражений.

6.4. Режим, когда одно слагаемое непрерывно меняется через фиксированный интервал времени, следует считать динамическим. В лабораторной установке последовательность смены значений слагаемого А предопределяется счётчиком D3 (см. рис.3). Цикл работы счётчика составляет 16 тактов, так как он 4-разрядный. Поэтому и длительность цикла смены значений сигналов на выходах сумматора также составит 16 тактов. На временных диаграммах следует отобразить только сигналы, меняющиеся во времени, и рассмотреть работу субблока не менее чем в течение 16 тактов. Это –сигналы: на входах A_i, выходах S_i, P₄, а также на входе +1 счетчика D3 (выход генератора Г1, см. рис.3). Сигналы же по входам В_i сумматора D4 имеют фиксированное значение (согласно индивидуальному заданию, табл.2) и их следует указать в подписи к диаграмм «При В => <…>.

Индивидуальное задание №1

Таблица 1

Вари-ант	Значения входных сигналов	Реализуемые фнкции
Р0	А3	А2	А1	А0	В3	В2	В1	В0
						а		b	c	S0= S1= S2= S3= P4=
	a					d	c		B
	c				a	d			d
	a				b				c
					a		c		b
		a			d			b

Кроме того, на диаграммах необходимо показать два варианта последовательностей входных сигналов: а) при Р₀=0 и б) Р₀=1. Выводы по применению сумматора К155ИМ3 в динамическом режиме работы сделайте, сопоставляя (по диаграмм) последовательности выходных и входных сигналов. Обратите при этом внимание на:

· Соотношение частот и скважностей выходных импульсов по отношению к входным последовательностям импульсов;

· Сдвиги по фазам выходных импульсов относительно входных;

· Логические зависимости выходных сигналов от входных.

Для доказательства верности диаграмм и логических зависимостей, следуя указаниям п.6.3.3., найдите алгебраические выражения выходных функций (см. табл.2). Так как значения аргументов р₀, b₃, b₂, b₁, b₀ фиксированы, то названные функции будут зависеть только от аргументов { a₃, a₂, a₁, a₀ }.

Критериями верности должно служить равенство значений сигнала на диаграмме его значению, вычисленному по алгебраическому выражению соответствующей функции. Эти значения должны совпадать для любого момента времени, входящего в интервал наблюдения (Т>16Δt, где Δt – длительность одного такта работы).

Временные диаграммы рекомендуется строить, руководствуясь вначале только логикой работы сумматора как арифметического устройства. Затем, после нахождения алгебраических выражений функций, проверить, совпадают ли вычисленные значения функций со значениями соответствующих выходных сигналов сумматора в текущем такте работы. В случае их различия отыскать ошибку и исправить либо диаграммы, либо алгебраические выражения.

Индивидуальное задание №2

Таблица 2

Вариант	Значения слагаемого В	Выходные функции сумматора
В3	В2	В1	В0	При Р0 =0	При Р0=1
					S0= S1= S2= S3= P4=	S0= S1= S2= S3= P4=

Чтобы верно сделать выводы по применению сумматоров в цифровых устройствах, проанализируйте временные диаграммы: сопоставьте последовательности входных и выходных сигналов. При этом сопоставление необходимо выполнить по частоте следования импульсов и по фазе импульсов выходной последовательности по отношению к импульсам входной последовательности.

Учтите, что сравнивать по фазе можно только последовательности импульсов одинаковой частоты! А фаза – это временной интервал между фронтом (спадом) импульса одной последовательности и фронтом (спадом) импульса другой последовательности. Для оценки величины фазового сдвига (фазового угла) принято использовать «электрические градусы». Известно, что период следования импульсов эквивалентен 360° (электрическим градусам). С другой стороны, период следования импульсов можно выразить количеством тактов и определить «долю градусов», приходящихся на один такт (Δt). Например, период следования импульсов на выходе «8» счётчика D3 (см. рис.3), то есть сигнала, соответствующего четвёртому разряду слагаемого А, равен 16 Δt. Тогда один такт будет соответствовать Δt≡360°/16 = 22,5° электрическим градусам. С учётом сказанного определите (по диаграммам), с какой дискретностью будет изменяться фаза последовательностей сигналов на выходах сумматора S0, S1, S2 и S3 по отношению к входным последовательностям a₀, a₁, a₂ и a₃, соответственно, если число В будет меняться в пределах от 0000₍₂₎ до 1111₍₂₎ (от 0÷15). Причем это надо определить для случаев, когда сигнал по входу Р0 сумматора постоянно равен нулю либо единице. Что касается сигнала ПЕРЕНОС (Р4) на одноимённом выходе сумматора, то ответьте на вопрос:

«В каких пределах будет меняться длительность импульса (лог.1) на этом выходе, если число В изменять от 0 до 15?» (Аналогично, при р₀=0 и р₀=1). На основе ответов на эти вопросы сделайте выводы о применении сумматоров.

Вопросы для самопроверки

1.Каково название ИМС К155ИМ2 и К155ИМ3 и каждого вывода этих микросхем? Приведите УГО этих микросхем.

2.Какими логическими функциями описывается полный арифметический сумматор двух, 4-разрядных двоичных чисел? Ответ иллюстрируйте функциями сумматора К155ИМ3.

3. Почему и зачем в схеме рис.2,а использованы элементы НЕ? Чем отличается полный арифметический сумматор от полусумматора?

4. Как построить 6-разрядный полный сумматор на микросхемах К155ИМ3 и К155ИМ2? Начертите функциональную схему.

5. Каким образом арифметический сумматор можно использовать для вычитания двоичных чисел? Ответ иллюстрируйте примерами.

6. В качестве каких логических элементов можно использовать микросхемы полных (неполных) арифметических сумматоров? Иллюстрируйте ответ схемами сумматора К155ИМ2 (К155ИМ3).

7. Как влияет сигнал по входу переноса на реализуемые сумматором функции и на работу сумматора в целом? Покажите это на примерах.

8. На каком из выходов сумматора К155ИМ3 можно получить сигнал переноса от сложения третьих разрядов слагаемых? Начертите схему включения этой микросхемы для такого варианта.

9. Каким образом ИМС К155ИМ3 можно использовать для получения импульсов с реагируемой скважностью? Что для этого дополнительно требуется и какой выход сумматора следует выбрать? Ответ подтвердите функциональной схемой и временными диаграммами.

10. Можно ли ИМС К155ИМ3 (…ИМ2) применить для получения последовательностей импульсов с регулируемым углом фазового сдвига одной последовательности относительно другой? Ответ иллюстрируйте функциональной схемой и временными диаграммами.

Работа 4. ФУНКЦИОНАЛЬНЫЕ СВОЙСТВА РЕГИСТРОВ

1. Цели лабораторной работы

Изучение функциональных свойств универсальных сдвиговых регистров и экспериментальное исследование режимов работы регистра на примере ИМС К155ИР13.

2. Основные сведения и понятия

Регистр – это микроэлектронное последовательностное логическое устройство, предназначенное для хранения и оперативного преобразования цифровой информации. Информация представляется двоичными последовательностями сигналов в виде «слов» фиксированной «длины». Каждое информационное слово отображается последовательностью (во времени либо в пространстве) символов 0 и 1. Число символов (разрядов) в слове называется его длиной. Обычно информационные слова имеют длину, кратную 4 битам: 4, 8, 16 и т.д. Если последовательность отображается в пространстве, то слово называют параллельным, если – во времени, то последовательным. Для передачи параллельного слова требуется соответствующее число электрических линий связи. Последовательное же слово можно передать по одной двухпроводной линии. Таким образом параллельное информационное слово представляется набором позиционных сигналов с уровнями лог. 0 и лог. 1, каждый из которых передается по отдельной (проводной) линии связи. А последовательное слово – наличием или отсутствием импульса на соответствующей временной позиции. При этом число временных позиций, отводимых под информационное слово, должно быть равно длине этого слова.

Дата добавления: 2014-12-26