Нормальный закон распределения 1 страница

Нормальный закон распределения часто называют законом Гаусса. Этот закон играет важную роль и наиболее часто используется на практике по сравнению с другими законами распределения.

Основная особенность этого закона состоит в том, что он является предельным законом, к которому приближаются другие законы распределения. В теории надежности его используют для описания постепенных отказов, когда распределение времени безотказной работы в начале имеет низкую плотность, затем максимальную и далее плотность снижается.

Распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие, примерно равнозначные факторы.

Нормальный закон распределения описывается плотностью вероятности

где: е = 2,71828 — основание натурального логарифма; π= 3,14159; т и σ -параметры распределения, определяемые по результатам испытаний.

Колоколообразная кривая плотности распределения приведена на рис. 4.2.

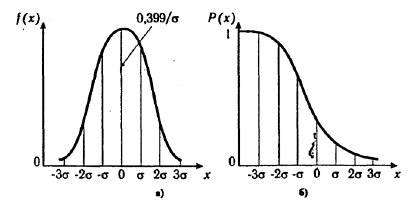
Рис. 4.2. Кривые плотности вероятности (а) и функции надежности (б)

нормального распределения

Параметр m = М_x представляет собой среднее значение случайной величины X, оцениваемое по формуле

параметр σ — среднее квадратическое отклонение случайной величины X, оцениваемое по

Интегральная функция распределения имеет вид

Вероятность отказа и вероятность безотказной работы соответственно:

Q(x) = F(x); P(x) = 1 - F(x);

Вычисление интегралов заменяют использованием таблиц нормального распределения, при котором М_х = 0 и σ = 1. Для этого распределения функции плотности вероятности имеет одну переменную t и выражается зависимостью

Величина t является центрированной (так как М_t= 0) и нормированной (так как σ_t = 1). Функция распределения соответственно запишется в виде:

Из этого уравнения следует, что F₀ (t) + F₀ (- t) = 1 или F₀ (- t) = 1 - F₀ (t).

При использовании таблицы 1 приложения следует в формулу (4.13) вместо t подставить её значение

При этом t называют квантилью нормированного нормального распределения (обычно обозначают u_p).

Плотность распределения и вероятность отказа соответственно равны f(x) = f₀(t) / σ; Q (x)=F₀ (t); тогда вероятность безотказной работы P (x) = 1- F₀ (t); где: f₀(t) F₀ (t); определяют по таблицам.

В работах по надежности часто вместо интегральной функции распределения F₀(t) ис­пользуют функцию Лапласса:

Пример 4.4. Пусть случайная величина Х представляет собой предел текучести стали. Опытные данные показывают, что предел текучести имеет нормальное распределение с па­раметрами M = 650 МПа, о = 30 МПа. Найти вероятность того, что полученная плавка стали имеет предел текучести в интервале 600 — 670 МПа.

Р е ш е н и е. Для определения вероятности воспользуемся формулой (4.17)

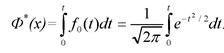(4.14)

(4.15)

Вероятности отказа и безотказной работы, выраженные через функцию Лапласса:

(4.16)

Вероятность попадания случайной величины Х в заданный интервал значений от а до в вычисляют по формуле

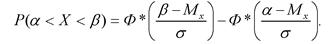(4.17)

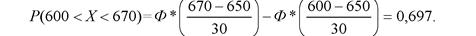
4.4. Логарифмически нормальное распределение

Логарифмически нормальное распределение нашло широкое применение в вопросах техники, биологии, экономики и теории надежности. Его успешно применяют дня описания наработки до отказа подшипников, электронных ламп и других изделий.

Неотрицательная случайная величина распределена логарифмически нормально, если ее логарифм распределен нормально. Плотность распределения для различных значений σ_х приведена на рис. 4.3.

f(x)

0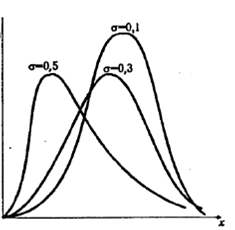

Рис. 4.3. Плотность логарифмически нормального распределения

Вероятность безотказной работы можно определить по таблицам для нормального рас­пределения (см. табл.П.1 приложения) в зависимости от значения квантили

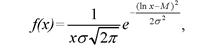(4.18)

где М и а— параметры, оцениваемые по результатам п испытаний до отказа;

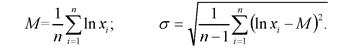(4.19)

Для логарифмически нормального закона распределения функция надежности выгля­дит так:

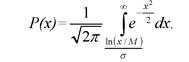(4.20)

Математическое ожидание наработки до отказа

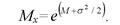(4.21)

Среднее квадратическое отклонение и коэффициент вариации соответственно равны:

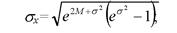(4.22)

При v_x <. 0,3 полагают, что v_x = а, при этом ошибка не более 1%.

Часто применяют запись зависимостей для логарифмически нормального закона в де­сятичных логарифмах. В соответствии с этим законом плотность распределения

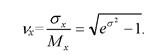(4.23)

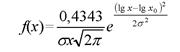(4.24)

Оценки параметров lg x₀ и σ_х определяют по результатам испытаний:

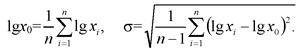(4.25)

Математическое ожидание М_х, среднее квадратическое отклонение σ_х и коэффициент вариации vx наработки до отказа соответственно равны:

(4.26)

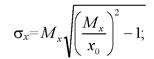(4.27)

(4.28)

4.5. Распределение Вейбулла

Закон Вейбулла представляет собой деухпараметрическое распределение. Этот закон является универсальным, так как при соответствующих значениях параметров превраща­ется в нормальное, экспоненциальное и другие виды распределений. Автор данного закона использовал его при описании экспериментально наблюдавшихся разбросов усталостной прочности стали, пределов ее упругости. Закон Вейбулла удовлетворительно описывает на­работку до отказа подшипников, элементов радиоэлектронной аппаратуры, его используют для оценки надежности деталей и узлов машин, в частности автомобилей, а также для оцен­ки надежности машин в процессе их приработки. Плотность распределения описывается за­висимостью

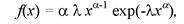(4.29)

где а — параметр формы кривой распределения; X — параметр масштаба; е =2,71828 — ос­нование натурального логарифма.

График плотности распределения дан на рис. 4.4. Функция распределения Вейбулла

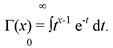
Для целочисленных значений х гамма-функцию вычисляют по формуле

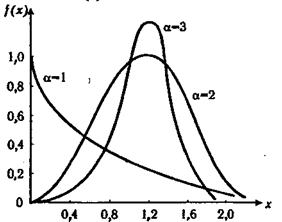
Рис. 4.4. Плотность распределения Вейбулла для X=1

Широкое применение закона распределения Вейбулла объясняется тем, что этот закон, обобщая экспоненциальное распределение, содержит дополнительный параметр а. Подбирая нужным образом параметры а и X, можно получить лучшее соответствие расчетных значе­ний опытным данным по сравнению с экспоненциальным законом, который является одно-параметрическим (параметр X).

Так, для изделий, у которых имеются скрытые дефекты, но которые длительное время не стареют, опасность отказа имеет наибольшее значение в начальный период, а потом быст­ро падает. Функция надежности для такого изделия хорошо описывается законом Вейбулла с параметром а<1.

Наоборот, если изделие хорошо контролируется при изготовлении и почти не. имеет скрытых дефектов, но подвергается быстрому старению, то функция надежности описывает­

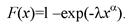(4.30)

Функция надежности для этого закона:

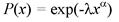(4.31)

Математическое ожидание случайной величины X равно:

(4.32)

где Г(х) — гамма-функция. Для непрерывных значений х

(4.34)

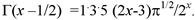(4.35)

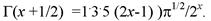(4.36)

Дисперсия случайной величины равна:

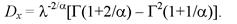(4.37)

определяется законом Вейбулла с параметром а >1. При а =3.3 распределение Вейбулла близко к нор­мальному.

4.6. Гамма-распределение.

Гамма-распределение является двухпараметрическим распределением. Оно занимает важное место в теории надежности. Плотность распределения имеет ограничение с одной стороны (0 < х < оо). Если параметр а формы кривой распределения принимает целое значе­ние, то это свидетельствует о вероятности появления такого же числа событий (например, отказов) при условии, что они независимы и появляются с постоянной интенсивностью X. Гамма-распределение широко применяют при описании появления отказов стареющих эле­ментов, времени восстановления, наработки на отказ резервированных систем. При различ­ных параметрах гамма-распределение принимает разнообразные формы, что и объясняет его широкое применение.

Плотность вероятности гамма-распределения определяется равенствами

(4.38)

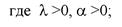
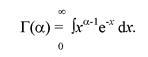(4.39)

Кривая изменения плотности распределения приведена на рис. 4.5. Функция распределения при х>0;

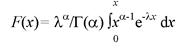(4.40)

при х < 0. F(x) = 0;

Математическое ожидание и дисперсия соответственно равны:

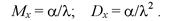(4.41)

При а <1 интенсивность отказов монотонно убывает (что соответствует периоду при­работки изделия), при а >1 — возрастает (что характерно для периода изнашивания и старе­ния элементов).

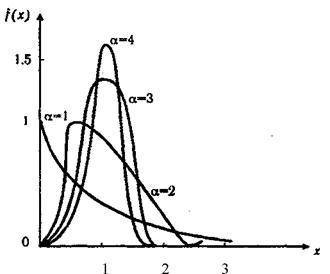
Рис. 4.5. Кривые плотности гамма-распределения

При а =1 гамма-распределение совпадает с экспоненциальным распределением, при а >10 гамма-распределение приближается к нормальному закону. Если а принимает значения произвольных целых положительных чисел, то такое гамма-распределение называют рас­пределением Эрланга. Если X =1/2, а значение а кратно 1/2, то гамма-распределение совпада­ет с распределением х² (хи-квадрат).

4.7. Установление функции распределения показателей надежности по данным статистической информации

Наиболее полной характеристикой надежности сложной системы является закон рас­пределения, выраженный в виде функции распределения, плотности распределения или функции надежности. О виде теоретической функции распределения можно судить по эм­пирической функции распределения (рис. 4.6), которая определяется из соотношения

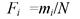(4.42)

где m_t - число отказов на интервале t; N — объем испытаний; t < t < t_i+₁ - интервал времени, на котором определяют эмпирическую функцию.

Построение эмпирической функции осуществляют, суммируя приращения, полученные на каждом интервале:

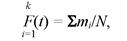(4.43)

где к - число интервалов.

Эмпирическая функция надежности является функцией, противоположной функции распределения; ее определяют по формуле

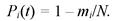(4.44)

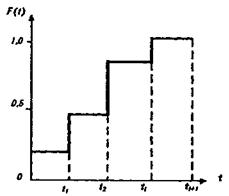
Рис. 4.6. Эмпирическая функция распределения

Оценку плотности вероятности находят по гистограмме. Построение гистограммы сводится к следующему. Всю область значений времени t разбивают на интервалы t₁, t₂,..., t_t и для каждого из этих интервалов определяют оценку плотности вероятности по формуле

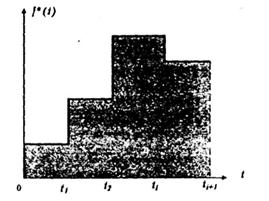
Рис. 4.7. Гистограмма.

Сглаживая ступенчатую гистограмму плавной кривой, можно по ее виду судить о зако­не распределения случайной величины. В практике для сглаживания кривой чаще всего ис­пользуют метод наименьших квадратов. Для более точного установления закона рас­пределения необходимо, чтобы число интервалов было не менее пяти, а число реализаций, попадающих в каждый интервал, - не менее десяти.

Графическое определение вида функции состоит в нанесении полученных эксперимен­тальных данных на вероятностную бумагу, представляющую собой лист бумаги, на котором в прямоугольной системе координат нанесена сетка, при этом по оси ординат - шкала, соот­ветствующая функции закона распределения (например, нормального, логарифмически-нормального и т. д.), а по оси абсцисс - линейная или логарифмическая шкала. Основная идея графического метода построения - подбор такой непрерывной замены координат, при кото­рой график функции распределения становится прямой линией. Если такую замену перемен­ных удалось отыскать, то на плоскости координат любая функция распределения этого се­мейства будет прямой линией (рис. 4.8)

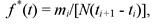(4.45)

где m_i - число отказов на i-м интервале; (t_i+₁ - t_t) - отрезок времени i -го интервала; N — объ­ем испытаний; i = 1,2,..., к - число интервалов.

Графически гистограмма может иметь вид, изображенный на рис. 4.7.

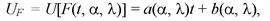(4.46)

где F(t, а, X) - функция распределения, содержащая два неизвестных параметра.

Вероятностная бумага может быть использована не только для определения вида рас­пределения, но и для нахождения параметров закона распределения. Оценки параметров за­кона распределения находят по углу наклона прямой и отрезкам, которые она отсекает на осях координат, для чего решают систему уравнений:

k = а(а, X), (4.47)

c = b(a, X),

где k = tg(cp) - тангенс угла наклона прямой линии к оси абсцисс; с - длина отрезка от точки пересечения прямой с осью абсцисс до оси ординат.

Если опытные точки располагаются на вероятностной бумаге близко к прямой, то это свидетельствует о соответствии опытных данных тому закону распределения, для которого построена вероятностная бумага.

Для нормального закона распределения справедливо следующее уравнение прямой:

(4.48)

где µ и σ - параметры распределения.

При построении вероятностной бумаги для этого распределения на горизонтальной оси откладывают равномерную шкалу для t, а на вертикальной оси - значения U_f и надписывают величину F(t), поэтому шкала на вертикальной оси получается неравномерной. Область из­менения t определяется разностью:

(3.49)

Если за ширину графика принять величину L [мм], то откладываемые на горизонталь­ной оси значения t рассчитывают с помощью соотношения

St = Kt t, (4.50)

где

Kt = L/At. (4.51)

Для построения шкалы функции распределения F(t) задаются ее минимальным [Fmin(t)] и максимальным [F_max(t)] значениями, например F_min(t) = 0,001, F_max(t) = 0,999. Тогда для U_f наименьшее значение будет U(F_min) = -3,09, а наибольшее U(F_max) = 3,09. Поэтому уравнение для SF при длине шкалы L = 300 мм записывают в следующем виде:

Sf = (U f/6,18)300 = 48,5 Uf. (4.52)

Из уравнения (3.48) следует, что при F(t) = 0,5, U_f = 0, а при F(t) <0,5 используют со­отношение

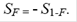. (4.53)

На рис. 4.8 дан график функции распределения на вероятностной бумаге. Прямая пере­секает ось t в точке µ (это следует из уравнения (4.48)).

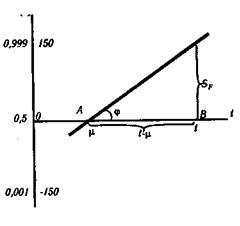
Рис. 4.8. График функции нормального распределения на вероятностной бумаге

Для определения параметра σ воспользуемся уравнениями (4.48), (4.50) и (4.52). Из этих уравнений следует

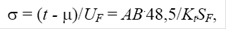(4.54)

где АВ - длина отрезка, равная t - µ, мм.

Из уравнения (4.54) и в соответствии с рис. 3.8 получим

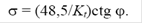(4.55)

Значение K_t известно, а ctg φ находят по графику.

При построении вероятностной бумаги для экспоненциального закона преобразуем уравнение функции распределения

F(t) = 1-ехр(-Х t) (4.56)

к линейному виду

- ln[1 - F(t)] = X t. (4.57)

Вероятностную бумагу для экспоненциального распределения (рис.4.9) строят сле­дующим образом: на горизонтальной оси откладывают равномерную шкалу для t, на верти­кальной оси - значения, определяемые по формуле (4.57), и надписывается F(t). Наименьшее значение F_min(t) = 0, наибольшее примем равным F_max(t) = 0,999. Тогда для - ln[1 - F(t)] по­лучаем наибольшее значение 6,908. Поэтому уравнение для S_F запишем в таком виде

S_F = -300 ln[1 - F(t)]/6,908 = - 43,4 ln[1 - F(t)]. (4.58)

Параметр X находим по уравнению

X = -ln[1 - F(t)]/t = SfK/(43,4 St) = (Kt/43,4)tg ф. (4.59)

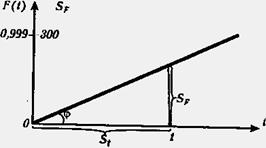
Рис. 4.9. Функция экспоненциального распределения на вероятностной бумаге

При построении вероятностной бумаги для закона распределения Вейбулла (рис.3.10) функция

F(t) = 1 - ехр(- Х^а О (4.60)

преобразуется к линейному виду

y = ln{ln[1- F(t)]} = а ln(X t) = 2,303 а|Т§ t - lg(1/X)]. (4.61)

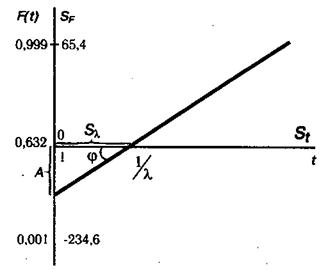
Рис. 4.10. График функции распределения Вейбулла на вероятностной бумаге

На горизонтальной оси откладывают логарифмическую шкалу в соответствии с урав­нением

S = K lg t, (4.62)

где K_t - масштабный фактор.

На вертикальной оси откладывают значения y, а надписывают величину F(t). Примем для F(t) крайние значения: 0,001 и 0,999. Для этих значений y_min = -6,91 и у_тах =1,93, т.е. раз­мах величины у равен 8,84. Поэтому уравнение для S_F имеет вид

S_F = 300 y/8,84 = 33,94 y. (4.63)

Следует подчеркнуть, что при F(t) < 0,6321 имеем S_F < 0 и при F(t) > 0,6321 имеем S_F > 0.

Из уравнения (4.63) следует, что у = 0 при t = 1/X. Поэтому значение 1/X находят в точке пересечения графика с осью t.

Параметр а находят при решении уравнения

а = Kt tg ф/78,16. (4.64)

При построении вероятностной бумаги для других законов распределения используют изложенный выше метод.

5. Причины потери работоспособности технического объекта

5.1. Источники и причины изменения начальных параметров

технической системы

Те изменения, которые происходят с течением времени в любой технической системе и приводят к потере ее работоспособности, связаны с внешними и внутренними воздействия­ми, которым она подвергается. В процессе эксплуатации на систему действуют все виды энергии, что может привести к изменению параметров отдельных элементов, механизмов и системы в целом. При этом имеется три основных источника воздействий:

- действие энергии окружающей среды, включая человека, исполняющего функции оператора или ремонтника;

- внутренние источники энергии, связанные как с рабочими процессами, протекающи­ми в технической системе, так и с работой отдельных элементов системы;

- потенциальная энергия, которая накоплена в материалах и деталях узлов системы в процессе их изготовления (внутренние напряжения в отливке, монтажные напряжения).

При работе технического объекта наблюдаются следующие основные виды энергии, влияющие на его работоспособность.

Механическая энергия, которая не только передается по всем элементам системы в про­цессе работы, но и воздействует на нее в виде статических или динамических нагрузок от взаимодействия с внешней средой.

Силы, возникающие в узлах технической системы, определяются характером рабочего процесса, инерцией перемещающихся частей, трением в кинематических парах. Эти силы являются случайными функциями времени. Природа их возникновения, как правило, связана со сложными физическими явлениями.

Механическая энергия в системе может возникнуть и как следствие тех затрат энергии, которые имели место при изготовлении отдельных частей системы и сохранились в них в по­тенциальной форме. Например, деформация частей при перераспределении внутренних на­пряжений, изменение объема детали после ее термической обработки происходят без всяких внешних воздействий.

Тепловая энергия действует на систему и ее части при колебаниях температуры окру­жающей среды, при осуществлении рабочего процесса (особенно сильные тепловые воздей­ствия имеют место при работе двигателей и ряда технологических каждого из приборов соответст­венно равна P1(t)=0,95; P2(t)=0,99; P3(t)=0,98; P4(t)=0,90; P5(t)=0,93. Найти надежность уст­ройства за время работы t.

Р е ш е н и е. Введем обозначения вероятностей безотказной работы первого - пятого приборов: А1 - А5.

Имеем: А = А₁А₂А₃А₄А₅.

По формуле умножения для независимых событий (4.26) получим:

Р(А)=Р(А_Х) Р(А₂) Р(А3) Р(А) Р(А5)=0,95*0,99*0,98*0,90*0,93=0,76.

Пример 4.10. Производят три выстрела по одной и той же мишени. Вероятность попа­дания при первом - третьем выстрелах соответственно равна: Р₁ = 0,8; Р₂ = 0,6; Р₃ = 0,3; Най­ти вероятность того, что в результате этих трех выстрелов в мишени будет хотя бы одна про­боина.

Р е ш е н и е. Рассмотрим событие В - хотя бы одно попадание в мишень. Представим событие В в виде суммы несовместных вариантов:

B=A₁A₂A₃ + A₁A₂A₃ + A₁A₂A₃ + A₁A₂A₃ + машин, при работе при­водных механизмов, электротехнических и гидравлических устройств.

Химическая энергия также оказывает влияние на работу системы. Даже воздух, кото­рый содержит влагу и агрессивные составляющие, может вызвать коррозию отдельных узлов системы.

Если же оборудование системы работает в условиях агрессивных сред (оборудование химической промышленности, суда, многие машины текстильной промышленности и др.), то химические воздействия вызывают процессы, приводящие к разрушению отдельных эле­ментов и узлов системы.

Ядерная (атомная) энергия, выделяющаяся в процессе превращения атомных ядер, может воздействовать на материалы (особенно в космосе), изменяя их свойства.

Электромагнитная энергия в виде радиоволн (электромагнитных колебаний) пронизы­вает все пространство вокруг объекта и может оказать влияние на работу электронной аппа­ратуры.

Биологические факторы также могут влиять на работоспособность системы. Например, в тропических странах имеются микроорганизмы, которые не только разрушают некоторые виды пластмасс, но даже могут воздействовать на металл.

Таким образом, все виды энергии действуют на техническую систему и ее механизмы, вызывают в ней целый ряд нежелательных процессов, создают условия для ухудшения ее технических характеристик.

5.2. Процессы, снижающие работоспособность системы

Различные виды энергии, действуя на систему, вызывают в ее узлах и деталях процес­сы, снижающие начальные параметры изделия. Эти процессы связаны, как правило, со сложными физико-химическими явлениями и приводят к деформации, износу, поломке, кор­розии и другим видам повреждений. Это, в свою очередь, влечет за собой изменение выход­ных параметров изделия, что может привести к отказу.

Приведем примеры данных взаимосвязей. Механическая энергия, действующая в звеньях металлорежущего станка, приводит к возникновению процесса износа его звеньев. Это вызывает искажение начальной формы сопряжении (т. е. их повреждение), что приводит к потере станком точности, которая является основным выходным параметром станка. При достижении определенной погрешности обработки возникает отказ.

Химическая энергия вызывает процессы коррозии в резервуарах и трубопроводах агре­гатов химической промышленности. Повреждение стенок резервуаров может привести вна­чале к ухудшению выходных параметров агрегата (загрязнение химических веществ, изме­нение пропускных сечений трубопроводов), а затем при разрушении стенок к полному выхо­ду из строя изделия.

Сочетание механических воздействий в том числе высокочастотных колебаний, а также влияние температурных и химических факторов на элементы конструкции самолетов приво­дит к тому, что в них могут возникнуть усталостные разрушения (трещины). Они снижают несущую способность системы, что при определенной величине повреждения приводит к разрушению элемента конструкции и может закончиться аврией.

Процесс, возникающий в результате действия того или иного вида энергии, может не сразу привести к повреждению изделия. Часто существует период «накопления воздействий» прежде чем начнется период внешнего проявления процесса, т. е. повреждение изделия. На­пример, для начала развития усталостной трещины необходимо определенное число циклов переменных напряжений.

Повреждение материала изделия — это отклонение его контролируемых свойств от начальных, оно связано с выходными параметрами изделия определенной зависимостью. Не всякое повреждение влияет на выходные параметры изделия. Также и определенная степень этого повреждения может не повлиять на показатели работоспособности.

В надежности машин часто пользуются понятием дефекта, т. е. такого состояния изде­лия, при котором оно не соответствует хотя бы одному из требований технической докумен­тации, однако остается работоспособным. При этом дефект рассматривается как возможная причина отказа. Понятие дефекта следует относить только к результату технологического процесса, а понятие повреждения - к результату воздействий на систему при ее эксплуата­ции. При этом необходимо рассматривать не только факт возникновения повреждений, но и оценить степень этого повреждения. При достижении некоторого максимального значения степени повреждения наступает отказ изделия.

5.3. Физика отказов

5.3.1. Анализ закономерностей изменения свойств материалов

Дата добавления: 2014-12-26