Нормальный закон распределения 4 страница

Соотношение (7.14) можно выразить через коэффициент безопасности и коэффициенты вариации, разделив числитель и знаменатель дроби на Yq,:

up = (n - 1)/(п²Уп² + Vy²)^1/2 (7.15)

где n = Y/Y Vп = с>п/^ср, Vy = aY/Y^.

В общем случае параметр Y может быть выражен функциональной зависимостью

Y = ф (Х1, X2,..., Xn) (7.16)

где x₁, x₂,..., x_n — случайные факторы.

Среднее значение Yq, и среднее квадратичесхое отклонение a _Y параметра Y как извест­ной функции случайных аргументов определяют по следующей зависимости:

^Yср = ^ф(x1ср^{, x}2ср^{,..., x}nср^{) (7.17)}

где дф/дx_i - частная производная функции ф по фактору x_i, в которую подставляют средние значения факторов x^, x_2ср, x^j,; a₁, a₂, с_п - средние квадратические отклонения фак­торов.

7.6. Проектный расчет надежности технической системы

Известно, что техническая система, как правило, состоит из большого числа подсистем, которые между собой имеют определенную взаимную связь. Приступая к расчету надежно­сти системы, предварительно устанавливают последовательность включения отдельных под­систем, а затем составляют функциональную схему работы системы во времени при выпол­нении поставленной задачи.

Надежность системы рассчитывают в каждом интервале времени, в котором задейство­ваны определенные подсистемы, при этом суммарное время работы системы будет соответ­ствовать времени выполнения поставленной задачи. Не исключено, что отдельные подсисте­мы могут работать в течение всего периода времени выполнения поставленной перед систе­мой задачи. В этом случае вероятность безотказной работы системы в течение всего времен­ного интервала определяется выражением вида

P(t) = p^h) р2^2)... р„(^),

где t_1; t^..., ty, - интервалы времени, соответствующие вероятностямp_2,...,p_n.

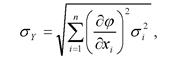
Для определения вероятностей pi(h), p₂(t₂)... p_n(t_n) для каждого интервала времени ра­боты системы составляют структурные схемы надежности. Расчет надежности на этапе про­ектирования проводят по справочным данным интенсивностей отказов элементов или ис­пользуют статистические данные, полученные по результатам испытаний или эксплуатации элементов-аналогов в составе системы.

Порядок расчета надежности по справочным данным сводится к следующему.

В зависимости от заданных условий эксплуатации системы (температуры, влажности, нагрузки и др.) взятые из справочников по надежности значения интенсивностей отказов ум­ножают на коэффициент условий применения К_у, который может быть больше или меньше единицы. Необходимо помнить, что справочные данные по интенсивностям отказов приво­дятся в основном для элементов электроавтоматики, так как эти элементы стандартизованы и выпускаются предприятиями промышленности с использованием примерно одной техноло­гии, а следовательно, и интенсивности их отказов мало отличаются.

Таким образом, чтобы установить интенсивность отказов элементов электроавтомати­ки, необходимо выполнить следующие этапы:

1) составить перечень элементов, указывая их название, а также число элементов, вхо­дящих в состав системы;

2) определить по справочнику интенсивности отказов;

3) найти коэффициенты условий применения К_у с помощью соответствующего расчета или графика по справочнику, учитывая нагрузку, температуру и др.;

4) перемножить интенсивности отказов на множители К_у. Это и будет интенсивность отказов при использовании элемента в данных условиях.

Такую же процедуру осуществляют для всех элементов системы.

Для проведения расчета составляют таблицу справочных данных, примером которой является табл. 7.1.

Таблица 7.1

Справочные данные для расчета надежности системы

Название и обо­значение элемен­та	Интенсивность отказов Ы0^6, ч^-1	Коэффициент условий приме­нения Ку	Число п эле­ментов в сис­теме	Суммарная ин­тенсивность отка­зов n Ку Ы0^6, ч^-1
Диод 2Д 106 Реле РЭС47 Датчик темпера­туры ТС-37	208,0 43,5 60,8	1,5 1,2 1,0		3120,0 261,0 121,6

Так как в процессе эксплуатации элементы системы находятся как в рабочем состоя­нии, так и в состоянии хранения и транспортирования, то используют следующие формулы пересчета интенсивностей отказов:

Хх = А-10^-3; Х = 1,5А; Ат,х = 1,5 А*. (7.18)

При показательном законе распределения времени безотказной работы надежность элемента определяется из соотношения вида

p,(t) = exp(-X t+Хт ^+Хх fx) (7.19)

При (-Х; t+AjT £т+А_гх t_x) << 1

Pi(t) * t+A* U+Ax tx) (7.20)

Если в системе предусмотрены различные виды резервирования, то при расчете надеж­ности используют соответствующие формулы.

Для восстанавливаемых систем одним из основных показателей надежности является коэффициент готовности. Расчет коэффициента и его среднего квадратического отклонения проводят по формулам:

К =1- Кр - Крег, (7.30)

где К_р - коэффициент ремонта системы:

Приближенное значение среднего квадратического отклонения

OP(t) = (h + К + А,*) = - 1n P(t)/t. (7.21) Тогда вероятность безотказной работы и среднее квадратическое отклонение системы, состоящей из последовательно соединенных элементов, определяют соответственно по фор­мулам:

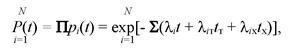
(7.22)

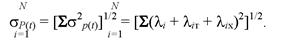
(7.23)

При расчете надежности механических, гидравлических и пневматических элементов и узлов чаще всего используют статистические данные по испытаниям или эксплуатации эле­ментов-аналогов. При наличии статистических данных вероятность безотказной работы эле­мента вычисляют по формуле

P/(t) = 1 - m,/n,, (7.24)

где t - время одного цикла испытаний (работы); m_t и n - соответственно число отказов и объем испытаний z'-го элемента. В случае, если m_t = 0, то

P/(t) = 1 - 1/[2(n + 2)]. (7.25) Среднее квадратическое отклонение элемента определяют с помощью соотношений:

OP(t) = {P/(t)[1 -P,(t)]/(n, - 1)}^1/2 при m, * 0; (7.26)

OP(t) = [1/2(n, + 2)][(5n + 7)/(n, + 3)]^1/2 при т_г = 0. (7.27)

Вероятность безотказной работы и среднее квадратическое отклонение для системы, состоящей из последовательно соединенных элементов, вычисляют соответственно по фор­мулам:

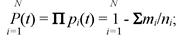
(7.28)

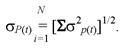
(7.29)

(7.31)

здесь К_р - коэффициент ремонта i-го элемента:

К,р = Т_ф/ Г_г-э, (7.32) где Тр - среднее время непланового ремонта /-го элемента за период его эксплуатации Г_гэ:

Тр = Т/в q, S/, (7.33)

здесь Т_/в - среднее время восстановления одного отказа; q, - вероятность отказа /-го элемента за время ^ одного цикла работы; Sj - число циклов работы /-го элемента:

Si = TJh. (7.34)

Формулы (7.32) - (7.34) справедливы для элементов, которые не контролируются в про­цессе их работы.

Для непрерывно контролируемых элементов коэффициент ремонта определяют по формуле

Кр = 7у(Тв + Ti), (7.35) где Т - среднее значение наработки на отказ i-го элемента.

Среднее квадратическое отклонение коэффициента ремонта

(7.36)

где акр ~ Кр;

а коэффициент регламента - по формуле

Крег = Трег/Тэ, (7.37)

где Т_рег — время, затраченное на проведение регламента за период эксплуатации Т_э.

Пример 7.3. В соответствии с техническим заданием разработана конструкторская до­кументация на изделие типа подвижной установки. Выполнить расчет вероятности безотказ­ной работы и коэффициента готовности, а также найти их средние квадратические отклоне­ния при следующих исходных данных: t =6 ч - время работы в течение суток (принимается пятидневная рабочая неделя); Т_рег =240 ч - время регламента (технического обслуживания), предусмотренное после каждого года эксплуатации (Т_э =8760 ч).

Для удобства используем сокращения: ц. - цикл; от. - отказ.

Решение. По результатам анализа конструкторской документации установлено, что все элементы и узлы подвижной установки при выполнении ею работы функционируют в тече­ние 6 ч в сутки. Составим структурную схему надежности изделия (рис. 7.7.).

Рис. 7.7. Структурная схема надежности изделия

Для расчета надежности элементов 1-3 структурной схемы используем статистические данные, полученные при испытаниях, а расчет надежности элемента 4 проводим по справоч­ным данным.

Расчет надежности элемента 1. В соответствии с данными, полученными при экс­плуатации металлоконструкций аналогичных изделий, предположим, что т₁ =5 от.; п₁ =5000 ц.; ^ =6 ч (длительность одного цикла работы) и t_1l5 =20 ч (среднее время восстановления од­ного отказа). Далее, подставляя исходные данные в формулы (7.24) и (7.26), определим p₁(t)

и Cp1(t):

p1(t) = 1 - т_х/щ = 1 - 5/5000 = 0,999; Cp1(t) = Wt)[1 -МОИп - 1)}^1/2 = [0,9990,001/(5000 - 1)]^1/2 = 0,004/ Для вычисления коэффициента ремонта и его среднего квадратического отклонения используем соотношения:

К1Р = Пр/Гь = m1 hJ(n\ tц) = 5^.20/(5000^.6) = 0,0033; Ок1р = = 0,0033.

Расчет надежности элемента 2. По результатам эксплуатации механических узлов аналогичных изделий имеем: т₂ =8 от.; п₂ =4000 ц.; ^ =6 ч и t_2l5 =10 ч.

Подставляя исходные данные в известные формулы, получим:

p₂(t) = 1 - m₂/n₂ = 1 - 8/4000 = 0,998;

<Jp2(0 = {p2(t)[1 -p2(t)]/(n2 - 1)}^1/2 = [0,9980,002/(4000 - 1)]^1/2 = 0,006;

К2Р = Т2р/Г2э = m2 t2в/(n2 tц) = 8'10/(60006) = 0,0033;

Ок2р = К2р = 0,0033.

Расчет надежности элемента 3. По результатам эксплуатации гидравлических узлов аналогичных изделий имеем: т₃ =15 от.; п₃ =3000 ц.; ^ =6 ч; t_3l5 =6 ч.

Подстановка исходных данных в известные формулы позволяет рассчитать:

p3(t) = 1 - m3/n3 = 1 - 15/3000 = 0,995;

<Jp3(0 = {p3(t)[1 -p3(t)]/(n3 - 1)}^1/2 = [0,9950,005/(3000 - 1)]^1/2 = 0,001; К3Р = Т3р/Г3э = m3 tзв/(nз Q = 15^.6/(3000^.6) = 0,005; Ок3р = К3р = 0,005.

Расчет надежности элемента 4. Структурная схема надежности электроавтоматики (рис. 7.8) представляет собой смешанное соединение элементов.

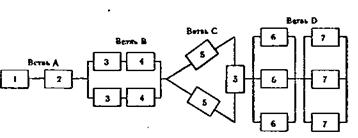
Рис. 7.8. Структурная схема надежности электроавтоматики

Составим таблицу исходных данных интенсивностей отказов (табл. 7.2.).

Для расчета надежности элемента 4 представим структурную схему в виде четырех ветвей А, В, С и D и определим надежность каждой ветви.

Таблица 7.2

Исходные данные для расчета надежности

Название элемента на схеме	Интенсив­ность отка­зов Х 10^6, ч^-1	Коэффици­ент условий применения Ку	Число n элементов в системе	Суммарная ин­тенсивность отказов пКуХ10^6, ч^-1
1.Резистор 2.Электромагнит 3. Диод 2Д106А 4. Диод 2Д106А 5. Реле РЭС 4 6 Контактор 7.Датчик температу­ры ТС-37	87,0 173,7 208,0 208,0 43,4 870,0 608,0	1,0 1,5 1,5 1,5 1,2 1,0 1,0		435,00 2605,50 312,00 312,00 52,08 870,00 608,00

Ветвь А.

Ра(0 = exp[- I(V+ ^)] = 1 - 2(V+ ^х) = 1 - [(435 + 2605,5)6 + +(435 + 2605,5) 18 10^-3] 10^-6 = 1 - (0,018 + 0,000054) = 0,98; Op_a (t) = 1р + К = - ln PA(t)/t = - ln 0,98/6 = 0,0202/6 = 0,0033. где Х_р - интенсивность отказов при работе; Х_х - интенсивность отказов при хранении. Ветвь В (поканальное резервирование). Для расчета используем формулы: Рв(0 = 1 - [1 - p(t)]² = 1 - (1 - 0,9963)² = 0,99999;

p(t) = exp[-Ј(V+ ЗД] ~ 1 - 2(V+ ~ 1 - [(312+312)6 + (312+312)1810^-3]10^-6 «1 -

(0,0037+0,000011) «0,9963;

Op_b (t) = - ln PB(t)/t = 0,00005/6 = 0,000008. Ветвь С (схема два из трех). При расчете используем формулу для схемы два из трех: Pc(t) = p³(t) + 3 p²(t)q(t) = 0,9997³ + 30,9997²0,0003 = 0,9999; p(t) = exp[- (^t+ Xхtх)] = exp[-(52,086 + 52,08 10^-3 18) 10^-6] = 0,9997; op _с (t) = - ln Pc(t)/t = 0,0001/6 = 0,00001. Ветвь D (поэлементное резервирование). При расчете воспользуемся формулой (7.12): PD(t) = {1 - [1 - p6(t)]³}{1 - [1 - p7(t)]³} = (1 - 0,125 10^-6)(1 - 0,06410^-6) =

= 0,999999;

p6(t) = exp[- (V+^х)] = 1 - (V+^х) = 1 - (8706+870 10^-3 18) 10^-6 = 0,995; p7(t) = exp[- (V+^х)] = 1 - (V+^х) = 1 - (6086+608 10^-3 18) 10^-6 = 0,996; Op_d (t) = - ln P_D(t)/t = 0,000001/6 = 0,01610^-6. Надежность электроавтоматики равна:

p4(t) = PA(t) PB(t) PC(t) PD(t) = 0,98^.0,99999^.0,9999^.0,999999 = 0,979;

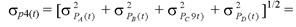
= [(3,310 "y + (0,810 "y + (110 у + (0,01610 "уу «0,0033. Из практики известно, что среднее время восстановления электроавтоматики 7_4в =5 ч. Используя формулу (7.35), вычислим коэффициент ремонта

^4р = Пв/(Г4в + T4) = 5/(5 + 153,8) = 0,031, где 1/T4 = - ln P4(t)/t = - ln 0,979/6 = 0,021/6 = 0,0065 1/ч; 74 = 1/0,0065 = 153,8 ч.

Вероятность безотказной работы и среднее квадратическое отклонение изделия в целом соответственно равны:

P(t) = p1(t) p2(t) p3(t) p4(t) = 0,9990,9980,9950,979 = 0,971;

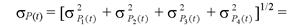
= (0,004² + 0,006² + 0,001² + 0,0033²)^1/2 = 0,008. По формуле (7.31) найдем коэффициент ремонта изделия

#р = Е&р = 0,0033 + 0,0033 + 0,005 + 0,031 = 0,0426; по формуле (7.36) - среднее квадратическое отклонение

Далее по формуле (7.37) вычислим коэффициент регламента

К_рег = 7_рег/7_э = 240/8760 = 0,027.

Из соотношения (7.30) определим коэффициент готовности

Кг = 1 - Кр - Крег = 1 - 0,0426 - 0,027 = 0,93.

Среднее квадратическое отклонение коэффициента готовности принимаем равным среднему квадратическому отклонению коэффициента ремонта:

окг = окр = 0,037.

Ответ: P(t) = 0,971; о_до = 0,008; Кг = 0,93; окг = 0,037.

7.7. Применение теории надежности для оценки безопасности

технических систем

Обеспечение безопасности машин и конструкций - составная часть проблемы надеж­ности. Под безопасностью понимаем надежность по отношению к жизни и здоровью людей, состоянию окружающей среды.

Вероятностно-статистические методы и теория надежности начали широко использо­ваться при расчете особо ответственных объектов, при анализе крупных аварий.

Основным базовым показателем надежности и безопасности технических систем может служить вероятность безотказной работы Р({) - вероятность проведения производственных процессов без происшествий в течение некоторого времени t, т. е. того, что в заданном интер­вале времени t = Т не возникнет отказа этого объекта.

Значение Р^), как всякой вероятности, может находиться в пределах 0< Р({) <1. Веро­ятность безотказной работы Р({) и вероятность отказа R(t) образуют полную группу событий, поэтому

Р(0) + R(t) = 1. (7.38)

Допустимое значение Р{() выбирается в зависимости от степени опасности отказа объ­екта. Например, для ответственных изделий авиационной техники допустимые значения Р(0)=0,9999 и выше, т.е. практически равны единице.

При высоких требованиях к надежности объекта задаются допустимым значением Р(0) = у% (у% - вероятность безотказной работы объекта в %) и определяют время работы объекта t = Т_у, соответствующее данной регламентированной вероятности безотказной работы. Зна­чение Т_у называется «гамма-процентным ресурсом» и по его значению судят о большей или меньшей безотказности и безопасности объектов.

Пусть R(t) - вероятность возникновения аварийной ситуации на отрезке времени [0, t]. Эта вероятность должна удовлетворять условию

R (Т*) < R*, (7.39)

где R* - предельно допустимое (нормативное) значение риска возникновения аварийной си­туации.

Используем нормативное значение вероятности безотказной, т. е. безопасной, работы Р*, которая весьма близка к единице (например, Р* = 1).

Функция риска на отрезке времени [0, t] дополняет функцию безопасности P(t) до еди­ницы:

R(t)=1 - P(t). (7.40)

Интенсивность риска аварийной ситуации (удельный риск) аналогична интенсивности отказов:

r(t) = -P (t)/P(t) = R(t)/[1 -R(t)]. (7.41) Поскольку уровень безопасности должен быть высоким, то можно принять 1 - R(t) = P(t) «1. (7.42) Тогда интенсивность риска аварийной ситуации будет

r(t) *R(t) = -P'(t); R(t) = dR/dt. (7.43)

Поскольку время t при оценке риска аварии исчисляют в годах, то r(t) имеет смысл го­дового риска возникновения аварийной ситуации.

Средний годовой риск аварии:

Гср(Т) = R(t)/T. (7.44)

Пусть, например, г_ср = const = 10^-5 год^-1; Т = 50 лет.

Тогда

R(7) = Гср(Т)Т = 10^-5-50 = 510^-4; P(T) = 1 - R(T) = 1- 5 10^-4 = 0,9995. Такие показатели риска аварийной ситуации широко используют в гражданской авиа­ции, а в последние годы их начали применять при нормировании безопасности оборудования атомных электростанций.

Для парка одинаковых технических объектов функция безопасности:

Pn(t) = Pⁿ(t), (7.45)

где n - численность парка одинаковых объектов.

В этом случае функция риска

Rn (t) = 1 - [1 - R(t)]ⁿ «n-R(t) (7.46)

при условии nR (t) << 1.

Аналогично для удельного риска:

Tn (t) «n r(t) и Гп.ср «n rср(t). (7.47)

Инженерные расчеты инженерных конструкций на безопасность основаны на концеп­ции коэффициентов запаса.

В этом случае расчетное условие имеет вид

F < S/m, (7.48) где F - параметр воздействия; S - параметр сопротивления; m - коэффициент безопасности (m >1).

7.8. Показатели безопасности систем «человек - машина» (СЧМ)

Надежность характеризует безошибочность (правильность) решения стоящих перед СЧМ задач. Оценивается вероятностью правильного решения задач, которая, по статистиче­ским данным, определяется соотношением

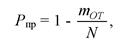(7.49)

где т_от и N - соответственно число ошибочно решенных и общее число решаемых задач.

Точность работы оператора - степень отклонения некоторого параметра, измеряемого, устанавливаемого или регулируемого оператором, от своего истинного, заданного, или но­минального значения. Количественно точность работы оператора оценивается величиной по­грешности, с которой оператор измеряет, устанавливает или регулирует данный параметр:

Y= 1н - 1оп, (7.50)

где 1_н - истинное или номинальное значения параметра; 1_оп - фактически измеряемое или ре­гулируемое оператором значение этого параметра.

Не всякая погрешность является ошибкой, до тех пор, пока величина погрешности не выходит за допустимые пределы.

В работе оператора следует различать случайную и систематическую погрешности. Случайная погрешность оператора оценивается величиной среднеквадратической погрешно­сти, систематическая погрешность - величиной математического ожидания отдельных по­грешностей.

Своевременность решения задачи СЧМ оценивается вероятностью того, что стоящая перед СЧМ задача будет решена за время, не превышающее допустимое:

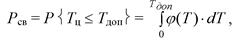(7.51)

где <р (Т) - функция плотности времени решения задачи системой «человек-машина». Эта вероятность по статистическим данным

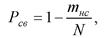(7.52)

где т_нс - число несвоевременно решенных СЧМ задач.

В качестве общего показателя надежности используется вероятность правильного (Р_пр) и своевременного (Р_св) решения задачи:

^Рсчм ^Рпр ' ^Рсв^{. (7.53)}

Безопасность труда человека в СЧМ оценивается вероятностью безопасной работы:

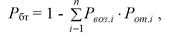(7.54)

где Р_возл - вероятность возникновения опасной или вредной для человека производственной ситуации t-го типа; Р_от; - вероятность неправильных действий оператора в t-й ситуации; - число возможных травмоопасных ситуаций.

Степень автоматизации СЧМ характеризует относительное количество информации, перерабатываемой автоматическими устройствами:

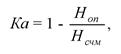(7.55)

где Н_оп - количество информации, перерабатываемой оператором; Н_счм - общее количество информации, циркулирующей в системе «человек-машина».

Экономический показатель характеризует полные затраты на систему «человек-машина». В общем случае эти затраты складываются из затрат на создание (изготовление) системы С_и, затрат на подготовку операторов С_оп и эксплуатационных расходов С_э:

Жсчм = Ен (Си + Соп)+Сэ, (7.56)

где Е_н - нормативный коэффициент экономической эффективности капитальных затрат (С_и + Соп).

Эргономические показатели учитывают совокупность специфических свойств СЧМ и представляют иерархическую структуру, включающую в себя ценностную эргономическую характеристику (эргономичность СЧМ), комплексные (управляемость, обслуживаемость, ос-вояемость и обитаемость СЧМ), групповые (социально-психологические, психологические, физиологические, антропометрические, гигиенические) и единичные показатели.

Надежность оператора - свойство качественно выполнять трудовую деятельность в те­чение, определенного времени при заданных условиях.

Ошибками оператора являются: невыполнение требуемого или выполнение лишнего (несанкционированного) действия, нарушение последовательности выполнения действий, неправильное или несвоевременное выполнение требуемого действия.

В зависимости от последствий ошибки могут быть аварийными и неаварийными.

Надежность оператора характеризуется показателями безошибочности, готовности, восстанавливаемости и своевременности.

Показателем безошибочности является вероятность безошибочной работы. Для типо­вых, часто повторяющихся операций в качестве показателя безошибочности может исполь­зоваться интенсивность ошибок

(7.57)

где Pj - вероятность безошибочного выполнения операций j-го типа; Aj - интенсивность ошибок j-го вида; Nj, nj - общее число выполненных операций j-го вида и допущенное при этом число ошибок; Tj - среднее время выполнения операций j-го вида.

Для участка устойчивой работоспособности оператора можно найти вероятность без­ошибочного выполнения операций:

9(7.58)

где kj - число выполненных операций j-го вида; r - число различных типов операций (j = 1, 2,... r).

Коэффициент готовности оператора представляет собой вероятность включения опера­тора в работу в любой произвольный момент времени:

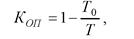(7.59)

где Т₀ - время, в течение которого оператор по тем или иным причинам не находится на ра­бочем месте; Т - общее время работы оператора.

Показатель восстанавливаемости - возможность самоконтроля оператором своих дей­ствий и исправления допущенных ошибок, т.е. представляет вероятностьисправления опера­тором допущенной ошибки:

Рисп = Рк • Роб • Ри, (7.60)

где Р_к - вероятность выдачи сигнала системой контроля; Р_об - вероятность обнаружения опе­ратором сигнала контроля; Ри - вероятность исправления ошибочных действий при повтор­ном выполнении операций.

Основным показателем своевременности является вероятность выполнения задачи в течение времени т< t„:

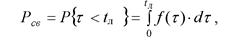(7.61)

где _Дг) - функция распределения времени решения задачи оператором.

Надежность деятельности оператора не остается величиной постоянной, а меняется с течением времени. Это обусловлено как изменением условий деятельности, так и колеба­ниями состояния оператора.

Среднее значение вероятности безошибочной работы оператора

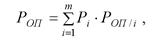(7.62)

где P_i - вероятность наступления i-го состояния СЧМ; Р_оп/; - условная вероятность безоши­бочной работы оператора в i-м состоянии; т - число рассматриваемых состояний СЧМ.

Для систем непрерывного типа показателем надежности является вероятность безот­казного, безошибочного и своевременного протекания производственного процесса в тече­ние времени t:

Рч.мл^) = Рт(t) + [1 - Рт(Фал [Реп • Рсв+(1 - Реп)Рисп)], (7.63)

где Р_т (t) - вероятность безотказной работы технических средств; К_оп - коэффициент готов­ности оператора; Р_СВ - вероятность своевременного выполнения оператором требуемых дей­ствий; Р_исп - вероятность исправления ошибочных действий.

Для СЧМ дискретного типа:

^Рч.м.2 = ^Кг ' ^рт ' ^Реп^Рсв + ^{(1 - р}т ' ^Кг)^Рвес ' ^Реп ' ^рсв + ^{(1 - Р}еп ^)рт ' ^рисп ^{. (7.64)}

где К_г - коэффициент готовности техники; Р_вос - вероятность восстановления отказавшей техники.

Вероятность Р_чм1 используется в случаях:

1) технические средства работают исправно;

2) произошел отказ технических средств, но при этом:

а) оператор безошибочно и своевременно выполнил требуемые действия по ликвида­ции аварийной обстановки;

б) оператор допустил ошибочные действия, но своевременно их исправил. Показатель надежности Р_чм2 используется, если:

1) в требуемый момент времени техника находится в исправном состоянии, не отказа­ла в течение времени выполнения задачи, действия оператора были безошибочными и свое­временными;

2) неготовая или отказавшая техника была своевременно восстановлена, операторы при решении задачи не допускали ошибок;

3) при безотказной работе техники оператор допустил ошибку, но своевременно ис­правил ее.

7.9. Роль инженерной психологии в обеспечении надежности

Конструктор, разрабатывая аппараты, отвечает да обеспечение всех требуемых харак­теристик, включая надежность. При этом разработка конструкции, выбор формы, цвета, ус­ловий эксплуатации, оптимальных условий обслуживания, управления должны вестись с учетом человеческих возможностей и ограничений.

Роль человеческого фактора в снижении надежности очень высока. Частота отказов по вине человека колеблется от 20 до 80 %:

Ps(t) = Pч(t)•Рм(t), (7.65) где P_S - показатель надежности всей системы; P,j - показатель надежности человека; Р_м -показатель надежности машины.

Надежность человека при проектировании машины должны также учитываться, как и надежность машины. Между надежностью и инженерной психологией как областями науки существует естественная связь. Обе области связаны с прогнозированием и улучшением ха­рактеристик систем, но действуют они разными способами и средствами. Специалист по на­дежности изменяет конструкцию, материал, схему, снижает нагрузки. Специалист по инже­нерной психологии воздействует на те технические факторы, которые оказывают влияние на возможности оператора: уровень шума, освещенность, уровень воздействия окружающей среды и т. д.

Дата добавления: 2014-12-26