Нормальный закон распределения 2 страница

Изменение начальных свойств и состояния материалов, из которых выполнено изделие, является первопричиной потери им работоспособности, так как эти изменения могут привес­ти к повреждению изделия и к опасности возникновения отказа.

Чем глубже изучены закономерности, описывающие процессы изменения свойств и со­стояния материалов, тем достовернее можно предсказать поведение изделия в данных усло­виях эксплуатации и обеспечить сохранение показателей надежности в требуемых пределах.

Хотя для оценки надежности, как правило, используются вероятностные характеристи­ки, это не значит, что суждение о поведении изделия можно сделать лишь на основании ста­тистических исследований.

Наоборот, в основе потери машиной работоспособности всегда лежат физические зако­номерности, но в силу разнообразия и переменности действующих факторов эти зависимо­сти приобретают вероятностный характер.

Пусть скорость некоторого процесса повреждения материала у есть функция ряда входных параметров Z₁, Z₂,..., Z_n и времени t, причем данная зависимость получена на основе физико-химических законов:

у = dU/dt = ф (Z1, Z2,..., Zn, t) (5.1)

Параметры Z характеризуют условия эксплуатации (нагрузки, скорости, температура и др.), состояние материала (твердость, прочность, качество поверхности и т. д.) и другие фак­торы, влияющие на протекание процесса повреждения материала. Однако при наличии толь­ко функциональной зависимости, достаточно достоверно описывающей данное явление, нельзя еще точно предсказать, как будет протекать данный процесс, так как сами аргументы Z^... Z_n являются случайными величинами.

Действительно, при работе машины происходят непредвиденные изменения и колеба­ния нагрузок, скоростей, температур, степени загрязнения поверхностей. Более того, сами детали машины могут быть выполнены с различными допусками на технологические пара­метры (точность, однородность материала и др.).

Однако знание физической закономерности процесса в корне изменяет возможности по оценке хода процесса по сравнению со случаем, когда этот процесс оценивается только на основе статистических наблюдений.

Функциональная зависимость, хотя и абстрагирует действительность и лишь с извест­ной степенью приближения отражает физическую сущность процесса, но позволяет предска­зывать возможный ход процесса при различных ситуациях.

Поэтому «физика отказов», которая изучает закономерности изменения свойств мате­риалов в условиях их эксплуатации, является основой для изучения и оценки надежности машин.

Для решения инженерных задач надежности необходимо знать закономерности изме­нения выходных параметров системы и ее элементов во времени. Современная наука изучает закономерности изменения свойств и состояния материалов на следующих уровнях.

Субмикроскопический уровень, когда на основании рассмотрения строения атомов и молекул и образования из них кристаллических решеток твердых тел или иных структур вы­являются закономерности, которые служат базой для объяснения свойств и поведения мате­риалов в различных условиях.

Микроскопический уровень рассмотрения свойств материалов исходит из анализа про­цессов, происходящих в небольшой области. Полученные при этом закономерности в даль­нейшем распространяются на весь объем тела.

Изучение влияния совместного действия силовых и физико-химических факторов на поведение твердых тел в процессе их эксплуатации привело к появлению нового направле­ния - физико-химической механики материалов.

Макроскопический уровень рассматривает изменение начальных свойств или состояния материала всего тела (детали). Так теория упругости на основе закона Гука рассматривает деформации и напряжения в системах и деталях различной конфигурации, работающих на растяжение, кручение, изгиб и другие виды деформации.

Разнообразные закономерности и методы расчетов, применяемые при конструировании и производстве машин, полученные общие физические законы и частные зависимости могут быть использованы и при решении вопросов надежности. При этом, поскольку главной зада­чей является оценка изменения свойств и состояния материала в функции времени, необхо­димо выявить, какие физические закономерности могут быть использованы и как проявляет­ся фактор времени при оценке работоспособности изделия.

5.3.2. Законы состояния

Как физические законы, так и полученные на их основе частные зависимости, описы­вающие изменение свойств и состояния материалов, можно разделить на две основные груп­пы.

Во-первых, это закономерности, описывающие взаимосвязи обратимых процессов, ко­гда после прекращения действия внешних факторов материал (и соответственно деталь) воз­вращается в исходное состояние. Эти зависимости называются законами состояния.

Во-вторых, имеются закономерности, которые описывают необратимые процессы и, следовательно, позволяют оценить те изменения начальных свойств материалов, которые происходят или могут происходить в процессе эксплуатации изделия. Эти зависимости на­зываются законами старения.

Законы состояния можно разделить на статические, когда в функциональную зависи­мость, описывающую связь между входными и выходными параметрами, фактор времени не входит, и на переходные процессы, где учитывается изменение выходных параметров во времени.

Типичными примерами статических законов состояния могут служить закон Гука, за­кон теплового расширения твердых тел и др. На основании этих законов получены расчет­ные зависимости для решения различных инженерных задач.

Статические законы, описывающие изменения состояния изделия, хотя и не включают фактор времени, но могут быть использованы для расчетов надежности, если известны изме­нения характеристик изделия в процессе эксплуатации.

Законы состояния, описывающие переходные процессы, например колебания упругих систем, процессы теплопередачи и другие, хотя и включают фактор времени, но также не учитывают изменений, происходящих при эксплуатации изделий. Обычно они относятся к категории быстропротекающих процессов или процессов средней скорости. Лишь при из­вестном изменении уровня внешних воздействий их можно использовать для решения задач надежности.

5.3.3. Законы старения

Основное значение для оценки потери изделием работоспособности имеет изучение за­конов старения, которые раскрывают физическую сущность необратимых изменений, проис­ходящих в материалах изделия. Хотя законы старения всегда связаны с фактором времени, в некоторых из них время непосредственно не фигурирует, так как в полученных зависимостях отыскивается связь с другими факторами (например, энергией), которые, в свою очередь, проявляются во времени. Такие зависимости будем называть законами превращения.

Типичным примером законов превращения могут служить зависимости, описывающие процессы коррозии. Вывести закономерности, непосредственно отражающие изменение ве­личины коррозии во времени, трудно: во-первых, в результате поливариантности коррозий­ных процессов, когда большое число факторов оказывает одновременно и часто противопо­ложное действие на интенсивность повреждения, и во-вторых, коррозия может быть не толь­ко равномерно распределенной по поверхности металла (например, в виде окисной пленки), но и носить локальный характер (местная коррозия) или проявляться в виде межкристаллит-ной коррозии.

Для оценки возможности возникновения и интенсивности коррозионного процесса применяют законы химической термодинамики.

Применение физико-химических закономерностей для оценки интенсивности протека­ния процессов химической коррозии является типичным подходом к анализу сложных явле­ний старения и разрушения материалов.

Хотя для прогноза поведения изделия при эксплуатации и для выбора оптимальных решений желательно было бы иметь непосредственные зависимости протекания данного процесса старения во времени, сложность явления не позволяет на данном этапе получить эту закономерность.

Поэтому используются, физические и химические законы, отражающие наиболее суще­ственные стороны процесса и показатели, по которым можно косвенно судить об интенсив­ности процесса.

Законы старения, оценивающие степень повреждения материала в функции времени, являются основой для решения задач надежности. Они позволяют прогнозировать ход про­цесса старения, оценивать возможные его реализации и выявлять наиболее существенные факторы, влияющие на интенсивность процесса. Типичным примером таких зависимостей являются законы износа материалов, которые на основе раскрытия физической картины взаимодействия поверхностей дают методы для расчета интенсивности процесса изнашива­ния или величины износа в функции времени и оценивают параметры, влияющие на ход процесса.

Многие временные закономерности физико-химических процессов могут быть получе­ны на основе рассмотрения кинетики термоактивационных процессов. Изменение свойств твердых тел происходит в результате перемещений и перегруппировок элементарных частиц (атомов, молекул, электронов, протонов и др.), изменения их положения в кристаллической решетке.

Это относится к той небольшой части элементарных частиц, энергия. которых превос­ходит некоторый уровень, который называется энергией активации Е_а. Скорость данного процесса тем больше, чем большее число частиц обладает энергией выше, чем энергия акти­вации.

Любой процесс старения возникает и развивается лишь при определенных внешних ус­ловиях. Для оценки возможных видов повреждения материалов деталей машин необходимо установить область существования процесса старения и в первую очередь условия его воз­никновения. Для возникновения процесса обычно должен быть превзойден определенный уровень нагрузок, скоростей, температур или других параметров, определяющих его проте­кание. Этот начальный уровень или порог чувствительности особенно важно знать для быс-тропротекающих процессов старения, когда после возникновения процесса идет его интен­сивное лавинообразное развитие. Часто порог чувствительности связывают с некоторым энергетическим уровнем, который определяет начало данного процесса. Например, энергия активации Е_а определяет энергетический уровень, начиная с которого может идти процесс изменения свойств материала.

Энергетическая концепция лежит в основе теории возникновения трещин в металличе­ских конструкциях при средних напряжениях, остающихся ниже предела текучести.

5.4. Отказы, вызываемые общими причинами (множественные отказы)

Множественный отказ есть событие, при котором несколько элементов выходят из строя по одной и той же причине. К числу таких причин могут быть отнесены следующие:

- конструкторские недоработки оборудования (дефекты, не выявленные на стадии проектирования и приводящие к отказам вследствие взаимной зависимости между электри­ческими и механическими подсистемами или элементами избыточной системы);

- ошибки эксплуатации и технического обслуживания (неправильная регулировка или калибровка, небрежность оператора, неправильное обращение и т. я.);

- воздействие окружающей среды (пыль, грязь, температура, вибрация, а также экс­тремальные режимы нормальной эксплуатации);

- внешнее катастрофическое воздействие (естественные внешние явления, такие, как наводнение, землетрясение, пожар, ураган);

- общий изготовитель (резервируемое оборудование или его компоненты, поставляе­мые одним и тем же изготовителем, могут иметь общие конструктивные или производствен­ные дефекты. Например, производственные дефекты могут быть вызваны неправильным вы­бором материала, ошибками в схемах монтажа, некачественной пайкой и т. п.);

- общий внешний источник питания (общий источник питания для основного и резерв­ного оборудования, резервируемых подсистем или элементов);

- неправильное функционирование (неверно выбранный комплекс измерительных при­боров или неудовлетворительно спланированные меры защиты).

Известен целый ряд примеров множественных отказов атомных электростанций. Так, некоторые параллельно соединенные пружинные реле выходили из строя одновременно и их отказы были вызваны общей причиной; вследствие неправильного расцепления муфт при техническом обслуживании два клапана оказались установленными в неправильное положе­ние; из-за разрушения паропровода имели место сразу несколько отказов коммуникационно­го щита. В некоторых случаях общая причина вызывает не полный отказ резервированной системы (одновременный отказ нескольких узлов, т. е. предельный случай), а менее серьез­ное общее понижение надежности, что приводит к повышению вероятности совместного от­каза узлов системы.

6. Основные характеристики надежности элементов и систем

6.1. Показатели надежности невосстанавливаемого элемента

Невосстанавливаемым называют такой элемент, который после работы до первого от­каза заменяют на такой же элемент, так как его восстановление в условиях эксплуатации не­возможно. В качестве примеров невосстанавливаемых элементов можно назвать диоды, кон­денсаторы, триоды, микросхемы, гидроклапаны, пиропатроны и т. п.

Пусть время работы невосстанавливаемого элемента представляет собой случайную величину т. В момент времени t = 0 элемент начинает работать, а в момент t = т происходит его отказ, следовательно, т является временем жизни элемента. Таким образом, т имеет слу­чайный характер, и в качестве основного показателя надежности элемента можно назвать функцию распределения, которая выражается зависимостью вида

F(t) = P(z<t). (6.1)

Функцию F(t) называют также вероятностью отказа элемента до момента t. Если эле­мент работает в течение времени t непрерывно, то существует непрерывная плотность веро­ятности отказа

(6.2)

Следующим показателем надежности является вероятность безотказной работы за за­данное время t или функция надежности, которая является функцией, обратной функции распределения

P(t) = 1- F(t) = P (r> t). (6.3)

Графически функция надежности представляет собой монотонно убывающую кривую (рис. 6.1; при t=0 P(t =0)=l; при t -^оо P(t =оо)=0).

В общем виде вероятность безотказной работы испытуемых элементов конструкций определяется как отношение числа элементов оставшихся исправными в конце времени ис­пытания к начальному числу элементов поставленных на испытание:

P(t) = (N - n)/N, (6.4)

где N - начальное число испытуемых элементов; п - число отказавших элементов за t; N - п = n0 - число элементов, сохранивших работоспособность.

Величина P(t) и вероятность появления отказа F в момент времени t связаны соотно­шением

P(t) + F(t) = 1, (6.5)

откуда

F(t) = 1 - P(t) (6.6)

или

F(t) = 1 - n0/N. (6.7)

Производная функции (6.4) по времени имеет вид

dP(t)/dt = - (1/N) dn/dt. При dt—0, это выражение является мгновенным значением

(6.8) плотности

распределения времени безотказной работы f(t), т.е.

(1/N) dn/dt —f(t) или dP(t)/dt = - f(t) (6.9)

Учитывая, что P(t) = n₀/N выражение (6.8) можно записать в виде

dn(t)/dt = - NdP/dt = dm(t)/dt. (6.10)

Разделив обе части соотношения (6.10) на n₀(t) получим:

[1/n0(t)]dn(t)/dt = - [N/n0(t)]dP(t)/dt = Щ, (6.11)

где X(t) - интенсивность отказов.

Подставляя формулу (6.9) в соотношение (6.11) получаем выражение для мгновенного значения интенсивности отказов

Щ = - [1/P(t)] dP(t)/dt = f(t)/P(t). (6.12)

Вероятность безотказной работы из выражения (6.12) можно представить в виде

- dP(t)/P(t) = X(t)dt. (6.13)

Интегрируя обе части уравнения (6.13) по времени в интервале [0, t], получаем

(6.14)

При известных начальных условиях, т.е. при t = 0, когда P(t) = 1, это интегральное уравнение принимает вид

Рис. 6.1.Кривая функции надежности

(6.15)

Из формулы (6.15) получаем общее выражение для вероятности безотказной работы

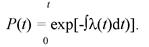(6.16)

^ нимищью дсшнши выражении мижни пилучшь фирмулу дли tscpuxittu^iM UCJUlKcWHUM

работы любого элемента технической системы при любом известном распределении времени наработки на отказ.

Важнейшим показателем невосстанавливаемого элемента является среднее время без­отказной работы (Т ₀), которое определяют как математическое ожидание случайной вели­чины

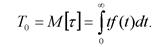(6.17)

После преобразования:

(6.18)

Среднее время безотказной работы и среднюю наработку до отказа можно получить по результатам испытаний. Для этого нужно проводить испытания до тех пор, пока не отка­жет последний из элементов. Пусть время жизни каждого из элементов соответственно рав­но т₁, т₂,..., т₃. Тогда средняя наработка до отказа

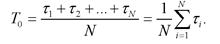(6.19)

Так как практически невозможно осуществить испытания всех элементов до отказа, то при большом значении п среднюю наработку до отказа можно определить по формуле

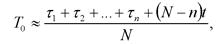(6.20)

где n — число отказавших элементов, N — число элементов, поставленных на испытания.

Пример 6.1. На испытания поставлено N =100 элементов. Испытания проводились в течение t = 200 ч. В процессе проведения испытаний отказало n = 5 элементов, при этом от­казы зафиксированы в следующие моменты: т₁ = 50 ч; т₂ = 80 ч; т₃ = 90ч; т₄ = 100 ч; т₅ = 150 ч; остальные элементы не отказали. Определить среднюю наработку до отказа Г₀.

Решение. Для решения задачи воспользуемся формулой (6.20)

70 =[(50+80+90+100+150)+(100-5)200]/100 =194,7 ч.

Ответ: Т₀ = 194,7ч.

Если испытаниям подвергают N элементов и т₁, x₂,...x_N —время их жизни, то стати­стическую дисперсию находят из выражения

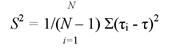(6.21)

где т = (1/N)Ex_i.

На практике в качестве оценки надежности чаще используют среднее квадратическое отклонение (о), которое определяют как корень квадратный из дисперсии:

о[т]= ф[т])^1/2. (6.22)

Одной из важнейших характеристик надежности невосстанавливаемого элемента явля­ется интенсивность отказов, или опасность отказа, которая определяет надежность эле­мента в каждый данный момент времени. Интенсивность отказа находят по формуле

= f(t)/P(t) = - [dP(t)/dt]/P(t) = - P'(t)/P(t). (6.23)

Вероятность безотказной работы в интервале (t₁, ^)выражается зависимостью

(6.24)

Функция X(t) может быть определена по результатам испытаний. Предположим, что испытаниям подвергают N элементов. Пусть n(t) — число элементов, не отказавших к мо­менту t. Тогда при достаточно малом At и достаточно большом N получим

X(t) = An/[At n(t)], (6.25)

где An — число отказов на участке At.

Статистическая интенсивность отказов X(t) равна отношению числа отказов, проис­шедших в единицу времени, к общему числу неотказавших элементов к этому моменту вре­мени.

Многочисленные опытные данные показывают, что для многих элементов функция X(t) имеет корытообразный вид (рис. 6.2).

Рис. 6.2. Кривая интенсивности отказов во времени

Анализ графика показывает, что время испытания можно условно разбить на три пе­риода. В первом из них функция X(t) имеет повышенные значения. Это период приработки или период ранних отказов для скрытых дефектов. Второй период называют периодом нор­мальной работы. Для этого периода характерна постоянная интенсивность отказов. Послед­ний, третий период — это период старения. Так как период нормальной работы является ос­новным, то в расчетах надежности принимается X(t) = X = const. В этом случае при экспонен­циальном законе распределения функция надежности имеет вид:

Р(0) = exp(- X t). (6.26)

Среднее время жизни соответственно равно:

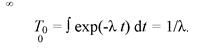(6.27)

Поэтому функцию надежности можно записать и так:

Р(0 = ехр(-#70>). (6.28)

Если время работы элемента мало по сравнению со средним временем жизни, то можно использовать приближенную формулу

Р(0) ~ 1 - t/Т₀. (6.29)

Пример 6.2. По данным эксплуатации генератора установлено, что наработка до отказа подчиняется экспоненциальному закону с параметром X = 210^-5 1/час.

Найти вероятность безотказной работы за время t = 100 часов. Определить математиче­ское ожидание наработки до отказа.

Решение.

Определим вероятность безотказной работы по формуле (6.26):

P(t) = e^{- X t} = exp(-210^-5.100) = 0,998. Математическое ожидание наработки до отказа определяем по формуле (5.27):

M0 = 1/X = 1/(210^-5) = 510⁴ ч. Ответ: P(t) = 0,998; M0 = 510⁴ ч.

Пример 6.3. Построить кривую интенсивности отказов по данным табл. 6.1. На ис­пытания поставлено N элементов (N = 200), испытания проводились в течение t = 100 ч.

Таблица 6.1.

Результаты испытаний элемента (к примеру 6.3.)

№ п/п	At, ч	An	n(t)	№ п/п	At, ч	An	n(t)
	0-10 10-20 20-30 30-40 40-50				50-60 60-70 70-80 80-90 90-100

Обозначения: At — интервал испытаний; An — число отказов; n(t) — число неотказав-ших элементов.

Для построения кривой (рис.6.3.) вычислим интенсивность отказов X(t_i) ч^-1 по формуле

(6.25):

X(t1) = 10/(10190) = 0,0052; = 8/(10182) = 0,0044;

X(t3) = 6/(10176) = 0,0034; X(t4) = 4/(10172) = 0,0023;

X(t₅) = 2/(10170) = 0,0011; X(t₆) = 2/(10168) = 0,0011;

X(t7) = 2/(10166) = 0,0012; X(t8) = 4/(10162) = 0,0024;

X(t₉) = 5/(10157) = 0,0032; X(t₁₀) = 8/(10 149) = 0,0053.

X(t)10^-3, ч^-1

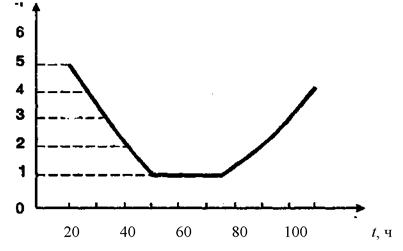
Рис. 6.3. Кривая интенсивности отказов во времени

6.2. Показатели надежности восстанавливаемого элемента

Большинство сложных технических систем с длительными сроками службы являются восстанавливаемыми, т.е. возникающие в процессе эксплуатации отказы систем устраняют при ремонте. Технически исправное состояние изделий в процессе эксплуатации поддержи­вают проведением профилактических и восстановительных работ.

Для осуществляемых в процессе эксплуатации изделий работ по поддержанию и вос­становлению их работоспособности характерны значительные затраты труда, материальных

средств и времени. Как правило, эти затраты за время эксплуатации изделия значительно превышают соответствующие затраты на его изготовление. Совокупность работ по поддер­жанию и восстановлению работоспособности и ресурса изделий подразделяют на техниче­ское обслуживание, и ремонт, которые, в свою очередь, подразделяют на профилактические работы, осуществляемые в плановом порядке и аварийные, проводимые по мере возникно­вения отказов или аварийных ситуаций.

Свойство ремонтопригодности изделий влияет на материальные затраты и длитель­ность простоев в процессе эксплуатации. Ремонтопригодность тесно связана с безотказно­стью и долговечностью изделий. Так, для изделий, с высоким уровнем безотказности, как правило, характерны низкие затраты труда и средств на поддержание их работоспособности. Показатели безотказности и ремонтопригодности изделий являются составными частями комплексных показателей, таких как коэффициенты готовности К_г. и технического обслужи­вания К_ти.

К показателям надежности, присущим только восстанавливаемым элементам, следует отнести среднюю наработку на отказ, наработку между отказами, вероятность восстановле­ния, среднее время восстановления, коэффициент готовности и коэффициент технического использования.

Средняя наработка на отказ — наработка восстанавливаемого элемента, приходящая­ся, в среднем, на один отказ в рассматриваемом интервале суммарной наработки или опреде­ленной продолжительности эксплуатации:

(6.30)

где t_; — наработка элемента до i-го отказа; m — число отказов в рассматриваемом интервале суммарной наработки.

Наработка между отказами определяется объемом работы элемента от i-го отказа до (i + 1)-го, где i =1, 2,..., m.

Среднее время восстановления одного отказа в рассматриваемом интервале суммарной наработки или определенной продолжительности эксплуатации

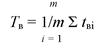(6.31)

где t_; — время восстановления i-го отказа; т — число отказов в рассматриваемом интервале суммарной наработки.

Коэффициент готовности Кг. представляет собой вероятность того, что изделие будет работоспособно в произвольный момент времени, кроме периодов выполнения планового технического обслуживания, когда применение изделия по назначению исключено. Этот по­казатель является комплексным, так как он количественно характеризует одновременно два показателя: безотказность и ремонтопригодность.

В стационарном (установившемся) режиме эксплуатации и при любом виде закона рас­пределения времени работы между отказами и времени восстановления коэффициент готов­ности определяют по формуле

Кг = Tо/(Tо + Tв) (6.32)

где T_о — средняя наработка на отказ; T_в — среднее время восстановления одного отказа.

Таким образом, анализ формулы показывает, что надежность изделия является функци­ей не только безотказности, но и ремонтопригодности. Это означает, что низкая надежность может быть несколько компенсирована улучшением ремонтопригодности. Чем выше интен­сивность восстановления, тем выше готовность изделия. Если время простоя велико, то го­товность будет низкой.

Другой важной характеристикой ремонтопригодности является коэффициент техниче­ского использования, который представляет собой отношение наработки изделия в единицах времени за некоторый период эксплуатации к сумме этой наработки и времени всех просто­ев, обусловленных устранением отказов, техническим обслуживанием и ремонтами за этот период. Коэффициент технического использования представляет собой вероятность того, что изделие будет работать в надлежащем режиме за время Т. Таким образом, К_и определяется двумя основными факторами — надежностью и ремонтопригодностью.

Коэффициент технического использования характеризует долю времени нахождения элемента в работоспособном состоянии относительно рассматриваемой продолжительности эксплуатации. Период эксплуатации, для которого определяется коэффициент технического использования, должен содержать все виды технического обслуживания и ремонтов. Коэф­фициент технического использования учитывает затраты времени на плановые и неплановые ремонты, а также регламенты, и определяется по формуле

К_та = ^Л>н + tв + tр + t₀), (6.33)

где tjj — суммарная наработка изделия в рассматриваемый промежуток времени; 4, tj, и ^ — соответственно суммарное время, затраченное на восстановление, ремонт и техническое об­служивание изделия за тот же период времени.

Пример 6.4. Определить коэффициент готовности системы, если известно, что среднее время восстановления одного отказа равно Т_в = 5 ч, а среднее значение наработки на отказ составляет Т₀ = 500 ч.

Решение. Для определения коэффициента готовности воспользуемся формулой (6.32)

Кг = T₀/(T₀ + Гв) = 500/(500 + 5) = 0,99.

Ответ: Кг = 0,99.

Пример 6.5. Определить коэффициент технического использования машины, если из­вестно, что машину эксплуатируют в течение года (Т_э = 8760 ч). За этот период эксплуатации машины суммарное время восстановления отказов составило 4 = 40 ч. Время проведения регламента составляет t<, = 20 ч. Суммарное время, затраченное на ремонтные работы за пе­риод эксплуатации составляет 15 суток, т.е. tj, = 15х24 = 360 ч.

Решение. Коэффициент технического использования вычислим по формуле (6.33), но сначала определим суммарное время наработки машины:

^ = Гэ - ^ + tр + О = 8760 - (40 + 360 + 20) = 8340 ч.

Ки = ^Л>н + tв + tр + 4) = ^/Тэ = 8340/8760 = 0,952.

Ответ: Ки = 0,952.

Пример 6.6. При эксплуатации сложной технической системы получены статистиче­ские данные, которые сведены в табл. 6.2. Определить коэффициент готовности системы.

Таблица 6.2

Статистические данные, полученные при эксплуатации сложной технической системы (к примеру 6.6)

Дата добавления: 2014-12-26