Нормальный закон распределения 3 страница

Число от-	Время, ч
Номер системы	казов mt	восстановление отказа	работы Ч	Суммарное восста­новление mltBJ
2 3	2 5		200 300
		5 2		50 30 60
Итого 70 - 4400

Наработка на отказ

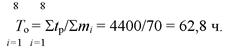
Среднее время восстановления

По формуле (6.32) по вычисленным значениям 7_о и 7_в находим коэффициент готовно­сти системы:

#_г=62,8/(62,8+2,9)=0,95

6.3. Показатели надежности системы, состоящей из независимых элементов

Всякая система характеризуется безотказностью и ремонтопригодностью. В качестве основной характеристики безотказности системы служит функция надежности, которая представляет собой вероятность безотказной работы в течение некоторого времени t.

Пусть система состоит из n элементов, функции надежности которых обозначим через p₁(t), p₂(t),.. p_n(t). Так как элементы, входящие в состав системы, являются независимыми, то вероятность безотказной работы системы определяется как произведение вероятностей со­ставляющих ее элементов

Р(0 = P1(t)P2(t)...pn(t). (6.34)

В частном случае, когда функции надежности составляющих элементов имеют экспо­ненциальное распределение с постоянными интенсивностями отказов, функция надежности системы определяется по формуле

(6.35)

Одной из важнейших характеристик безотказности системы является среднее время жизни, которое вычисляют, используя выражение

(6.36)

Для случая экспоненциального распределения среднее время жизни системы равно

(6.37)

Среднее время жизни системы или наработку на отказ по результатам статистических данных вычисляют по формуле

Т_с = 7/m, (6.38) где Т — суммарная наработка системы, полученная по результатам испытаний или эксплуа­тации; т — суммарное число отказов, зафиксированное в процессе испытаний или эксплуа­тации.

Коэффициент оперативной готовности характеризует надежность системы, необходи­мость применения которой возникает в произвольный момент времени (кроме планируемых периодов, в течение которых применение системы по назначению не предусматривается), начиная с которого система будет работать безотказно в течение заданного времени t. Значе­ние коэффициента оперативной готовности определяют из выражения

Ко = К P(t) = F(t) Tc/(Tc +Тв). (6.39)

Пример 6.6. Определить коэффициент оперативной готовности системы за период времени t = 10 ч, если известно, что система состоит из пяти элементов с соответствующи­ми интенсивностями отказов, ч-¹: Х₁ = 210^-5; Х₂ = 510^-5; Х₃ = 10^-5; Х₄ = 2010^-5; Х₅ = 5010^-5, а среднее время восстановления при отказе одного элемента равно Т_в = 10 ч. Результатами ис­пытаний установлено, что распределение наработки на отказ подчиняется экспоненциально­му закону.

Решение. Вероятность безотказной работы определим по формуле (6.35):

Р(0 = ехр[-£)ц t] ~ 1 - ()ц+Х2+Ъ+Х4+Х5)10^-5 t = =1- (2+5+1+20+50)10^-5.10 = 0,992. Значение Tc определяем по формуле (6.37)

Тс = 1/(^1 + ^2 + X? + >ч + А*) = 10⁵/78 = 1282 ч. Используя формулу (6.39), вычислим коэффициент оперативной готовности

Ko = P(t)Tc/(Tc + Тв) = 0,992 1282/(1282 + 10) = 0,984. Ответ: Ko = 0,984.

Пример 6.7. При эксплуатации в течении одного года (Т_э = 1 год = 8760 ч.) изделий специального назначения было зафиксировано пять отказов (m = 5). На восстановление каж­дого отказа в среднем затрачено двадцать часов (Т_в = 20 ч.). За указанный период экс­плуатации был проведен один регламент (техническое обслуживание). Время регламента со­ставило десять суток (Т_р = 240 ч.). Определить коэффициенты: готовности (К_г) и техниче­ского использования (К_и).

Решение. Коэффициент готовности определим по формуле

Кг = 1 - (m Тв/Тэ) = 1 - (520/8760) = 0,9886. Коэффициент технического использования равен:

Ки = 1 - (m Тв + Тр)/Тэ = 1 - (520 + 240)/8760 = 0,9612.

Ответ: Кг= 0,9886; Ки = 0,9612.

6.4. Выбор и обоснование показателей надежности технических систем

Одной из важнейших задач на этапе проектирования является правильный выбор но­менклатуры нормируемых показателей надежности. Необоснованный выбор показателей на­дежности из широкой номенклатуры имеющихся показателей может привести к неправиль­ным решениям при проектировании системы. Поэтому при выборе показателей надежности необходимо учитывать назначение системы, условия и режимы ее работы, а также ее ремон­топригодность.

Информация о назначении системы дает возможность определить область и интенсив­ность применения системы по назначению. Сведения об условиях и режимах работы систе­мы используют для оценки влияния факторов окружающей среды на работоспособность проектируемой системы, а также влияния действующих внешних и внутренних нагрузок на несущую способность элементов системы. Количественные значения этих оценок являются исходными данными для расчета прочности и устойчивости элементов и узлов металлокон­струкций.

Если по условиям применения систему предполагается ремонтировать в условиях экс­плуатации, то в качестве одного из основных показателей надежности следует выбирать ко­эффициент готовности К_г или коэффициент технического использования К_и.

В случае, если отказ системы или отдельных ее элементов приводит к невыполнению важной задачи или нарушает безопасность работы обслуживающего персонала, а также вы­зывает угрозу для здоровья и жизни людей, находящихся в зоне действия системы, то для та­ких систем основным показателем надежности является безотказность, выражающаяся в ви­де наработки на отказ или вероятности безотказной работы.

Если в результате простоя системы после отказа возникают большие материальные за­траты, то такая система должна иметь хорошую ремонтопригодность и высокие показатели безотказности.

Если система по условиям эксплуатации подлежит длительному хранению (ожиданию работы) или она должна транспортироваться на специальных транспортных средствах, то та­кая система должна обладать высокими показателями сохраняемое™ в соответствующих ус­ловиях хранения и транспортирования.

Все показатели надежности проектируемой системы должны обеспечивать нормальное ее функционирование в течение заданного срока эксплуатации.

6.5. Распределение нормируемых показателей надежности

Распределение норм надежности проводят на этапах эскизного и рабочего проектиро­вания технической системы. Предполагается, что на любом из этих этапов конструирования систему можно разбить на некоторое число подсистем в виде отдельных сборочных единиц и исходить из начальной надежности каждой подсистемы, полученной расчетом или по ре­зультатам испытаний подсистем.

Пустьр₁,р₂,...,р_п означают надежность подсистем. Предположим, что отказ любой под­системы приводит к отказу системы в целом, тогда надежность системы на основании тео­ремы умножения вероятностей имеет вид:

P = Р1 P2..-Pn. (6.40) Пусть Р^тр - требуемая надежность системы, причем значение надежности должно удов­летворять условию Р^тр > Р. Задача состоит в том, чтобы повысить хотя бы одно из значений на столько, чтобы Р > Р^тр. Для повышения надежности необходимо произвести до полни-тельные затраты, связанные либо с введением резервирования в этой системе, либо с введе­нием в систему более надежных элементов.

Методика повышения надежности Р до требуемого значения Р^тр сводится к следующе­му. Надежности р₁, р₂,..., р_п располагают в неубывающей последовательности:

Р1 < Р2 <...< Рп. (6.41) Каждую из надежностей р₁, р₂,..., р_к увеличивают до одного и того же значения р₀^тр, а надежности, начиная с р_к+₁,..., р_п, остаются неизменяемыми. Номер к выбирают из макси­мального значения j, для которого

(6.42)

j=1

где рп+1 =1 по определению.

Значение р₀^тр определяют из соотношения

(6.43)

Очевидно, что надежность системы после определения р₀^тр будет удовлетворять задан­ному требованию, поскольку новая надежность равна:

ххример о.о. пусть техническая система состоит из трех подсистем, падежнисть каж­дой из них соответственно равна: p1 =0,7; р2 =0,8; р3 =0,9. Известно, что отказ любой одной подсистемы приводит к отказу системы в целом. Требуемое значение надежности системы равно =0,65.

Провести перераспределение норм надежности таким образом, чтобы произведение ве­роятностей трех подсистем соответствовало заданному требованию.

Решение. Используя формулу (6.40), получим:

P = Р1 р2 р3 =0,70,80,9 = 0.504. Предположим, что мы не рассчитываем k по формуле (6.42), а произвольно задаем k =1. Тогда, подставляя исходные данные в формулу (6.43), получим:

Р0^тр = [0,65/0,80,91,0]^1/1 = 0.903.

P = 0,9030,80,9 = 0.65.

Полученное значение надежности соответствует требуемому Р^тр =0,65.

Однако на основании полученного значения р₀^тр можно заключить, что распределение средств, необходимых для повышения надежности, не было оптимальным. Другими слова­ми, приложено больше средств для достижения заданного показателя, чем требовалось.

Определим теперь к по формуле (6.42). С этой целью вычислим три величины:

Г1 = [Р^/Р2 Р3^.1,0]^1/1 = [0,65/0,80,91,0]^1/1 = 0,903;

Г2 = [Р^тр/р3^.1,0]^1/2 = [0,65/0,9-1,0]^1/2 = 0,85;

Г3 = [Р^тр/1,0]^1/3 = [0,65/1,0]^1/3 = 0,866.

Так как p₁<r₁, p₂<r₂, р₃ >r₃, примем к =2. В этом случае наибольшее значение индекса j со свойством p<r, равно двум. Далее, учитывая выражение (6.43), находим

р0^тр = [0,65/0,9]^1/2 = 0,85.

Это означает, что средства на повышение надежности необходимо распределить сле­дующим образом: надежность подсистемы №1 увеличивают с 0,7 до 0,85; надежность под­системы №2 - с 0,8 до 0,85; надежность подсистемы №3 оставляют на прежнем уровне. В ре­зультате вероятность безотказной работы всей системы:

Р = (0,85)²0,90 = 0,65.

7. Расчет показателей надежности технических систем

7.1. Структурные модели надежности сложных систем

Большинство технических систем являются сложными системами, состоящими из от­дельных узлов, деталей, агрегатов, систем управления и т.п. Под сложной системой пони­мается объект, предназначенный для выполнения заданных функций, который может быть расчленен на элементы (компоненты), каждый из которых также выполняет определенные функции и находится во взаимодействии с другими элементами системы.

С позиций надежности сложная система обладает как отрицательными, так и положи­тельными свойствами.

Факторы, отрицательно влияющие на надежность сложных систем, следующие:

- во-первых, это большое число элементов, отказ каждого из которых может привести к отказу всей системы;

- во-вторых, оценить работоспособность сложных систем весьма затруднительно с точ­ки зрения статистических данных, т.к. они часто являются уникальными или имеются в не­больших количествах;

- в-третьих, даже у систем одинакового предназначения каждый экземпляр имеет свои незначительные вариации свойств отдельных элементов, что сказывается на выходных па­раметрах системы. Чем сложнее система, тем большими индивидуальными особенностями она обладает.

Однако сложные системы обладают и такими свойствами, которые положительно влияют на их надежность:

- во-первых, сложным системам свойственна самоорганизация, саморегулирование или самоприспособление, когда система способна найти наиболее устойчивое для своего функционирования состояние;

- во-вторых, для сложной системы часто возможно восстановление работоспособности по частям, без прекращения ее функционирования;

- в-третьих, не все элементы системы одинаково влияют на надежность сложной сис­темы.

Анализ работоспособности сложной системы связан с изучением ее структуры и тех взаимосвязей, которые определяют ее надежное функционирование.

При анализе надежности сложных систем их разбивают на элементы (компоненты) с тем, чтобы вначале рассмотреть параметры и характеристики элементов, а затем оценить работоспособность всей системы. Под элементом можно понимать составную часть сложной системы, которая может характеризоваться самостоятельными входными и выходными па­раметрами. При исследовании надежности системы элемент не расчленяется на составные части, и показатели безотказности и долговечности относятся к элементу в целом. При этом возможно восстановление работоспособности элемента независимо от других частей и эле­ментов системы.

Анализ надежности сложных систем имеет свои специфические особенности. Влияние различных отказов и снижение работоспособности элементов системы по-разному скажутся на надежности всей системы.

При анализе надежности сложной системы все ее элементы и компоненты целесооб­разно разделить на следующие группы.

1) Элементы, отказ которых практически не влияет на работоспособность системы (деформация ограждающего кожуха машины, изменение окраски поверхности и т. п.). Отка­зы (т. е. неисправное состояние) этих элементов могут рассматриваться изолированно от сис­темы.

2) Элементы, работоспособность которых за рассматриваемый период времени прак­тически не изменяется (станины и корпусные детали, малонагруженные элементы с боль­шим запасом прочности).

3) Элементы, ремонт или регулировка которых возможна при работе изделия или во время остановок, не влияющих на его эффективность (подналадка и замена режущего инст­румента на станке, регулировка холостого хода карбюратора автомобильного двигателя).

4) Элементы, отказ которых приводит к отказам системы.

Таким образом, рассмотрению и анализу надежности подлежат лишь элементы по­следней группы. Как правило, имеется ограниченное число элементов, которые в основном и определяют надежность изделия. Эти элементы и подсистемы выявляются при рассмотре­нии структурной схемы параметрической надежности.

Модели надежности устанавливают связь между подсистемами (или элементами сис­темы) и их влиянием на работу всей системы. Структурная схема надежности определяет функциональную взаимосвязь между работой подсистем (или элементов) в определенной по­следовательности. Эту схему составляют по принципу функционального назначения соот­ветствующих подсистем (или элементов) при выполнении ими определенной части работы, выполняемой системой в целом. Техническая система может быть сконструирована таким образом, что для успешного ее функционирования необходима исправная работа всех ее элементов. В этом случае ее называют последовательной системой. Есть также системы, в которых при отказе одного элемента другой элемент способен выполнить его функции. Та­кую систему называют параллельной. Очень часто системы обладают свойствами как парал­лельных, так и последовательных систем — системы со смешанным соединением. При рас­чете надежности необходимо исследовать действия системы, основываясь на ее функцио­нальной структуре и используя вероятностные соотношения.

Такое исследование структуры позволяет выявить узкие места в конструкции системы с точки зрения ее надежности, а на этапе проектирования разработать конструктивные меры по устранению подобных узких мест. Например, можно заранее подсчитать, сколько резерв­ных элементов необходимо для обеспечения заданного уровня надежности системы. Далее можно рассчитать надежность системы, построенной из элементов с известной надежностью, или наоборот, исходя из требования к надежности системы, предъявить требования к надеж­ности элементов.

7.2. Структурная схема надежности системы с последовательным

соединением элементов

Имеются структурные схемы надежности системы с последовательным соединением элементов (рис. 6.1), когда отказ одного элемента вызывает отказ другого элемента, а затем третьего и т. д. Например, большинство приводов машин и механизмы передач подчиняются этому условию. Так, если в приводе машины выйдет из строя любая шестерня, подшипник, муфта, рычаг управления, электродвигатель, насос смазки, то весь привод перестанет функционировать. При этом отдельные элементы в этом приводе не обязательно должны быть соединены последовательно.

Такую структурную схему называют схемой с последовательным соединением зависи­мых элементов. В этом случае надежность системы определяют по теореме умножения для зависимых событий.

Рассмотрим систему, состоящую из двух или более элементов. Пусть А — событие, со­стоящее в том, что система работает безотказно. a A_i (i=l, 2,..., п) — события, состоящие в исправной работе всех ее элементов. Далее предположим, что событие А имеет место тогда и только тогда, когда имеют место все события A_i, т.е. система исправна тогда и только тогда, когда исправны все ее элементы. В этом случае систему называют последовательной систе­мой.

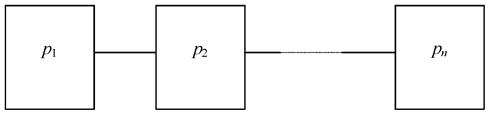
Рис.7.1. Структурная схема надежности системы с последовательным соединением

элементов

Известно, что отказ любого элемента такой системы приводят, как правило, к отказу системы. Поэтому вероятность безотказной работы системы определяют как произведение вероятностей для независимых событий.

Таким образом, надежность всей системы равна произведению надежностей подсистем или элементов:

(7.1)

Обозначив Р(А) = Р; Р(А_г) = p_i, получим

(7.2)

где Р — надежность.

Сложные системы, состоящие из элементов высокой надежности, могут обладать низ­кой надежностью за счет наличия большого числа элементов. Например, если узел состоит всего из 50 деталей, а вероятность безотказной работы каждой детали за выбранный проме­жуток времени составляет Pi = 0, 99, то вероятность безотказной работы узла будет P(t) =

(0,99)⁵⁰ = 0,55.

Если же узел с аналогичной безотказностью элементов состоит из 400 деталей, то P(t) = (0,99)⁴⁰⁰ = 0,018, т.е. узел становится практически неработоспособным.

Пример 7.1. Определить надежность автомобиля (системы) при движении на заданное расстояние, если известны надежности следующих подсистем: системы зажигания p1 = 0,99; системы питания топливом и смазкой p2 = 0,999; системы охлаждения p3 = 0,998; двигателя р4 = 0,985; ходовой части р5 = 0,997.

Решение. Известно, что отказ любой подсистемы приводит к отказу автомобиля. Для определения надежности автомобиля используем формулу (7.2)

Р = Р1Р2 Р3 Р4 P5 = 0,990,9990,9980,9850,997 = 0,979.

Ответ: Р = 0,979.

7.3. Структурные схемы надежности систем с параллельным соединением элементов

В практике проектирования сложных технических систем часто используют схемы с параллельным соединением элементов (рис. 7.2.), которые построены таким образом, что от­каз системы возможен лишь в случае, когда отказывают все ее элементы, т.е. система ис­правна, если исправен хотя бы один ее элемент. Такое соединение часто называют резерви­рованием. В большинстве случаев резервирование оправдывает себя, несмотря на увеличе­ние стоимости. Наиболее выгодным является резервирование отдельных элементов, кото­рые непосредственно влияют на выполнение основной работы. При конструировании техни­ческих систем в зависимости от выполняемой системой задачи применяют горячее или хо­лодное резервирование.

Горячее резервирование применяют тогда, когда не допускается перерыв в работе на переключение отказавшего элемента на резервный с целью выполнения задачи в установ­ленное время. Чаще всего горячему резервированию подвергают отдельные элементы. Ис­пользуют горячее резервирование элементов и подсистем, например источников питания (аккумуляторные батареи дублируются генератором и т.п.).

Холодное резервирование используют в тех случаях, когда необходимо увеличение ре­сурса работы элемента, и поэтому предусматривают время на переключение отказавшего элемента на резервный.

Существуют технические системы с частично параллельным резервированием, т. е. системы, которые оказываются работоспособными даже в случае отказа нескольких элемен­тов.

Рис. 7.2. Структурная схема надежности системы с параллельным соединением элементов

Рассмотрим систему, имеющую ряд параллельных элементов с надежностью p(t) и со­ответственно ненадежностью q(t) = 1- p(t). В случае, если система содержит п элементов, ко­торые соединены параллельно, вероятность отказа системы равна:

Q = [q(t)]ⁿ, (7.3)

а вероятность безотказной работы

P(t) = 1- [q(t)]ⁿ. (7.4)

При частично параллельном резервировании вероятность безотказной работы системы, состоящей из общего числа элементов n, определяют по формуле:

(7.5)

где p(t) — вероятность безотказной работы одного элемента; j — число исправных элементов, при котором обеспечивается работоспособность системы; С_п^к = n!/[k!(n - k)!] - число сочета­ний из n элементов по k.

В случае j =1 система будет полностью параллельной, в остальных случаях - частично параллельной.

7.4. Структурные схемы надежности систем с другими видами

соединения элементов

Следует отметить, что в практике проектирования технических систем часто использу­ют структурные схемы надежности с параллельно-последовательным соединением элемен­тов. Так, например, часто при проектировании систем с радиоэлектронными элементами применяют схемы, работающие по принципу два из трех, когда работоспособность обеспе­чивается благодаря исправному состоянию любых двух элементов. Надежность такой схемы соединения определяют по формуле

P(t) = p³(t) +3p²(t)q(t). (7.6)

где p(t) — надежность каждого элемента за время работы t одинакова; q(t)=1- p(t).

Широкое применение в проектировании нашли так называемые мостиковые схемы. Надежность такой схемы определяют из соотношения вида

P(t) = p⁵(t) + 5p⁴(t) q(t) + 8p³(t) q²(t) + 2p²(t) q³(t). (7.7)

Здесь все элементы также имеют одинаковую надежность.

Различают структурные схемы надежности с поканальным и поэлементным резервиро­ванием.

Структурная схема надежности с поканальным резервированием показана на рис. 6.3.

Рис. 7.3. Структурная схема надежности с поканальным резервированием Формула надежности выглядит так:

P = pn pri'p1n)(1-p21p22^..p2n)(1-pk1pk2^.pnk)] (7.8)

^При Pi j=Pj

P = ppfpnf (7.9) Если p_ij = р, то

P = l- (l - pⁿ)^k (7.10)

В практике проектирования часто используют структурную схему надежности с поэле­ментным резервированием (рис. 6.4).

Рис. 7.5. Структурная схема надежности технической системы

Решение. При расчете надежности воспользуемся формулами как для последовательно­го, так и для параллельного соединения элементов:

Р = PlP2[l- (l-P3P4)(l-P5P6)][l" (l-P7)(l-P8)(l-P9)] =

Рис.7.4. Структурная схема надежности с поэлементным резервированием Надежность такой системы определяют по формуле:

P = [1 - (1-рц)(1 - P21)...(l - Pk1)][l - (1 - P12)(1-P22)...(l - P*2)]^...[1- (1-Pm)(1-P2n)...(1-Pkn)]. (7.11)

P = [1 - (1 - P1)^k][1- (1 - P2)^k]-[1- (1 - Pn)^k]. (7.12)

Если = P, то

P = [1 - (1 - P)^k]ⁿ. (7.13)

Анализ последних двух схем показывает, что структурная схема с поэлементным ре­зервированием имеет более высокую надежность по сравнению с поканальным резервирова­нием.

Пример 7.2. Техническая система предназначена для выполнения некоторой задачи. С целью обеспечения работоспособности система спроектирована со смешанным соединением элементов (рис. 7.5.).

Определить надежность системы, если известно, что надежность ее элементов равна:

P1=0,99; P2=0,98; P3=0,9; P4=0,95; P5=0,9; P6=0,9; P7=0,8; P8=0,75; P9=0,7.

P1= 0,990,98[1- (1- 0,90,95)(1- 0,90,9)][1- (1- 0,8)(1- 0,75)(1- 0,7)] = 0,927.

При расчете схемной надежности данную систему представляют в виде структурной схемы, в которой элементы, отказ которых приводит к отказу всей системы, изображаются последовательно, а резервные элементы или цепи - параллельно. Следует иметь в виду, что конструктивное оформление элементов, их последовательное или параллельное соединение в конструкции еще не означает аналогичного изображения в структурной схеме надежности.

Разницу между конструктивной (монтажной) и структурной схемами можно показать на примере работы двух фильтров гидросистемы, которые для повышения надежности рабо­ты системы могут быть установлены (рис.7.6) последовательно или параллельно.

Отказ фильтра может произойти в результате двух основных причин - засорения сетки и ее разрыва.

В случае засорения сетки структурная схема надежности соответствует конструктив­ной. Последовательное соединение фильтров в этом случае только снизит надежность систе­мы, так как отказ любого из фильтров приведет к отказу системы, поскольку необходимый поток жидкости не будет проходить сквозь фильтр.

Рис.7.6. Конструктивные и структурные схемы надежности соединения фильтров при раз­личных видах отказов

При отказе фильтра из-за разрыва сетки структурная схема надежности противополож­на конструктивной. При параллельном конструктивном выполнении отказ любого фильтра будет означать отказ системы, так как при разрыве сетки поток жидкости пойдет через дан­ный фильтр и не будет происходить ее фильтрация. Поэтому структурная схема надежности изображена в виде последовательных элементов. При последовательном конструктивном включении фильтров, наоборот, разрыв сетки одного из них не будет означать отказа, по­скольку дублирующий фильтр продолжает выполнять свои функции. Поэтому структурная схема надежности изображена в виде параллельного соединения.

7.5. Зависимости для расчета вероятности безотказной работы

по заданному критерию

Работоспособность механических узлов и металлоконструкций характеризуется рядом критериев (параметров) — прочностью, износостойкостью, жесткостью, устойчивостью, точностью и др. Расчет надежности основывается на сравнении расчетного значения заданного критерия с его предельным значением, выбираемым по нормативным или справочным данным или устанавливаемым при испытаниях или наблюдениях в эксплуатации.

Работоспособность деталей или узлов оценивают по заданному критерию, если расчет­ное его значение Y меньше предельного У_п. В общем случае значение Y не должно превы­шать предельного значения. Таким образом, для обеспечения работоспособности заранее за­дают коэффициент безопасности n = YJY. Расчетные параметры рассматривают как детер­минированные величины, хотя в действительности они имеют рассеяние. Поэтому расчет проводят по наиболее неблагоприятным значениям параметров, при этом истинное значение коэффициента безопасности остается неизвестным.

С переходом на вероятностные методы расчета параметры Y и Y_Il рассматривают как случайные величины, и вероятность безотказной работы Р по заданному критерию опреде­ляют по табл. П.1 приложения в зависимости от квантили:

up = (Гп_Хр - Гср)/(ап² + Qy²)^1/2 (7.14) где u_p — квантиль нормированного нормального распределения; Yq, и Y^q, - средние значе­ния величин Y и Yu; <с_п и a_Y - средние квадратические отклонения величин Yu и Y.

Дата добавления: 2014-12-26