
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Шушляков Д. А. 1 страница
|
|
|
|
Харьков – ХНУМГ – 2014
КОНСПЕКТ ЛЕКЦИЙ
ШУШЛЯКОВ Д.А.
ГОРОДСКОГО ХОЗЯЙСТВА имени А.Н. БЕКЕТОВА
ТЕХНИЧЕСКАЯ МЕХАНИКА ЖИДКОСТЕЙ И ГАЗОВ
для студентов специальностей по направлению подготовки
6.060101 «Строительство» и 6.170202 "Охрана труда"
высших учебных заведений
УДК 533.6 (075)
ББК 22.253.3я7
Ш 98
Автор:
Шушляков Д. А. к.т.н., доц. кафедры теплохолодоснабжения (Харьковский национальный университет городского хозяйства имени А.Н. Бекетова)
Ш 98 Техническая механика жидкостей и газов: консп. лекций / Д.А. Шушляков; Харьк. нац. унив. гор. хоз-ва
им. А. Н. Бекетова. – Х: ХНУГХ, 2014. – 83 с.
В рассматриваются основные физические свойства, законы равновесия и движения жидкостей и газов, применительно к технике, инженерным сетям и безопасности жизнедеятельности.
Предназначен для студентов специальностей по направлению
подготовки 6.060101 «Строительство» и 6.170202 "Охрана труда".
| Рис. 34 | Табл. 7 | Библ. 7 |
УДК 533.6 (075)
ББК 22.253.3я7
| © Д.А. Шушляков, 2014 | |
| © ХНУГХ им. А. Н. Бекетова, 2014 |
Оглавление
1. Предмет технической механики жидкости и газов 4
2. Основные физические свойства жидкости 4
2.1. Плотность жидкости. Вязкость жидкостей. Капиллярные явления. Аномальные жидкости. Идеальная жидкость 4
3. Равновесие капельных жидкостей 18
3.1. Равновесное состояние жидкости и действующие силы 18
3.2. Гидростатическое давление в точке 20
3.3. Общие дифференциальные уравнения равновесия жидкости 23
3.4. Равновесие капельной жидкости в поле земного тяготения 29
3.5. Абсолютное и избыточное давление. Вакуум 32
3.6. Давление жидкости на плоские стенки. Центр давления 33
3.7. Давление жидкости на криволинейные поверхности. Закон Архимеда 36
4. Уравнение энергии и теорема импульсов 42
4.1. Основные понятия и определения движения жидкости 42
4.2. Уравнение Бернулли для элементарной струйки несжимаемой жидкости 48
4.3. Уравнение неразрывности 55
5. Общие сведения о гидравлических сопротивлениях 59
5.1. Виды гидравлических сопротивлений 59
5.2. Общая формула для потерь напора на трение при равномерном движении жидкости в трубах 62
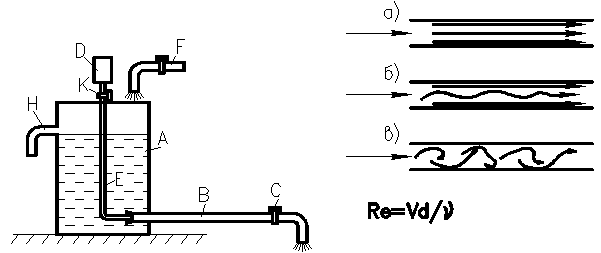
5.3. Ламинарное и турбулентное движение жидкости 65
5.4. Число Рейнольдса 66
5.5. Особенности ламинарного и турбулентного движения жидкости в трубах 69
5.6. Потери напора на трение в круглой трубе 72
5.7. Опытные данные о распределении скоростей и потерях напора 74
5.8. Местные гидравлические сопротивления. Общие сведения 77
6. Задачи 80
Список литературы 82
1. Предмет технической механики жидкости и газов
Механика жидкости и газов – наука, рассматривающая основные законы движения и равновесия жидкостей (как капельных, так и газообразных), а также их силовое взаимодействие с твердыми телами.
Механику жидкости можно разделить на две части:
1) теоретическая механика жидкости, где излагаются основные положения теории равновесия и движения капельных жидкостей и газов;
2) прикладная (техническая) механика жидкости, в которой рассматривается приложение этих законов к ряду практических случаев.
Знание механики жидкости необходимо для решения целого ряда инженерных задач – расчета, трубопроводов, воздуховодов, конструирование гидравлических и воздуходувных машин (компрессоры, насосы, вентиляторы и др.), проектирование котельных агрегатов, а также решения множества других вопросов [1-7].
2. Основные физические свойства жидкости
2.1. Плотность жидкости. Вязкость жидкостей. Капиллярные явления. Аномальные жидкости. Идеальная жидкость
Жидкости с точки зрения механических свойств разделяются на два класса – малосжимаемые (капельные) и сжимаемые (газообразные). С позиций физики капельные жидкости значительно отличаются от газообразных. А в механике жидкости часто законы, которые справедливы для капельных жидкостей, справедливы и для газообразных, и наоборот.
Для большинства случаев рассматриваемых в данном пособии не будет иметь принципиального значения, о какой жидкости будет идти речь – капельной или газообразной. Если же возникнет необходимость – это будет оговариваться отдельно.
Капельные жидкости обладают вполне определенным объемом, величина которого практически не изменяется под действием внешних сил. Газы занимают весь предоставляемый им объем и могут значительно изменять свой объем в зависимости от прилагаемых внешних сил.
Основные свойства жидкости, которые существенно влияют на многие законы их движения – это плотность и вязкость. В некоторых ситуациях также большое значение может иметь сила поверхностного натяжения.
Плотность жидкостей – плотностью жидкости r называется ее масса, заключенная в единице объема:
 (1)
(1)
где М – масса жидкости в объеме W.
Плотность воды при 4° С ρ =1000кг/м3 (102 кгс·с2/м4).
Если жидкость неоднородна, то формула (1) определяет лишь среднюю плотность жидкости. Для определения плотности в данной точке следует пользоваться формулой:
 (2)
(2)
В практических приложениях о массе жидкости судят по ее весу. Вес жидкости, приходящийся на единицу объема, называется удельным весом:
g=G/W, (3)
где G — вес жидкости в объеме W.
Удельный вес воды при 4° С g = 9810 Н/м3 (1000 кгс/м3).
Если жидкость неоднородна, то формула (3) определяет лишь средний удельный вес жидкости. Для определения удельного веса жидкости в данной точке следует пользоваться формулой
 (4)
(4)
где DG — вес жидкости в объеме DW.
Плотность и удельный вес связаны между собой известным соотношением
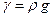 (5)
(5)
где g — ускорение свободного падения.
Относительным удельным весом жидкости (или относительным весом) d называется отношение удельного веса данной жидкости к удельному весу воды при 4°С
 (6)
(6)
В отличие от удельного относительный удельный вес представляет собой отвлеченную (безразмерную) величину, численное значение которой не зависит от выбранной системы единиц измерения. Так, для пресной воды при 4°С имеем
 (7)
(7)
В таблице 1 в качестве примера приведены значения удельного веса и плотности некоторых капельных, а в таблице 2 – сжимаемых жидкостей (газов).
Плотность, а, следовательно, удельный и относительный удельный вес жидкостей меняются с изменением давления и температуры. Эта зависимость различна для капельных жидкостей и газов.
Сжимаемость капельных жидкостей под действием давления характеризуется коэффициентом объемного сжатия βw, который представляет собой относительное изменение объема жидкости на единицу изменения давления
 (8)
(8)
где W0 — первоначальный объем жидкости;
∆ W — изменение этого объема при увеличении давления на величину ∆р.
Коэффициент объемного сжатия в системе СИ имеет размерность Па-1.
Знак минус в формуле (8) обусловлен тем, что положительному приращению давления p соответствует отрицательное приращение (т. е. уменьшение) объема жидкости.
Таблица 1 – Плотность ρ и удельный вес γкапельных жидкостей при 20°С
| Жидкость | γ, Н/м3 | ρ, кг/м3 |
| Анилин | ||
| Бензол | 8590—8630 | 876—880 |
| Бензин авиационный | 7250—7370 | 739—751 |
| Вода пресная | 998,2 | |
| » морская | 10010—10090 | 1002—1029 |
| Глицерин безводный | ||
| Керосин | 7770—8450 | 792—840 |
| Масло касторовое | ||
| » минеральное | 8000—8750 | 877—892 |
| Нефть | 8340—9320 | 850—950 |
| Ртуть | ||
| Спирт этиловый безводный | 789,3 | |
| Хлористый натрий (раствор) | ||
| Эфир этиловый | 7010—7050 | 715—719 |
Таблица 2 – Приближенные значения плотности ρ и удельного веса γгазов при давлении 740 мм рт. ст. и t = 15°С
| Газ | γ, Н/м3 | ρ, кг/м3 |
| Водород | 0,81 | 0,08 |
| Водяной пар | 7,25 | 0,74 |
| Окись углерода | 11,3 | 1,15 |
| Азот | 11,3 | 1,15 |
| Воздух | 11,6 | 1,2 |
| Кислород | 12,8 | 1,3 |
| Углекислота | 17,6 | 1,8 |
Величина, обратная коэффициенту объемного сжатия, называется модулем упругости жидкости
 (9)
(9)
Коэффициент объемного сжатия капельных жидкостей мало меняется при изменении температуры и давления (таблица 4).
Таблица 3 – Значения коэффициента объемного сжатия воды при разных температурах и давлениях
| t 0С |  при давлениях в Па при давлениях в Па
| ||||
| 0,054 | 0,0537 | 0,0531 | 0,0523 | 0,0515 | |
| 0,0529 | 0,0523 | 0,0518 | 0,0508 | 0,0493 | |
| 0,0523 | 0,0518 | 0,0508 | 0,0498 | 0,0481 | |
| 0,0518 | 0,051 | 0,0503 | 0,0488 | 0,047 | |
| 0,0515 | 0,0505 | 0,0495 | 0,0481 | 0,046 |
Таким образом, при повышении давления на 9,8·104 Па (1 ат) объем воды уменьшается на 1/20000 часть первоначальной величины. Коэффициент объемного сжатия для других капельных жидкостей имеет примерно тот же порядок. В подавляющем большинстве случаев, встречающихся в практической деятельности инженера-сантехника, изменения давления не достигают больших величин, и поэтому сжимаемостью воды можно пренебрегать, считая удельный вес и ее плотность не зависящими от давления.
Прочность жидкости на разрыв при решении практических задач не учитывается.
Температурное расширение капельных жидкостей характеризуется коэффициентом температурного расширения bt, выражающим относительное увеличение объема жидкости при увеличении температуры на 10С, т. е.
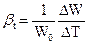 (10)
(10)
где W0 — первоначальный объем жидкости;
∆W — изменение этого объема при повышении температуры на величину ∆T.
Коэффициент температурного расширения капельных жидкостей, как это видно из таблицы 4, незначителен. Так, для воды при температуре от 10 до 20°С и давлении 105Па – bt = 0,00015 1/град.
Таблица 4 - Коэффициент температурного расширения воды
| Давление, Па | bt, 1/град при температуре, °С | ||||
| 1-10 | 10-20 | 40-50 | 60-70 | 90-100 | |
| 0,000014 | 0,00015 | 0,000422 | 0,000556 | 0,000719 | |
| 0,000043 | 0,000165 | 0,000422 | 0,000548 | 0,000714 | |
| 0,000072 | 0,000183 | 0,000426 | 0,000539 | — | |
| 0,000149 | 0,000236 | 0,000429 | 0,000523 | 0,000661 | |
| 0,000229 | 0,000294 | 0,000437 | 0,000514 | 0,000621 |
Однако влияние температуры на удельный вес в ряде случаев (при значительных разностях температур) приходится учитывать.
Плотность и удельный вес капельных жидкостей, как это следует из предыдущих рассуждений, мало изменяются с изменением давления и температуры. Можно приближенно считать, что плотность не зависит от давления, а определяется только температурой. Из выражений (1) и (10) можно найти приближенное соотношение для расчета изменения плотности капельных жидкостей с изменением температуры:
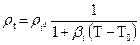 (11)
(11)
Значения коэффициента β t в (11) находятся из таблиц в пределах заданного интервала температур (таблица 4).
Способность жидкостей менять плотность (удельный вес) при изменении температуры широко используется для создания естественной циркуляции в котлах, отопительных системах, для удаления продуктов сгорания и т. д.
В таблице 5 приведены значения плотности воды при разных температурах.
В отличие от капельных жидкостей газы характеризуются значительной сжимаемостью и высокими значениями коэффициента температурного расширения. Зависимость плотности газов от давления и температуры устанавливается уравнением состояния.
Наиболее простыми свойствами обладает газ, разреженный настолько, что взаимодействие между его молекулами может не учитываться – так называемый идеальный газ.
Таблица 5 – Зависимость плотности ρ, кинематической υ и динамической μ вязкости воды от температуры
| Температура, °С | ρ, кг/м3 | υ, м2/с | μ, Па·с |
| 999,9 | 0,00000179 | 0,00179 | |
| 0,00000152 | 0,00157 | ||
| 0,00000101 | 0,00101 | ||
| 0,00000066 | 0,00065 | ||
| 0,00000048 | 0,00048 | ||
| 0,00000037 | 0,00036 | ||
| 0,00000033 | 0,00031 | ||
| 0,00000028 | 0,00027 |
Для идеальных газов справедливо уравнение Клапейрона, позволяющее определять плотность газа при известных давлении и температуре, т.е.
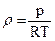 (12)
(12)
где р - абсолютное давление; R - удельная газовая постоянная, различная для разных газов, но не зависящая от температуры и давления (для воздуха R= 287 Дж/(кг·К)); T - абсолютная температура.
Поведение реальных газов в условиях, далеких от сжижения, лишь незначительно отличается от поведения идеальных газов, и для них в широких пределах можно пользоваться уравнениями состояния идеальных газов.
В технических расчетах плотность газа обычно приводят к нормальным физическим условиям (t=0°; р= 101 325 Па) или к стандартным условиям (t=20°С; р=101325 Па), иногда к нормальным техническим условиям (t=15°; р= 98000 Па).
Плотность воздуха при R =287Дж/(кг·К) в стандартных условиях по формуле (12) будет равна r=1,2 кг/м3.
Плотность воздуха при других условиях определяется по формуле
 (13)
(13)
Так как объем газа в большой мере зависит от температуры и давления, выводы, полученные при изучении капельных жидкостей, можно распространять на газы лишь в том случае, если в пределах рассматриваемого явления изменения давления и температуры незначительны. Значительные разности давлений, вызывающие существенное изменение плотности газов, могут возникнуть при их движении с большими скоростями. Соотношение между скоростью движения жидкости и скоростью звука в ней позволяет судить о необходимости учета сжимаемости в каждом конкретном случае. Практически газ можно принимать несжимаемым при скоростях движения, не превышающих 100 м/с.
Вязкость жидкостей. Вязкостью называется свойство жидкостей оказывать сопротивление сдвигу. Все реальные жидкости обладают определенной вязкостью, которая проявляется в виде внутреннего трения при относительном перемещении смежных частиц жидкости. Наряду с легко подвижными жидкостями (например, водой, воздухом) существуют очень вязкие жидкости, сопротивление которых сдвигу весьма значительно (глицерин, тяжелые масла и др.). Таким образом, вязкость характеризует степень текучести жидкости или подвижности ее частиц.
Пусть жидкость течет вдоль плоской стенки параллельными ей слоями (рис. 1), как это наблюдается при ламинарном движении. Вследствие тормозящего влияния стенки слои жидкости будут двигаться с разными скоростями, значения которых возрастают по мере отдаления от стенки.
Рассмотрим два слоя жидкости, двигающиеся на расстоянии ∆y друг от друга. Слой А движется со скоростью и, а слой В — со скоростью u+∆u. Вследствие разности скоростей слой В сдвигается относительно слоя А на

Рис. 1 - Распределение скоростей при течении жидкости вдоль твердой стенки
величину ∆u (за единицу времени). Величина ∆u является абсолютным сдвигом слоя В по слою А, а ∆u/∆у есть градиент скорости (относительный сдвиг). Появляющееся при этом движении касательное напряжение (силу трения на единицу площади) обозначим через τ. Тогда аналогично явлению сдвига в твердых телах мы получим следующую зависимость между напряжением и деформацией:
 (14)
(14)
или, если слои будут находиться бесконечно близко друг к другу,
 (15)
(15)
Величина μ, аналогичная коэффициенту сдвига в твердых телах и характеризующая сопротивляемость жидкости сдвигу, называется динамической или абсолютной вязкостью. На существование соотношения (15) первое указание имеется у Ньютона, и потому оно называется законом трения Ньютона.
Сила внутреннего трения в жидкости
 (16)
(16)
т. е. прямо пропорциональна градиенту скорости, площади трущихся слоев ω и динамической вязкости (тем самым трение в жидкости отличается от трения в твердых телах, где сила трения зависит от нормального давления и не зависит от площади трущихся поверхностей) [1,4].
В международной системе единиц динамическая вязкость выражается в Н∙с/м2 или Па∙с.
В технической системе единиц динамическая вязкость имеет размерность кгс∙с∙м-2. В системе CGS за единицу динамической вязкости принимается пуаз (П) в память французского врача Пуазейля, исследовавшего законы движения крови в сосудах человеческого тела, равный 1 г∙см-1 ∙с-1: 1 Па·с=0,102 кгс·с/м2.
Вязкость жидкостей в сильной степени зависит от температуры; при этом вязкость капельных жидкостей при увеличении температуры уменьшается, а вязкость газов возрастает.
Таблица 6 - Кинематическая и динамическая вязкость капельных жидкостей (при t=20°С)
| Жидкость | μ, Па∙с | υ, м2/с |
| Вода пресная | 0,00101 | 0,000001012 |
| Глицерин безводный | 0,512 | 0,00041 |
| Керосин (при 15° С) | 0,0016-0,0025 | 0,000002-0,000003 |
| Бензин (при 15° С) | 0,0006-0,00065 | 0,00000083-0,00000093 |
| Масло касторовое | 0,972 | 0,01002 |
| » минеральное | 0,0275-1,29 | 0,0000313-0,0145 |
Нефть при 15° С(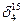 =0,86) =0,86)
| 0,007-0,008 | 0,0000081-0,0000093 |
| Ртуть | 0,0015 | 0,001000011 |
| Спирт этиловый безводный | 0,00119 | 0,00000151 |
Наряду с понятием абсолютной или динамической вязкости в гидравлике находит применение понятие кинематической вязкости, представляющей собой отношение абсолютной вязкости к плотности жидкости:
 (17)
(17)
В международной системе единиц кинематическая вязкость измеряется в м2/с; единицей для измерения кинематической вязкости в системе CGS служит стокс (в честь английского физика Стокса): 1 Ст=1 см2/с=10-4 м2/с.
Кинематическая вязкость газов зависит как от температуры, так и от давления, возрастая с увеличением температуры и уменьшаясь с увеличением давления (таблица 7).
Таблица 7 – Значения кинематической вязкости n и удельной газовой
постоянной R для некоторых газов
| Газ | n, м2/с при температуре в °С | R, Дж/(кг·К) | |||
| Воздух Метан Этилен | 0,0000133 0,0000145 0,0000075 | 0,0000151 0,0000165 0,0000086 | 0,0000178 0,0000197 0,0000104 | 0,0000232 0,0000256 0,00000138 |
Экспериментально вязкость жидкостей определяют вискозиметрами.
Капиллярные явления. Молекулы жидкости, расположенные у поверхности контакта с другой жидкостью, газом или твердым телом, находятся в условиях, отличных от условий внутри некоторого объема жидкости. Внутри объема жидкости молекулы окружены со всех сторон такими же молекулами, вблизи поверхности — лишь с одной стороны. Поэтому энергия поверхностных молекул отличается от энергии молекул в объеме на некоторую величину, называемую поверхностной энергией. Эта энергия пропорциональна площади поверхности раздела s:
Эn = ss (18)
Коэффициент пропорциональности s, называемый коэффициентом поверхностного натяжения, зависит от природы соприкасающихся сред. Этот коэффициент можно представить в виде
σ=-F/l (19)
где F – сила поверхностного натяжения;
l – длина линии, ограничивающей поверхность раздела.
Исходя из определения, s имеет размерность энергии на единицу площади или силы на единицу длины. Для границы раздела вода – воздух при t=20°С коэффициент поверхностного натяжения σ=0,073 Дж/м2, для границы раздела ртуть – воздух коэффициент σ=0,48 Дж/м2.
Поверхностное натяжение жидкости чувствительно к ее чистоте и температуре. Вещества, способные в значительной степени снизить силы поверхностного натяжения, называются поверхностно-активными веществами (ПАВ). При повышении температуры величина поверхностного натяжения уменьшается, а в критической точке перехода жидкости в пар обращается в нуль.
На поверхности раздела трех фаз, например, твердой стенки 1, жидкости 2 и газа 3 между поверхностью жидкости и твердой стенкой образуется так называемый краевой угол θ (рис. 2). Величина краевого угла зависит от природы соприкасающихся сред (от поверхностных натяжений на их границах) и не зависит ни от формы сосуда, ни от действия силы тяжести. Если край жидкости приподнят, ее поверхность имеет вогнутую форму (рис. 2 а) – краевой угол острый. В этом случае жидкость смачивает твердую поверхность. Чем хуже смачивающая способность жидкости, тем больше краевой угол. При θ>90° жидкость считается несмачивающей, при полном несмачивании θ=180°. Капли такой жидкости как бы поджимаются, стараясь уменьшить площадь контакта с твердой поверхностью.
От явления смачивания зависит поведение жидкости в тонких (капиллярных) трубках, погруженных в эту жидкость. В случае смачивания жидкость в трубке поднимается над уровнем свободной поверхности, в случае несмачивания — опускается. Высота капиллярного поднятия (опускания) жидкости находится по формуле
 (20)
(20)
где γ— удельный вес жидкости;
r — радиус трубки.
Во всех явлениях, происходящих при совместном действии сил поверхностного натяжения и сил тяжести, значительную роль играет капиллярная постоянная 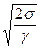 , входящая в выражение (20) и имеющая линейную размерность; для воды при 20° С капиллярная постоянная равна 0,0039 м.
, входящая в выражение (20) и имеющая линейную размерность; для воды при 20° С капиллярная постоянная равна 0,0039 м.

Рис. 2 – Определение краевого угла
Аномальные жидкости. К жидкостям, не подчиняющимся закону вязкости Ньютона (15), так называемым "неньютоновским" (или аномальным) жидкостям, можно отнести, например, литой бетон, глинистый раствор, употребляемый при бурении скважин, нефтепродукты при температуре, близкой к температуре застывания, коллоиды и др.
Опытами установлено, что движение неньютоновских жидкостей начинается только после того, как касательные напряжения достигнут некоторого предельного минимального значения (так называемое начальное напряжение сдвига); при меньших напряжениях эти жидкости не текут, а испытывают только упругие деформации.
В аномальных жидкостях касательное напряжение определяется по формуле Бингема
 (21)
(21)
где τ0 — начальное напряжение сдвига.
Таким образом, в аномальных жидкостях сила трения возникает еще в покоящихся жидкостях, но при стремлении этих жидкостей прийти в движение. На рис. 3 показана зависимость между касательным напряжением и градиентом скорости для нормальных 1 и аномальных 2 жидкостей.

Рис. 3 – Зависимость касательного напряжения от градиента скорости
Вязкость аномальных жидкостей (так называемая структурная вязкость) в отличие от вязкости ньютоновских жидкостей при заданной температуре и давлении непостоянна и изменяется в функции от градиента скорости 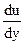 .
.
Поведение различных аномальных жидкостей под нагрузкой и их динамические свойства излагаются в реологии, выводы которой имеют одинаковое значение, как для механики жидкости, так и для теории пластичности.
Идеальная жидкость. В механике жидкости для облегчения решения некоторых задач используется понятие об идеальной жидкости.
Под идеальной жидкостью понимают воображаемую жидкость, лишенную вязкости, абсолютно несжимаемую, не расширяющуюся с изменением температуры, абсолютно неспособную сопротивляться разрыву. Таким образом, идеальная жидкость представляет собой некоторую модель реальной жидкости. Выводы, полученные исходя из свойств идеальной жидкости, приходится, как правило, корректировать, вводя поправочные коэффициенты.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 368; Нарушение авторских прав?; Мы поможем в написании вашей работы!