Шушляков Д. А. 5 страница

Сопоставляя формулу (117) с общей зависимостью для потерь напора на трение, имеющей вид

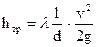
найдем

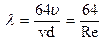. (118)

Отсюда следует, что при ламинарном режиме коэффициент гидравлического трения обратно пропорционален числу Рейнольдса.

Полученные зависимости с большой точностью подтверждаются многочисленными опытами над движением различных жидкостей в условиях ламинарного режима. Тем самым находят подтверждение и сделанные в процессе выводов этих зависимостей допущения о применимости закона Ньютона для ламинарного движения и отом, что скорость у стенки равна нулю. В инженерной практике с ламинарным режимом часто приходится сталкиваться при движении в трубах жидкостей с повышенной вязкостью (нефть, керосин, смазочные масла и пр.).

Из формулы (117) видно, что потери напора при ламинарном режиме прямо пропорциональны вязкости жидкости. Поэтому иногда для повышения пропускной способности нефтепроводов нефть в холодную погоду подогревают, благодаря чему уменьшается ее вязкость, а, следовательно, и потери напора. Полученные зависимости требуют внесения в них поправок при движениях со значительным теплообменом, т. е. в случаях, если движение жидкости сопровождается ее нагреванием или охлаждением;

Часто вместо гидравлического радиуса используют так называемый эквивалентный (или гидравлический) диаметр

.

Напомним, что для круглых труб эквивалентный диаметр равен их геометрическому диаметру: d_экв=d.

Заменяя в формуле Дарси для потери напора диаметр гидравлическим радиусом или эквивалентным диаметром, получаем выражение

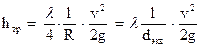, (119)

которое принципиально пригодно для расчета труб любого поперечного сечения.

Однако в формуле (119) коэффициент l зависит уже не только от числа Рейнольдса, но и от формы сечения трубы.

При ламинарном движении коэффициент λ в трубах некругового сечения значительно возрастает по сравнению с движением в круглой трубе (при одном и том же числе Рейнольдса) и может быть выражен формулой

, (120)

где Re_ - число Рейнольдса, вычисленное по эквивалентному диаметру;

;

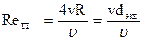А – коэффициент формы, численные значения которого зависят от формы сечения.

5.7. Опытные данные о распределении скоростей и потерях напора

Два основных вопроса, которые интересуют инженера при рассмотрении турбулентного движения жидкости в трубах, — это определение потерь напора и распределения скоростей по поперечному сечению трубы. Опыты показывают, что как распределение скоростей, так и потери напора могут сильно меняться в зависимости от диаметра трубы, скорости движения, вязкости жидкости и шероховатости стенок труб. При этом шероховатость стенок в свою очередь определяется рядом факторов: материалом стенок; характером механической обработки внутренней поверхности трубы, от чего зависят высота выступов шероховатости, их форма, густота и характер их размещения на поверхности; наличием или отсутствием в трубе ржавчины, коррозии, отложения осадков, защитных покрытий и т. д.

Рис. 32 – К понятию об абсолютной шероховатости

Для грубой количественной оценки шероховатости вводится понятие о средней высоте выступов (бугорков) шероховатости. Эту высоту, измеряемую в линейных единицах (рис. 32), называют абсолютной шероховатостью и обозначают буквой k. Опыты показали, что при одной и той же величине абсолютной шероховатости влияние ее на величину гидравлических сопротивлений и распределение скоростей различно в зависимости от диаметра трубы. Поэтому вводится понятие об относительной шероховатости, измеряемой отношением абсолютной шероховатости к диаметру трубы, т. е. величиной k/d.

С помощью анализа размерностей было установлено что коэффициент гидравлического трения λ в формуле Дарси-Вейсбаха 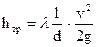может зависеть от двух безразмерные параметров: vdρ/μ и k/d.Первый из этих параметров представляет собой число Рейнольдса, а второй относительную шероховатость, а, следовательно,

. (121)

0,4 0,2

2,6 3.0

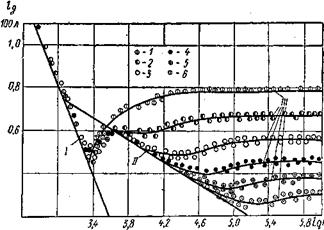
Рис. 33 – График Никурадзе (I – линия ламинарного движения; II – линия гидравлически гладких труб; III – линия вполне шероховатых труб;

1 – r/k=15; 2 – r/k=30,6; 3 – r/k=60; 4 – r/k=126; 5 – r/k=252; 6 – r/k=507

Первые систематические опыты для выявления характера зависимости λ от Re и k/dбыли проведены в 1933 г. И. Никурадзе в гладких латунных трубах и трубах с искусственной равномерно-зернистой шероховатостью из кварцевого песка. Песок с различной высотой бугорков шероховатости kнаносился сплошным слоем на внутреннюю поверхность труб разного диаметра; при этом были получены различные значения относительно шероховатости (от k /d=0,00197 до k /d=0,066). В изготовленных таким образом трубах при разных расходах измеряли потерю напора и вычисляли коэффициент λ, по формуле Дарси-Вейсбаха.

Результаты опытов Никурадзе представлены в виде графика; показанного на рис. 33, где по горизонтальной оси отложены величины 1g Re, а по вертикальной – величины 1g(100λ). Израссмотрения этого графика можно сделать следующие выводы.

При ламинарном движении (Re<2300 или lgRe<3,6) все опытные точки, независимо от шероховатости стенок, ложатся на прямую линию I; эта линия изображает зависимость (121) для ламинарного режима. Таким образом подтверждается, что при ламинарном движении шероховатость не оказывает влияния на сопротивление.

При турбулентном режиме (Re>2300; lgRe>3,6) опытные точки до некоторых чисел Рейнольдса совпадают с линией II, полученной при испытании гладких труб без искусственной шероховатости, а затем отклоняются от нее в сторону больших значений λ; чем меньше шероховатость, тем при больших числах Рейнольдса начинается это отклонение; таким образом, при некоторых условиях (малые числа Re, малые значения k/dили большие r/k,где r — радиус трубы) шероховатость не оказывает влияния на сопротивление также и при турбулентном движении.

При больших числах Рейнольдса коэффициент гидравлического трения перестает зависеть от этого числа (т. е. от вязкости жидкости) и для заданного значения k/dсохраняет постоянную величину.

Трубы, в которых коэффициент гидравлического трения λ вовсе не зависит от вязкости жидкости (числа Рейнольдса), а только от относительной шероховатости, называют вполне шероховатыми. Трубы же, в которых коэффициент λ, вовсе не зависит от шероховатости стенок, а только от числа Рейнольдса, называют гидравлически гладкими. Из графика Никурадзе видно, что одна и та же труба в одних условиях может быть гидравлически гладкой, а в других вполне шероховатой. Область движения, в которой λ зависит и от Re, и от k/d, называют переходной (область смешанного трения).

Полученным результатам можно дать следующее физическое истолкование. При малых числах Рейнольдса жидкость обтекает выступы шероховатости без образования и отрыва вихрей благодаря значительному влиянию вязкости жидкости; свойства поверхности стенок труб не оказывают при этом влияния на сопротивление и кривые λ = f(Re) совпадают с прямой II (для гладких труб). Когда же с увеличением скорости (т. е. числа Рейнольдса) от бугорков шероховатости начинают отрываться вихри, то свойства поверхности уже оказывают влияние на сопротивление и кривые λ = f(Re) отклоняются от линии гладкого трения.

В результате опытов Никурадзе и других исследований над сопротивлением трубопроводов были предложены различные эмпирические формулы для определения коэффициента гидравлического трения λ.

Для гидравлически гладких труб широкое распространение получила формула Блазиуса

. (122)

а для вполне шероховатых труб — формула Б. Л. Шифринсона:

. (123)

5.8. Местные гидравлические сопротивления. Общие сведения

Местные сопротивления вызываются фасонными частями, арматурой и другим оборудованием трубопроводных сетей, которые приводят к изменению величины или направления скорости движения жидкости на отдельных участках трубопровода (при расширении или сужении потока, в результате его поворота, при протекании потока через диафрагмы, задвижки и т. д.), что всегда связано с появлением дополнительных потерь напора.

В водопроводных магистральных трубах потери напора на местные сопротивления обычно весьма невелики (не более 10-20% потерь напора на трение). В воздухопроводах вентиляционных и пневмотранспортных установок, в дутьевых установках котельных потери на преодоление местных сопротивлений часто значительно больше потерь напора на трение. Местные сопротивления являются весьма существенными и при расчете паропроводов.

Потери напора, затраченного на преодоление какого-либо местного сопротивления, принято оценивать в долях скоростного напора, соответствующего скорости непосредственно за рассматриваемым местным сопротивлением, т. е. определять их из формулы Вейсбаха

,

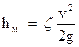где ζ — так называемый коэффициент местного сопротивления.

Коэффициенты разных местных сопротивлений находят, как правило, опытным путем; таблицы значений этих коэффициентов (или эмпирические кривые и формулы для них) содержатся во всех инженерных справочниках и руководствах по гидравлике [3, 6, 7]. Для некоторых практически важных случаев значения коэффициентов местных сопротивлений удалось получить также теоретическим путем.

Иногда местные потери напора выражают в виде эквивалентной длины l _э прямого участка трубопровода, сопротивление трения которого по величине равно рассматриваемым местным потерям напора, т. е. из условия

,

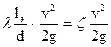или

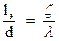. (124)

Коэффициент гидравлического трения λ как уже было выяснено, зависит от числа Рейнольдса и относительной шероховатости, поэтому одному и тому же значению коэффициента местного сопротивления ζ в общем случае соответствует разная эквивалентная длина. Лишь в квадратичной области сопротивления, когда λ ≠ f (Re), эквивалентная длина заданного местного сопротивления постоянна.

Основные виды местных потерь напора можно условно разделить на следующие группы:

- потери, связанные с изменением сечения потока (или, что то же, его средней скорости). Сюда относятся случаи внезапного расширения, сужения, а также постепенного расширения и сужения потока;

- потери, вызванные изменением направления потока. Сюда относятся различного рода колена, угольники, отводы, используемые на трубопроводах;

- потери, связанные с протеканием жидкости через арматуру различного типа (вентили, краны, обратные клапаны, сетки, отборы, дроссель-клапаны и т. д.);

- потери, связанные с отделением одной части потока от другой или слиянием двух потоков в один общий. Сюда относятся, например, тройники, крестовины и отверстия в боковых стенках трубопроводов при наличии транзитного расхода.

6. Задачи

Задача 1.

Определить коэффициент объемного сжатия β_w, если известно, что начальный объем капельной жидкости W₀=5 м³, возрастание давления в процессе составляет Δр=12 кПа, а изменение объема составляет ΔW=0,05 м³.

Решение:

Используем формулу (8), тогда:

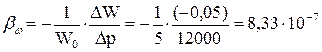Па^-1.

Задача 2.

Определить число Рейнольдса для холодной воды (t=20°С), которая движется в трубопроводе диаметром 200 мм, если расход воды составляет 12 м³/час.

Решение:

Приводим все величины в систему СИ, для этого необходимо м³/час перевести в м³/с: 12/3600=0,0033 м³/с; переводим мм в м – 200 мм=0,2 м.

Рассчитываем площадь трубы F=(p×0,2²/4)=0,0314 м².

Рассчитываем скорость воды в трубопроводе v=0,0033/0,0314=0,105 м/с. Из таблицы 5 определяем, что при t=20°С n=1,006∙10^-6 м²/с.

Используя формулу 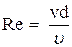=0,105∙0,2/1,006∙10^-6=19811>10000 – режим турбулентный.

Задача 3.

Определить потери давления в трубопроводе диаметром d=0,9 м, при расходе холодной воды (t=20°С) G=0,001 м³/с. Трубы стальные новые (рис. 34).

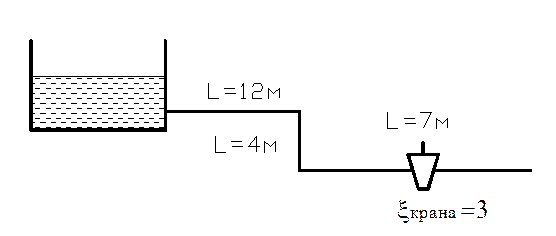
Рис. 34 – Расчетная схема

Решение:

Рассчитываем скорость потока жидкости v=G/F, м/с. v=0,001/(p×0,9²/4)=0,0016 м/с.

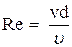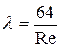
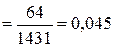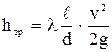
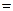
Используя формулу =0,0016∙0,9/1,006∙10^-6=1431‹2300 – режим ламинарный. Тогда для определения коэффициента гидравлического трения используем формулу (118): ; потери давления на трение 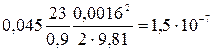кгс/м².

Для определения потерь давления на местных сопротивлениях определяем, какие сопротивления есть на схеме – кран пробковый (ζ=3), колено под 90° – 2 шт. (ζ=1,1·2=2,2), вход в трубопровод (ζ=0,5).

кгс/м².

Общие потери давления DР=(1,5+7,4)∙10^-7=8,9∙10^-7 кгс/м².

Список литературы

1. Альтшуль А.Д., Киселев П.Г. Гидравлика и аэродинамика (Основы механики жидкости). Учебное пособие для вузов. Изд. 2-е, перераб. и доп. М. Стройиздат, 1975, 323 с.

2. Тихомиров К.В., Сергеенко Э.С. Теплотехника, теплогазоснабжение и вентиляция: Учеб. для вузов. – 4-е изд., перераб. и доп. – М.: Стройиздат, 1991. – 480 с.

3. Альтшуль А.Д., Калицун В.И. Гидравлические сопротивления трубопроводов. – М.: Изд-во лит-ры по стр-ву. 1964. 285 с.

4. Лойцянский Л.Г. Механика жидкости и газа. – М.: "Наука". 1973. – 848 с.

5. Шлихтинг Г. Теория пограничного слоя. – М.: "Наука". 1974. – 712 с.

6. Шушляков А.В., Паламарчук О.Ю., Шушляков Д.А. Вентиляция гражданского здания. – Х.: ФОП Костинский А.В., 2011. – 326 с.

7. Інженерне обладнання будівель: навч. посібник /
М.О. Шульга, Д.О. Шушляков, Г.А. Усик; Харк. нац. акад. міськ. госп-ва. – Х: ХНАМГ, 2011. – 352 с.

Учебное издание

ШУШЛЯКОВ Дмитрий Александрович

ТЕХНИЧЕСКАЯ МЕХАНИКА ЖИДКОСТЕЙ И ГАЗОВ

КОНСПЕКТ ЛЕКЦИЙ

Ответственный за выпуск к.т.н., доц. В.И. Абелешев

Под авторской редакцией

Компьютерная верстка _____________________

План 2013 г., поз. 173 л

Подп. к печати 28.10.2013	Формат 60×84 1/16
Печать на ризографе	Усл. печ. лист.
Зак. №	Тираж 200 экз.

Видавець і виготовлювач:

Харківський національний університет міського господарства

ім. О.М. Бекетова

вул. Революції, 12, Харків, 61002

Електронна адреса: [e-mail]

Свідоцтво суб’єкта видавничої справи

ДК №4064 від 12.05.2011р.

Дата добавления: 2014-12-26