Шушляков Д. А. 2 страница

3. Равновесие капельных жидкостей

3.1. Равновесное состояние жидкости и действующие силы

Равновесное состояние. Если на некоторую массу жидкости не действовали и не действуют внешние силы, то каждая частица этой массы или остается неподвижной относительно данной системы координат, или движется прямолинейно с одинаковой для всех частиц скоростью, так что взаимное расположение частиц этой массы жидкости остается неизменным. Такое механическое состояние массы жидкости называется равновесным.

При действии внешних сил рассматриваемая масса жидкости может или сохранить равновесное положение, или перейти в состояние движения. Для равновесия необходимо, чтобы эти силы удовлетворяли некоторым условиям, которые будут рассмотрены далее.

Внешние силы могут быть поверхностными и объемными (массовыми).

Поверхностные силы – это силы, действующие в точках граничной поверхности данной массы. Они пропорциональны размеру площадки ∆ω, взятой на этой поверхности, для которой можно написать равенство:

∆Р=p∆ω (22)

где ∆Р – действующая поверхностная сила, а р – коэффициент пропорциональности, физический смысл которого очевиден из отношения p=∆Р/∆ω, то есть этот коэффициент представляет собой так называемое "напряжение". Объемные (или массовые) силы – это внешние силы, пропорциональные объему жидкости (если данная масса однородна, т. е. плотность ее одинакова во всем объеме). Для объемных сил справедлива зависимость

∆R= k ∆W (23)

где k – коэффициент пропорциональности, физический смысл которого заключается в условии k =ρj (здесь ρ – плотность, а j – ускорение данной объемной силы).

Условия действия поверхностных сил при равновесии жидкости. Рассмотрим условия, которым должны удовлетворять поверхностные силы при равновесии жидкости.

Представим некоторую массу жидкости, находящуюся в равновесном состоянии (рис. 4). Пусть в некоторой точке М ее граничной поверхности действует сила R. При этом силу R можно рассматривать как равнодействующую всех сил, которые действуют в этой точке [1,4]. Разлагая эту силу по направлению нормали и касательной к граничной поверхности в этой точке, мы найдем две силы: силу N — нормальную к указанной поверхности и силу Т — касательную к той же поверхности.

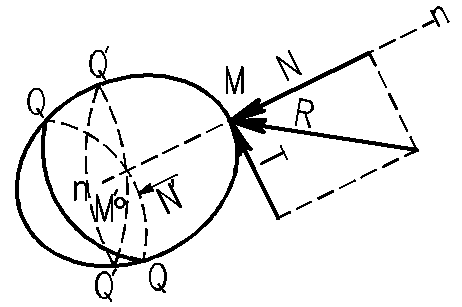
Рис. 4 – Действие поверхностных сил при равновесии жидкости

Сила N сжимает частицу М, и, поскольку жидкость сопротивляется сжатию, в этой точке (где расположена частица) может возникнуть реакция, которая уравновесит силу N – следовательно, частица М останется в равновесии. Сила Т — касательная сила — стремится сдвинуть частицу М., Чтобы сдвига не произошло и равновесное состояние не нарушалось, необходимо соблюдение условия Т=0, или, иначе, для равновесия частицы М необходимо, чтобы равнодействующая сила R, действующая на частицу М, была направлена (по внутренней нормали n) к граничной поверхности, т. е. была сжимающей, а не растягивающей силой.

Отсюда следует вывод — для сохранения равновесия массы жидкости необходимо, чтобы внешние силы, действующие в точках ее граничной поверхности, были направлены только по внутренним нормалям к этой поверхности.

Взаимодействие между частицами покоящейся жидкости. Рассмотрим силовое взаимодействие между частицами внутри массы жидкости. С этой целью пересечем пространство, занятое покоящейся жидкостью, произвольной поверхностью Q (рис. 4), которая разделит массу жидкости на две части — верхнюю и нижнюю. Рассмотрим затем равновесие, например, нижней части.

Поверхность Q в пределах сечения является граничной поверхностью этой части. Поэтому на частицу М', лежащую на этой поверхности, окружающие ее частицы верхней части действуют с некоторой сжимающей силой N'. Ввиду произвольности выбора секущей поверхности Q можем (проводя через точку М' произвольные поверхности Q1, Q2 и т. д.) сделать вывод, что все частицы внутри покоящейся массы жидкости испытывают всестороннее сжатие.

3.2. Гидростатическое давление в точке

Рассмотрим площадку ∆ω, на которую действует сила ∆ Р (рис. 5). Отношение p =∆Р/∆ω, очевидно, представляет собой "напряжение", т. е. силу, приходящуюся на единицу площади.

Так как при равновесии жидкости ∆Р является сжимающей силой, то р представляет собой среднее для данной площадки напряжение сжатия, которое называют средним гидростатическим давлением на площадке. Для получения точного значения р в данной точке надо определить предел этого отношения при

∆ω→0, что и определит гидростатическое давление в данной точке:

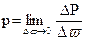(24)

Размерность [ р ]равна размерности напряжения, т. е., [ р ]= [Па] или [кгс/м²].

Рис. 5 – Сила, воздействующая на единицу площади

Основная теорема гидростатики. Величина гидростатического давления в данной точке не зависит от ориентации в пространстве площадки, на которой она расположена, т. е.

p_x=p_y=p_z=p_n (25)

где рx, р_у, p_z — гидростатические давления по направлению координатных осей, а р_п — то же, по произвольному направлению п.

Для доказательства выберем внутри массы жидкости, находящейся в равновесии, объем в форме тетраэдра (рис. 6) и, полагая его отвердевшим, напишем для него (как для твердого тела) условия равновесия в виде трех уравнений проекций действующих сил и трех уравнений моментов:

ΣX=0 и ΣMx=0 (26)

ΣY=0 и ΣMy=0 (27)

ΣZ=0 и ΣMz=0 (28)

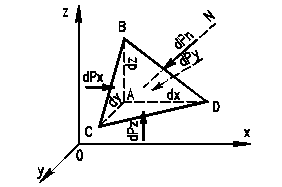
Рис. 6 – К теореме о независимости гидростатического давления от направления

При уменьшении объема тетраэдра в пределе до нуля система действующих сил преобразуется в систему сил, проходящих через одну и ту же точку, и, таким образом, уравнения моментов теряют смысл.

Составим уравнение проекций сил на ось Ох.

На рассматриваемый тетраэдр действуют четыре поверхностные силы (по числу граней тетраэдра), направленные по нормалям к соответствующим граням, и объемная сила dF. Проектируя эти силы на ось Ох, получим

(29)

где , ,

так как d ω cosα представляет собой проекцию площадки d ω на плоскость, перпендикулярную оси Ох.

Объемная сила dF= dmj, где dm — масса тетраэдра, равная р1/6 dxdydz, а j — ускорение, создаваемое этой силой.

Тогда dF cosα = dmj cosα.

Введем обозначение j·cosa =X, j·cosb=У, j·cosg=Z, где X, Y и Z — проекции ускорения внешней объемной силы (эти обозначения будут использоваться и далее).

После соответствующих подстановок получим уравнение

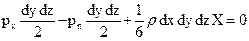(30)

- сокращая которое на — dydz, найдем

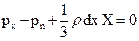(31)

Опуская третье слагаемое как величину высшего порядка малости по сравнению с двумя первыми, получим

р_х-р_п= 0 (32)

Очевидно, по аналогии можем написать

р_y-р_n =0 и р_z-р_n =0 (33)

или, наконец,

р_х = р_y = р_z=р_n (34)

что доказывает теорему.

Гидростатическое давление в точке, будучи одинаковым по любому направлению, неодинаково в различных точках пространства, т. е. р есть функция координат: p=f(x,y,z).

3.3. Общие дифференциальные уравнения равновесия жидкости

Уравнение Эйлера. Выберем внутри покоящейся жидкости параллелепипед с ребрами, расположенными параллельно координатным осям 0 х, 0 у и 0 z (рис. 7) и равными соответственно dx, dy и dz. Составим уравнения равновесия этого параллелепипеда в виде уравнений проекций сил (согласно предыдущим рассуждениям уравнения моментов теряют смысл): ΣX=0, ΣY=0, ΣZ=0.

Проектируя силы на ось 0 х, согласно рис. 7, имеем

ΣX=dP-dP₁+dF·cosα=0 (35)

Определим каждое из слагаемых. Поверхностные силы равны: dP=pdydz и dP₁=p’dydz, где р и р^' — средние гидростатические давления соответственно на площадки ABCDA и A'B'C'D'A'.

Рис. 7 – К выводу уравнений равновесия жидкости

Так как гидростатическое давление является функцией координат, среднее гидростатическое давление на площадке A'B'C'D'A' будет равно:

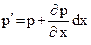(36)

потому что при переходе от площадки ABCDA к площадке A'B'C'D'A' изменяется только координата х. Следовательно, сила

объемная сила для массы dm=pdxdydzравна:

dF cos α = dmj cos α = dmX = rdx dy dzX.

Подставляя в (35) значения слагаемых, запишем

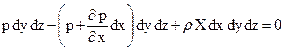(37)

Раскрывая скобки и (после приведения подобных членов) сокращая на dx dy dz, получим уравнение проекций сил на ось 0 х в виде

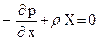(38)

Аналогично можно получить и уравнения проекций сил на оси Оу и Оz, в результате чего система трех уравнений равновесия жидкости (уравнения Эйлера) запишется в виде

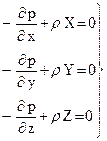(39)

Основное дифференциальное уравнение гидростатики. Перепишем уравнения Эйлера в несколько другом порядке:

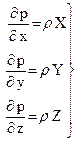(40)

умножив каждое из этих уравнений соответственно на dx, dy и dz и произведя сложение правых и левых частей уравнений, получим

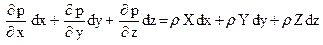(41)

Так как гидростатическое давление р зависит только от трех независимых переменных координат х, у и z, левая часть этого равенства представляет собой полный дифференциал функции p=f(х,у,z):

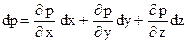(42)

Делая подстановку, находим окончательно

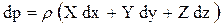(43)

Уравнение (43) называется основным дифференциальным уравнением гидростатики,так как его использование позволяет решать основные задачи гидростатики.

Рассмотрим это уравнение более подробно.

Прежде всего, отметим, что, так как dp есть полный дифференциал, то выражение в скобках правой части будет также полным дифференциалом некоторой функции координат, т. е.

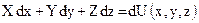(44)

Следовательно,

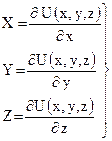(45)

Здесь величины X, Y и Z, т. е. проекции ускорения объемной силы, можно рассматривать как проекции самой объемной силы, отнесенной к единице массы данной жидкости, так как

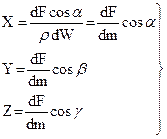(46)

поэтому функция U (x, у, z) является потенциалом сил или так называемой "силовой функцией". Таким образом, равновесие жидкости возможно, если объемные силы имеют потенциал.

Правую часть уравнения (43) можно рассматривать и как уравнение элементарной работы dT, т. е. можем написать

ρX dx+ρY dy+ρZ dz=dT (47)

Действительно, работа силы 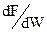(силы, отнесенной к единице объема) на пути ds (рис. 8) равна:

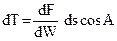(48)

где А — угол между направлением действия силы dF/dW и линией перемещения ds.

Но из (48) следует:

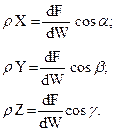(49)

и кроме того dx=ds cos a; dy=ds cos b; dz=ds cos c.

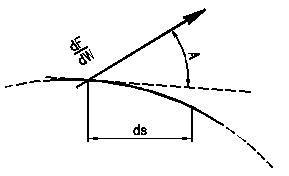
Рис 8 – Работа силы dF/dW на пути ds

С учетом последнего слагаемые левой части уравнения (47) равны по отдельности:

(50)

в сумме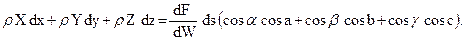

Если учесть, что cos α cos a+cosβ cos b+cos γ cos с = cos A, приходим к равенству:

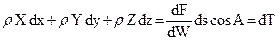(51)

Это и доказывает справедливость уравнения (47).

Отсюда заключаем, что изменение гидростатического давления dp равно работе внешних объемных сил, совершаемой на пути изменения давления от р₁до p₂(при р₂ - p₁ = dp ).

Характеристическое уравнение. В основном дифференциальном уравнении гидростатики (42) неизвестны две величины: р и ρ (значения X, Y и Z, а также координаты точки обычно заданы.) Таким образом, для определенности решения необходимо иметь еще одно независимое уравнение, в качестве которого используется так называемое характеристическое уравнение, определяющее собой особенности данной жидкости.

Например, рассматривая равновесие капельной жидкости и считая ее абсолютно несжимаемой, характеристическим уравнением будет условие

ρ = const, (52)

а для газа – уравнение Бойля-Мариотта pw= RT, или p/r=RT.

В общем виде условия равновесия можно записать в виде функции, характеризующей особенности сжатия данной жидкости:

ρ = φ(Р,t°) (53)

Поверхность уровня. Поверхностью уровня называется такая поверхность, все точки которой имеют одно и то же значение рассматриваемой функции: например, поверхность равной температуры (изотермическая поверхность), поверхность равного потенциала и т. д.

Для рассмотрения задач гидравлики важное значение имеет поверхность равного давления. Имея в виду в дальнейшем изложении именно поверхность равного давления, будем условно называть ее кратко поверхностью уровня.

Уравнение поверхности уровня и свойства этой поверхности. Так как во всех точках поверхности уровня гидростатическое давление одинаково, т. е. р = const, то dp=0 и из основного дифференциального уравнения гидростатики получим

ρ(Xdx+Ydy+Zdz)=0 (54)

Так как плотность ρ≠0, то

Xdx+Ydy+Zdz=0 (55)

где X, Y и Z — функции координат.

Уравнение (55) представляет собой дифференциальное уравнение поверхности, для которой р = const, т. е. уравнение поверхности уровня.

Рассмотрим свойства поверхности уровня:

1. Две поверхности уровня не пересекаются между собой. Действительно, допустим, что поверхность давления р1пересекается с поверхностью давления р2,тогда в точках линии пересечения этих поверхностей давление было бы одновременно равным и р1и р2, что невозможно, так как р1 ≠ р2. Следовательно, пересечение этих поверхностей невозможно.

2. Внешние объемные силы направлены нормально к поверхности уровня. Подтвердить это положение можно так. Работа силы F. на элементарном пути ds согласно (47) равна:

dT = ρ (Xdx + Ydy + Zdz) (56)

Но для поверхности уровня трехчлен в скобках равен нулю поэтому работа силы F на пути ds вдоль поверхности уровня равна нулю (dT=0).

С другой стороны, согласно рис. 8 работа силы F=dT=F cos A ds, и поскольку dT=0, a f ≠0 и ds ≠0, то cos A должен быть равен нулю, т. е. угол A=π/2.

3.4. Равновесие капельной жидкости в поле земного тяготения

Поверхность уровня. Рассмотрим равновесие жидкости в поле земного тяготения в пределах небольшой ограниченной области. Тогда ускорения свободного падения в различных точках этого пространства будут параллельны и направлены вертикально. Расположим координатную ось 0 z вертикально; при этом ускорение свободного падения g=9,81 м/с² будет направлено параллельно оси 0 z.

Составим уравнение поверхности уровня, учитывая, что для данного случая равновесия жидкости величины X, Y и Z, входящие в общее дифференциальное уравнение поверхности уровня (55), будут равны соответственно: X=g_x=0; Y=g_y=0; Z=g_z=-g, при этом g_x, g_y, g_z— проекции ускорения gпо координатном осям. Подставляя эти значения в уравнение (55), получим дифференциальное уравнение поверхности уровня для рассматриваемых условий -gdz=0, или dz = 0. Интегрируя это уравнение, находим

-gz=const или z=const=С (57)

Так как C=const – произвольная постоянная, то это уравнение будет уравнением семейства горизонтальных плоскостей (параллельных осям 0 х и 0 у).

Итак, поверхность уровня есть горизонтальная плоскость.

Распределение гидростатического давления. Воспользуемся основным дифференциальным уравнением гидростатики dp=ρ(Xdx+Ydy+Zdz)

В случае равновесия жидкости в поле земного тяготения Х=0, У=0, a Z=- g. Поэтому основное уравнение получим в виде

dp=-ρgdz (58)

Но произведение pg=γ, где γ — удельный вес данной жидкости.

Делая подстановку и деля обе части уравнения (58) на γ, перепишем его в следующем виде:

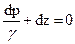(59)

интегрируя, найдем (при g= const)

(60)

Чтобы определить постоянную интегрирования С, рассмотрим резервуар, наполненный водой (рис. 9), со свободной поверхностью (атмосферное давление). Тогда для точки А, лежащей на поверхности, р = р₀ и z=z₀подставив эти значения в (60), находим, что произвольная постоянная интегрирования

(61)

и уравнение (60) запишется в виде

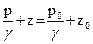(62)

Или

p=p0+γ(z0-z) (63)

Последнее уравнение называют основным уравнением гидростатики.

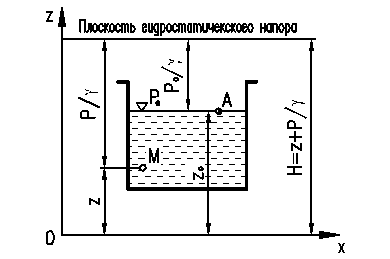
Рис. 9 – К определению постоянной интегрирования

Рассмотрим уравнение (62) более подробно. Все слагаемые, входящие в него, имеют линейную размерность; zи z₀ – координаты свободной поверхности и произвольной точки М, т. е. высоты расположения свободной поверхности и точки М; ро/γ и р/γ – высоты, соответствующие гидростатическому давлению на поверхности р_о и р в точке М.

Очевидно, что постоянная интегрирования С имеет также линейную размерность; обозначим ее через H.

Величины zи p/γ часто называют в гидравлике геометрической и пьезометрической высотами, тогда H как сумма двух высот будет также высотой – ее называют гидростатическим напором. Согласно рис. 9, величина H представляет собой ординату горизонтальной плоскости, именуемой плоскостью гидростатического напора. Эта плоскость расположена выше плоскости свободной поверхности на высоту р_о/γ.

Уравнение (60) можно рассматривать и как уравнение энергии.

Действительно, все слагаемые в этом уравнении имеют линейную размерность.

Умножим это уравнение на размерную величину 1 Н (силу); тогда (не записывая единицы) все слагаемые приобретут размерность работы или энергии [Дж]. Очевидно, что уравнение это будет определять потенциальную энергию, подсчитанную для массы жидкости весом 1Н. Назовем ее удельной энергией. В этом случае уравнение (60) можно прочитать так: сумма удельной потенциальной энергии положения z и удельной потенциальной энергии давления p/g есть величина постоянная во всех точках данной покоящейся массы жидкости.

Измерение давления в данной точке. Гидростатическое давление более удобно вычислять по формуле (63). Так как разность (z₀-z) представляет собой глубину h погружения данной точки под уровень свободной поверхности, то можно написать уравнение (63) в виде

p=p₀+ γh (64)

Именно в такой записи и используют это уравнение для вычисления гидростатического давления.

Итак, давление можно измерить двумя способами: по уравнению (64) в единицах напряжения сжатия р или по уравнению (63) в линейных единицах высоты столба данной жидкости p/y.

Закон Паскаля. Из уравнения (64) видно, что в любой точке жидкости (на любой глубине h) гидростатическое давление зависит от величины внешнего давления р_о на свободной поверхности. При увеличении внешнего давления точно на ту же величину увеличится и давление в данной точке. Таким образом, жидкость обладает свойством передавать внешнее давление всем расположенным внутри ее частицам жидкости без изменения. В этом заключается закон Паскаля.

3.5. Абсолютное и избыточное давление. Вакуум

Абсолютным давлением р называется гидростатическое давление, определяемое по формуле (64).

Из этой формулы следует, что абсолютное давление слагается из двух составляющих: внешнего давления 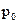, передаваемого жидкостью по закону Паскаля, и давления, определяемого величиной γh. Последнее называют относительным или, если на свободной поверхности жидкости действует атмосферное давление, избыточным давлением. Исходя из принятой формулировки формулу (64) можно переписать в следующем виде:

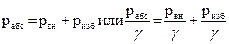(65)

где избыточное давление

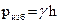
(66)

Из последнего равенства следует, что избыточное давление изменяется с глубиной по линейному закону

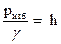(67)

и в координатах р/у и h изобразится в виде биссектрисы координатного угла [1].

Абсолютное давление не может быть отрицательным, так как жидкость не сопротивляется растяжению. Избыточное давление как разность 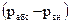может быть и больше, и меньше нуля, т. е. отрицательное избыточное давление называют вакуумметрическим давлением, т.е.

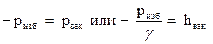
(здесь hвак называется вакуумметрической высотой). Можно написать

;

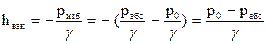тогда вакуумметрическая высота выразится формулой

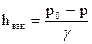. (68)

Вакуумметрическая высота h_вак возрастает по величине с уменьшением абсолютного давления и в пределе, когда р_абс = 0 (отрицательным абсолютное давление быть не может), достигает максимума 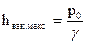, т. е. величины атмосферного давления.

3.6. Давление жидкости на плоские стенки. Центр давления

Определение силы давления. Предположим, что плоская стенка, ограждающая некоторую массу неподвижной жидкости, наклонена к горизонту под углом α. Определим силу Р, с которой жидкость действует на выбранную в пределах этой стенки площадку 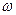(рис. 10).

В каждой точке на этой площади гидростатическое давление равно р и отвечает формуле р = 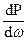, где dP — элементарная сила, а dω - элементарная площадка.

Следовательно, сила, с которой жидкость действует на элементарную площадку dω, будет равна dP = pdω. Эта сила направлена по нормали к плоскости стенки. Аналогично будет определяться сила давления жидкости на любую другую элементарную площадку dω. Поэтому искомую силу Р, с которой покоящаяся жидкость действует на площадь 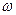, можно найти как равнодействующую системы параллельных сил dP, равную их алгебраической сумме.

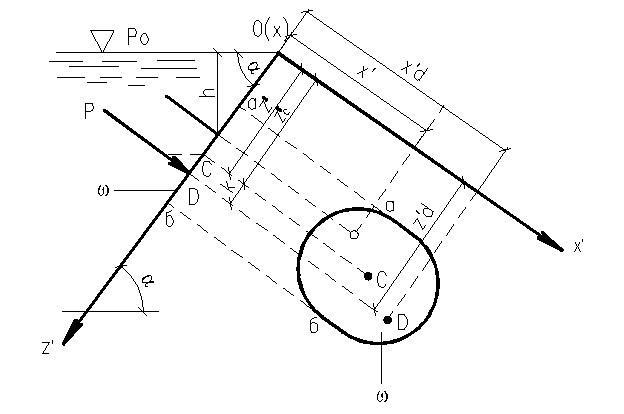
Рис. 10 – К определению силы давления на плоскую стенку

Итак, искомая сила

.

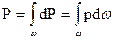Но в любой точке гидростатическое давление 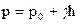, откуда

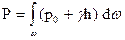(69)

Ориентируем данную площадь относительно соответственно расположенных координат осей. Примем за ось 0xлинию пересечения свободной поверхности воды с плоскостью стенки и направим координатную ось 0z' * вниз вдоль стенки (рис. 10).

В этой координатной системе все точки определяются координатами x́́'и ź', поэтому глубину h выразим через ź', а именно: h=z' sin .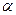

Итак, силу Р можно определить по формуле

,

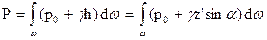или

(70)

Для определения интеграла 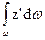обратим внимание на то, что подынтегральное выражение можно рассматривать как статический момент площадки dω относительно координатной оси 0 х (или оси 0 х'). Тогда этот интеграл представит собой сумму статических моментов элементов площади ω, т. е. статический момент самой площади 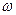относительно той же оси 0 х.

Известно, что статический момент площади относительно любой оси, лежащей в той же плоскости, равен произведению этой площади на расстояние от центра ее тяжести до оси моментов.

Таким образом,

,

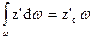где z'_c – расстояние от точки с (центра тяжести площади ω) до оси 0 х́ (оси моментов).

Делая соответствующие подстановки в формулу (70), получим

P 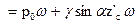. (71)

Здесь первое слагаемое р₀ω представляет собой атмосферное давление на свободную поверхность, передаваемое жидкостью по закону Паскаля, а второе — давление, оказываемое на стенку уже самой жидкостью (можно сказать — избыточное давление).

Перепишем формулу (71) в более удобном для практических расчетов виде. Заметим, что произведение z'_c sin α равно глубине погружения центра тяжести площади ω под уровень свободной поверхности h_с, поэтому

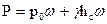, (72)

или, за вычетом атмосферного давления,

. (73)

Произведение h_сω представляет собой объем цилиндра с площадью основания, равной 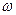, и высотой, равной h_c, с учетом чего формулу (73) можно прочитать так: сила, с которой жидкость действует на плоскую стенку, равна весу жидкости в объеме цилиндра с основанием, равным площади данной стенки, и высотой, равной глубине погружения центра тяжести этой площади под уровень свободной поверхности.

Дата добавления: 2014-12-26